前一篇介紹了Linear Regression的相關用法，也提到了在Linear Regression之中我們要藉由最小化所有資料點的誤差，來找到迴歸線。因此這一篇要介紹Gradient Descent，藉由此方法來找尋最佳解。

Gradient Descent(梯度下降法)

梯度下降法是一種最佳化方法，最佳化方法大概可以想像是一種求極值類型的題目，比較通用的就是在求最大值、最小值、最短路徑等等，梯度下降法被廣泛使用在機器學習的演算法之中，像是Linear Regression、Logistic Regression與Neural networks之中都有所使用。

梯度下降法的求解是利用偏微分的斜率，在一次一次慢慢地迭代之中，下降到最低點。有個隔壁棚的學長跟我說過，梯度下降法就像是在下山，先走一步後看看此處有沒有比較矮，若有就繼續往前走一步，沒有則倒退，藉由這樣慢慢地走到山谷。

以數學的方式來講，梯度下降法首先需要一個函式，假設我們的函式使用
這個函式就是我們的目標函式，我們的目標是找到這個函式的最小值，意旨著要找到一個x帶進去這個函式會得到最小值，這個函式會長成這樣。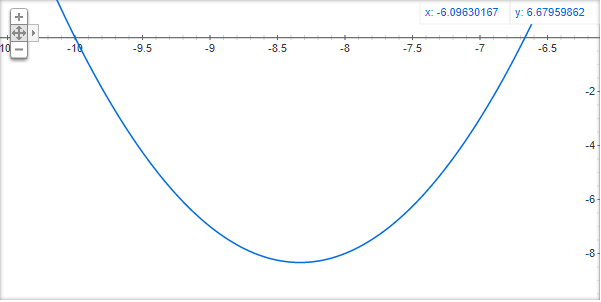

再來將這個函式對x做微分，得到函式，微分後的意義代表的是目標函式在那個點的斜率，寫成程式碼會長成這樣

double target(double x) {
	return 6 * x + 50;
}

在實作梯度下降法之前，我們還需要指定一個參數，叫做Learning Rate(學習率r)，影響梯度下降的速度，以爬山的例子來講就是影響一步走多遠的參數，如果Learning Rate過大，很容易會一步就跨過山谷略過最小值，但太小的話又會需要大量的步數來找到答案，因此Learning Rate的決定也是一門學問(對我個人來講就是trial and error)。

接著我們就可以開始做梯度下降法，梯度下降法是依照這個公式不斷的去做迭代

	double learningRate = 0.03;
	double num = 42;
	double nextNum;

	for (int i = 0; i < 1000; i++) {
		nextNum = num - learningRate * target(num);
		num = nextNum;
	}

	cout << "minimum = " << num << "\n";
	return 0;

這邊因為想要簡化程式碼，直接指定迭代一千次，正常情況下使用while迴圈檢查num與nextNum的變化量，若已不再變化或變化量很小代表已經迭代到最佳解。沒錯，梯度下降法的概念就是那麼簡單。

程式最後的輸出為-8.33333

這個函式很簡單，我們可以用微積分的方式，微分之後斜率等於0的地方，意旨6x=-50，則x=-8.333333333，與梯度下降法實作的結果相當。

參考資料：
Machine Learning學習日記 — Coursera篇 (Week 1.3):Parameter Learning, Gradient Descent For Linear Regression
Wikipedia-Gradient Descent
Gradient Descent: All You Need To Know