在Day3及Day4分別介紹了Linear Regression和Gradient Descent，那麼今天就是要把他們實作出來囉，首先先製作一個目標函式，由於是用線性迴歸，這邊就把目標函式設定成線性。

而上面的6與3就是我們需要迴歸而出的目標。

首先呢，因為迴歸需要資料，於是我們先把迴歸需要的資料做出來，先宣告一個函式，他會依照我們的目標函式生出相對應的值，並且賦予一個隨機性的誤差

double fun(double x) {

	double c = (double)rand() / RAND_MAX * 6 - 3;
	return x * 6 + 3 + c;
}

接著宣告一個函式，會隨機的在x為-10~10之間產生資料點，並分別將資料儲存於dataSetX和dataSetY兩個vector容器裡面，分別代表x與其相對應有誤差的f(x)

void prepareDataSet(
	vector<double>& dataSetX, 
	vector<double>& dataSetY, 
	const int numData
) {
	double ran;

	dataSetX.reserve(numData);
	dataSetY.reserve(numData);

	for (int i = 0; i < numData; i++) {
		ran = (double)rand() / RAND_MAX * 20 - 10;

		dataSetX.push_back(ran);
		dataSetY.push_back(fun(ran));
	}
}

目前的主程式長的這個樣子

int main() {

	const int NUMDATA = 1000;

	//srand(time(NULL));
	srand(1);

	vector<double> dataSetX;
	vector<double> dataSetY;

	prepareDataSet(dataSetX, dataSetY, NUMDATA);

	return 0;
}

接著我們利用線性迴歸的概念，要找到一條線性方程式 t(x)=ax+b，這條線性方程式與上面亂數生產的一千個資料點的距離平方總和為最小值，意思就是我們要找到一個a與b，把dataSetX裡所有點位的x帶進這個方程式，並與dataSetY的誤差平方和要為最小值。

用數學函示來表達會長成這樣，除以n是為了取得平均的誤差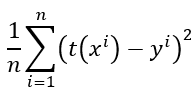

或者說我們把t(x)展開，會變成這樣：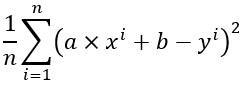

那要怎麼找到最小值呢，我們就要利用前面講了很多的Gradient Descent，Gradient Descent需要將要最佳化的變數微分，因此我們對上面的式子中的a與b做偏微分，得到這兩個式子：
對a做偏微分：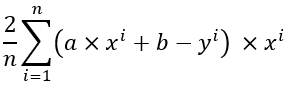

對b做偏微分：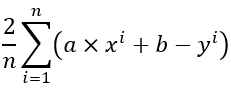

所以對於a與b做梯度下降的公式會變成：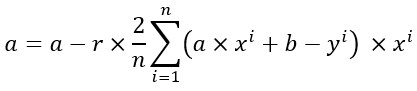

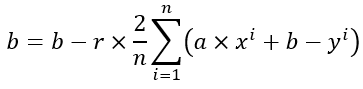
再來就是不斷迭帶上面那兩個函式然後求出最佳的a跟b囉，這邊是後續的程式碼：
在主程式新增Gradient Descent的學習率的參數，並且初始化a跟b(這邊直接帶0，亦可以用亂數的方式初始化)，呼叫gd這個函式並求得最佳的a與b。

int main() {

	const int NUMDATA = 1000;

	//srand(time(NULL));
	srand(1);

	vector<double> dataSetX;
	vector<double> dataSetY;

	prepareDataSet(dataSetX, dataSetY, NUMDATA);

	const double learnRate = 0.001;
	double a = 0, b = 0;

	gd(dataSetX, dataSetY, NUMDATA, a, b, learnRate);

	cout << "a -> " << a << endl;
	cout << "b -> " << b << endl;

	return 0;
}

而Gradient Descent函式的實作內容如下，只是把上述的數學式用程式碼實作出來而已，非常簡單且淺顯易懂：

void gd(
	vector<double>& dataSetX,
	vector<double>& dataSetY,
	const int numData,
	double &a,
	double &b,
	double learningRate
) {
	double totalA, totalB;
	double inversN = 1 / (double)numData;

	for (int iter = 0; iter < 10000; iter++) {
		totalA = 0; 
		totalB = 0;

		for (int i = 0; i < numData; i++) {
			totalA += (a * dataSetX[i] + b - dataSetY[i]) * dataSetX[i];
			totalB += (a * dataSetX[i] + b - dataSetY[i]);
		}

		a = a - learningRate * 2 * inversN * totalA;
		b = b - learningRate * 2 * inversN * totalB;
	}
}

跑出來的結果會受到學習率、迭帶次數以及一開始亂數產生的的所影響，因為問題頗為簡單，基本上都可以找到不錯的答案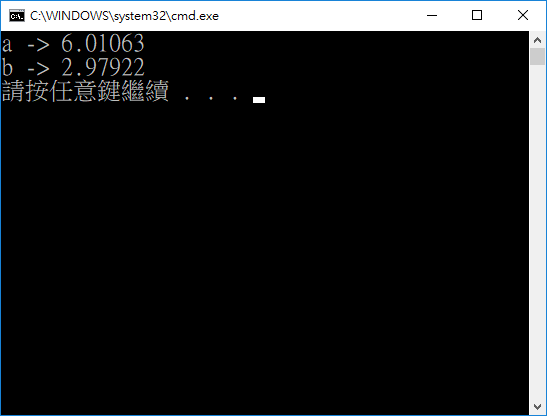

當初使用的公式f(x)=6x+3，而目前求出來的a為6.010，b是2.979，誤差感覺不算太大，以此證明這一次的Linear Regression是成功的!!!

參考資料：
Introduction to Machine Learning Algorithms: Linear Regression