今天終於要切入主題，開始探討機器學習的演算法，第一個演算法叫作Linear Regression，是一個在統計學常用的方法，而在Linear Regression之中會使用到梯度下降法(Gradient Descent)，也會一併於本章節介紹。

Linear Regression(線性迴歸)

我個人認為線性迴歸大概就像是機器學習裡面的Hello World，是一個非常基本，但又實用的方法，線性迴歸的原理很簡單，是以線性方程式為基礎，並且找到一條誤差最小的方程式。Excel裡面的趨勢線，就有使用線性迴歸所求得的。

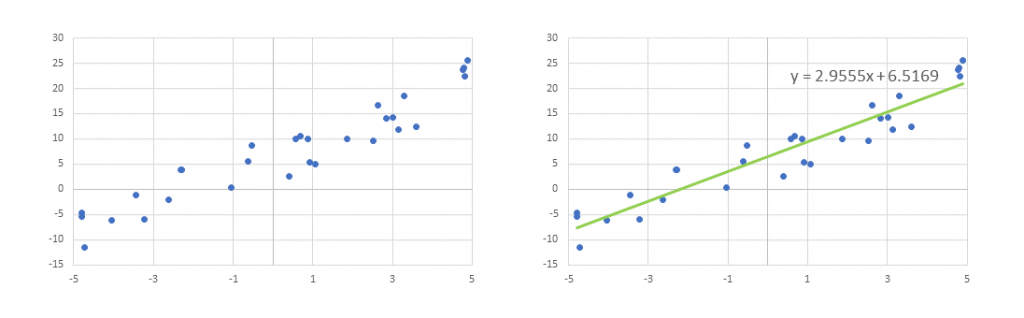
線性迴歸在機器學習裡面是屬於監督式的學習，因為在訓練的時候使用的資料是具有標籤。以上圖的案例來說，我是輸入了30個點的座標值，藉由30個點位的輸入(x)，以及輸出(y)，Excel求得了迴歸的結果 y = 2.9555x + 6.5169。

那線性迴歸是怎麼做到的呢，上述說要找到一條方程式，這條方程式對於所有的資料點位有著最小的誤差，換句話說就是要找到一條線，並且讓所有的點到這條線的距離總和是最小的，這些距離就是代表著迴歸線與資料點位的誤差，但因為誤差有正負號的差別，因此我們會將這個誤差平方後相加，作為誤差的總和。

好，那目前我們已經知道需要找到一條線，去最小化這條線與這些資料點的距離總和，國中數學有學過，最基本的線性函式為 y=ax+b，我們藉由調整a和b兩個值，去改變這條線的斜率和高度。因此，我們的問題就變成了一個最佳化的問題，藉由最佳化a與b兩個數字，目標是可以讓所有點位與方程式的距離是最短的。那既然是最佳化的問題，就可以用很多種方法去解，像是我很喜歡的超啟發式演算法、最佳化演算法等等，我在許多的機器學習文獻上面看到他們都會使用Gradient Descent(梯度下降法)作為找到迴歸問題最佳解的方法，因此在後續我會接著介紹梯度下降法。