評估模型

2019鐵人賽

catxxx519

2018-10-29 22:39:36

3058 瀏覽

分享至

評估模型

為了決定一個分類模型是否準確地捕捉了模式，我們必須評估該模型。評估的結果對於決定模型是多麼值得信賴以及我們如何使用它是非常重要。評估也可以是一個有效的工具，用於指導我們在未來改進模型。

測試集

注意少數標籤的數量

對於有少量平衡的標籤和一個多樣化的測試集的分類任務，只要100個評估實例就可以進行有意義的評估。
但是，如果一個分類任務有大量的標籤或包括非常罕見的標籤，那麼選擇的測試集的大小就要保證出現次數最少的標籤至少出現50次。

確保測試集獨立

如果測試集中出現來自於訓練集的資料，將高估模型的精度

注意樣本多樣性

測試集與訓練集的數據越相似輸出的精度就越可能被高估，也許模型只適合使用在這種類型的資料，例如評估東方股市指標的模型使用西方股市資料測試精度往往降低，因為訓練模型時就沒碰過西方數據

準確度

解釋一個分類器的準確性得分，考慮測試集中單個類標籤的頻率是很重要的。
我們在以色列判斷阿明95%是猶太人比起在美國判斷阿明95%是猶太人，一樣是95%但積極程度是不一樣的

精確度和召回率

我們給出一個答案後，一定會出現以下其中一種結果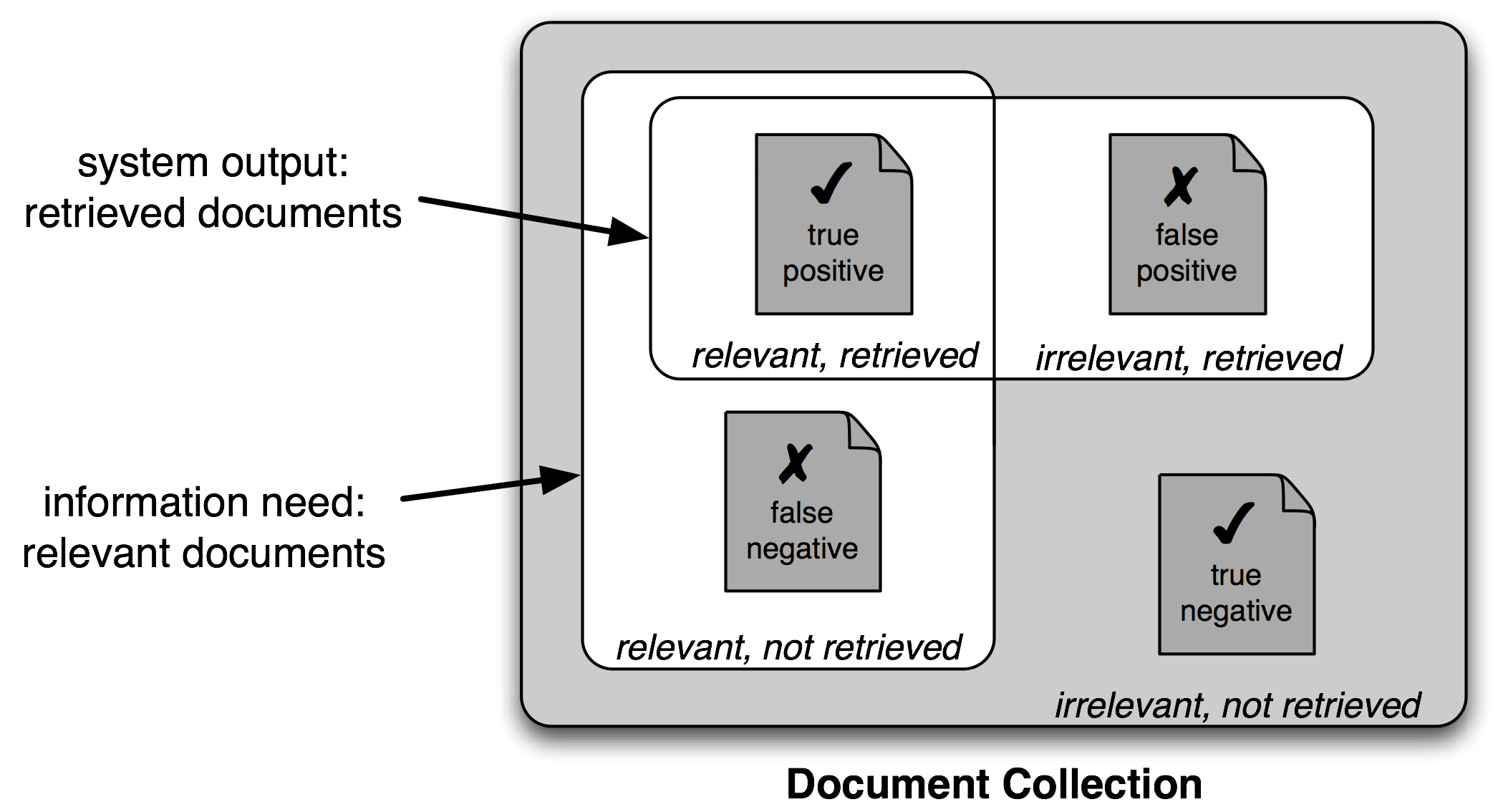

因此，對搜索任務使用不同的測量集是很常見的，基於上圖所示的四個類別的每一個中的項目的數量：

真陽性是相關項目中我們正確識別為相關的。
真陰性是不相關項目中我們正確識別為不相關的。
假陽性（或I型錯誤）是不相關項目中我們錯誤識別為相關的。
假陰性（或II型錯誤）是相關項目中我們錯誤識別為不相關的。
給定這四個數字，我們可以定義以下指標：

精確度，表示我們發現的項目中有多少是相關的，TP/(TP+FP)。
召回率，表示相關的項目中我們發現了多少，TP/(TP+FN)。
F-度量值（或F-Score），組合精確度和召回率為一個單獨的得分，被定義為精確度和召回率的調和平均數(2 × Precision × Recall ) / ( Precision + Recall )。

混淆矩陣

當處理有3個或更多的標籤的分類任務時，基於模型錯誤類型細分模型的錯誤是有信息量的。一個混淆矩陣是一個表，其中每個cells [ i , j ]表示正確的標籤i被預測為標籤j的次數。因此，對角線項目（即cells |ii|）表示正確預測的標籤，非對角線項目表示錯誤。在下面的例子中，我們為4中開發的一元標註器生成一個混淆矩陣：

     | N | | NIAJNVN | | NNTJ . S , BP | 
----+------------- -------------------------------------------------- -+ 
NN | <11.8%> 0.0% . 0.2% . 0.0% . 0.3% 0.0% | 
IN | 0.0% <9.0%> . . . 0.0% . . . | 
AT | . . <8.6%> . . . . . . | 
JJ | 1.7% . . <3.9%> . . . 0.0% 0.0% | 
  . | . . . . <4.8%> . . . . |
NNS | 1.5% . . . . <3.2%> . . 0.0% | 
  , | . . . . . . <4.4%> . . | 
VB | 0.9% . . 0.0% . . . <2.4%> . | 
NP | 1.0% . . 0.0% . . . . <1.8%>| 
----+----------------------------- -----------------------------------+ 
(row = reference; col = test)

交叉驗證

我們在使用太小的測試集測試模型時評價會不準確，但當測試集佔特徵集比例越大往往表示訓練集被縮小了。我們可以將現有的測試集分為N份，將這些測試集都去測試模型會得到N個評分，當這N個分數彼此相近差異不大那麼這個模型是較可信賴的。另一方面，如果N個訓練集上分數很大不同，那麼，我們應該對評估得分的準確性持懷疑態度。

常用模型原理

決策樹

決策樹是一個簡單的為輸入值選擇標籤的流程圖。這個流程圖由檢查特徵值的決策節點和分配標籤的葉節點組成。為輸入值選擇標籤，我們以流程圖的初始決策節點開始，稱為其根節點。此節點包含一個條件，檢查輸入值的特徵之一，基於該特徵的值選擇一個分支。沿著這個描述我們輸入值的分支，我們到達了一個新的決策節點，有一個關於輸入值的特徵的新的條件。我們繼續沿著每個節點的條件選擇的分支，直到到達葉節點，它為輸入值提供了一個標籤。

一旦我們選擇了一個特徵，就可以通過分配一個標籤給每個葉子，基於在訓練集中所選的例子的最頻繁的標籤，建立決策樹樁（即選擇特徵具有那個值的例子）。

熵和信息增益

正如之前提到的，有幾種方法來為決策樹樁確定最有信息量的特徵。一種流行的替代方法，被稱為信息增益，當我們用給定的特徵分割輸入值時，衡量它們變得更有序的程度。要衡量原始輸入值集合如何無序，我們計算它們的標籤的熵，如果輸入值的標籤非常不同，熵就高；如果輸入值的標籤都相同，熵就低。特別地，熵被定義為每個標籤的概率乘以那個標籤的log概率的總和：https://zh.wikipedia.org/wiki/%E7%86%B5_(%E4%BF%A1%E6%81%AF%E8%AE%BA)

import math
def  entropy (labels): 
   freqdist = nltk.FreqDist(labels) 
   probs = [freqdist.freq(l) for l in freqdist] 
   return -sum(p * math.log(p,2) for p in probs)

一旦我們已經計算了原始輸入值的標籤集的墒，就可以判斷應用了決策樹樁之後標籤會變得多麼有序。為了這樣做，我們計算每個決策樹樁的葉子的熵，利用這些葉子熵值的平均值（加權每片葉子的樣本數量）。信息增益等於原來的熵減去這個新的減少的熵。信息增益越高，將輸入值分為相關組的決策樹樁就越好，於是我們可以通過選擇具有最高信息增益的決策樹樁來建立決策樹。

決策樹強迫特徵按照一個特定的順序進行檢查，即使特徵可能是相對獨立的。例如，按主題分類文檔（如體育、汽車或謀殺之謎）時，特徵如hasword(football)極可能表示一個特定標籤，無論其他的特徵值是什麼。由於決策樹頂部附近的空間有限，大部分這些特徵將需要在樹中的許多不同的分支中重複。因為越往樹的下方，分支的數量成指數倍增長，重複量可能非常大。並且越往樹的下方，資料的數量越小使得決策樹處理增益訊息較小的標籤結果可能有問題

樸素貝葉斯分類器

在樸素貝葉斯分類器中，每個特徵都得到發言權，來確定哪個標籤應該被分配到一個給定的輸入值。為一個輸入值選擇標籤，樸素貝葉斯分類器以計算每個標籤的先驗概率開始，它由在訓練集上檢查每個標籤的頻率來確定。之後，每個特徵的貢獻與它的先驗概率組合，得到每個標籤的似然估計。似然估計最高的標籤會分配給輸入值。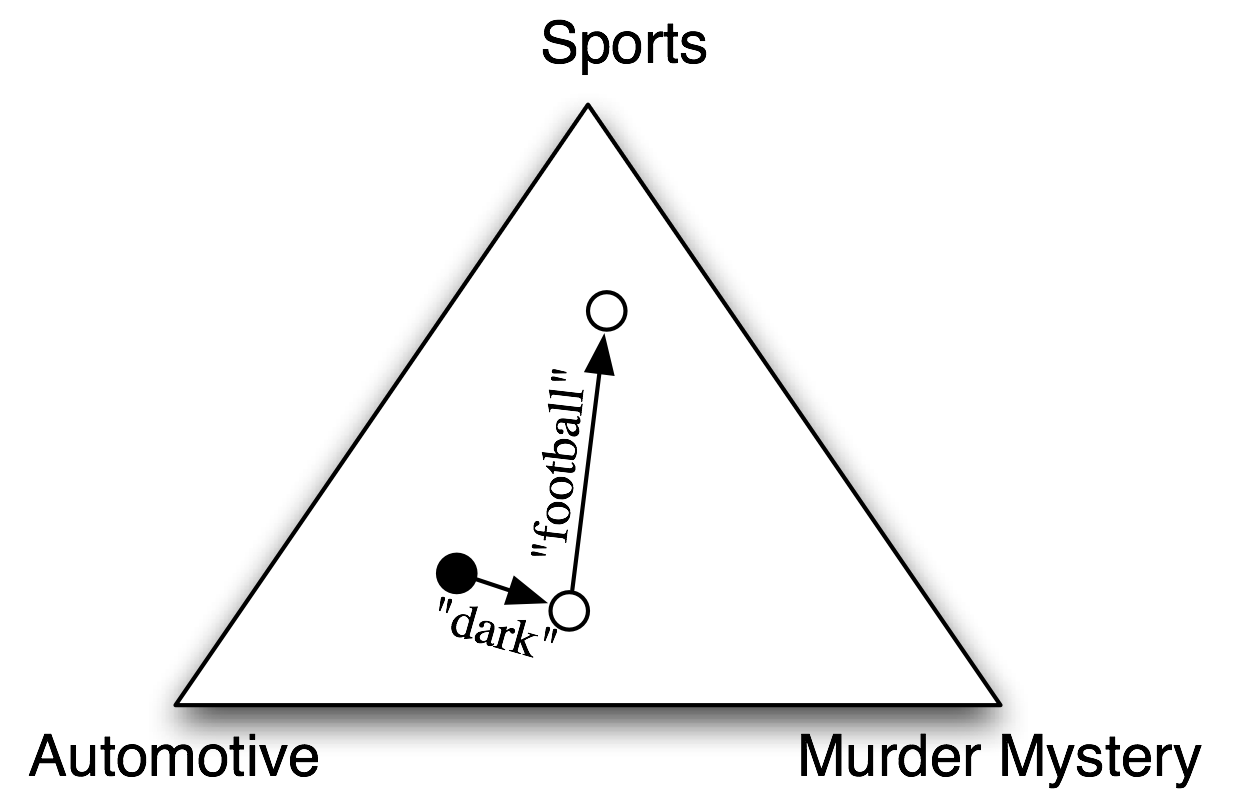

個別特徵對整體決策作出自己的貢獻，通過“投票反對”那些不經常出現的特徵的標籤。特別是，每個標籤的似然得分由於與輸入值具有此特徵的標籤的概率相乘而減小。例如，如果詞run在12%的體育文檔中出現，在10%的謀殺之謎的文檔中出現，在2％的汽車文檔中出現，那麼體育標籤的似然得分將被乘以0.12，謀殺之謎標籤將被乘以0.1，汽車標籤將被乘以0.02。整體效果是略高於體育標籤的得分的謀殺之謎標籤的得分會減少，而汽車標籤相對於其他兩個標籤會顯著減少。