要講機器學習，最基礎的理論來源應該就是線性迴歸(Linear Regression) 的求解方式，藉由簡易而古老的最佳化數學題目，用數值方式，以嶄新的梯度下降法，驗證可以藉由數據批量餵入模型中，讓系統自動【學習】到最佳參數解。

Fields一樣從Mxnet 教學網站 Deep Learning - The Straight Dope 以及动手学深度学习 取材。與其他機器學習教學一樣，以房價預測這個虛擬的問題來解釋所謂的單層神經網路。

模型定義

我們先定義變數：假設一棟房子成交價格為 ，它的面積為 ，屋齡為 。我們假設它們三者之間有線性關係，亦即 與 可以表達出 ，這種表達方式我們稱為房價預測的【模型(model)】。以線性迴歸模型來表述房價與 (面積，屋齡)關係為：

我們用 還有 兩個數值來當作權重 (Weight)，還有 這個數值當作偏差(Bias)， 這三個都叫做模型的參數(Parameter)
而 是模型輸出的房價預測值。這個值既然是預測出來的，我們如果餵入收集到的歷史數據，有很大的概率房價預測值與真實值是不太一樣的，後面的模型訓練目的就是要讓預測值與真實值趨近一致。

訓練模型

要訓練一個模型，必須先有數據。利用數據反覆的滾算出上述的參數，讓預測值越來越逼向真實值(誤差小)。這個過程有三個基本條件 :

一，訓練用數據集

當我們收集房價與(面積，屋齡) 這三者的數據後，這些資料被當作【訓練資料集(Training Dataset)】。 每一間房屋的資料就稱為【樣本(Sample)】，樣本應該有真實房價，被稱為【標籤 (Label)】；另外還有(面積，屋齡)兩個數據，我們用這兩個數據來預測房價， 因而被稱為【特徵值(feature)】。 以這種有帶【標籤 (Label)】的訓練資料集來進行模型訓練，一般稱之為【監督式學習(Supervised Learning)】

假設我們總共有 個樣本，第個樣本特徵分別為 與 ：那對應的標籤應為 ，那對應第 個房子，我們用線性迴歸模型所預測的房價為：

二，定義誤差的損失函數

我們經常用平方函數來當作誤差的損失函數，除了它能表達誤差越大，則損失值越大外，不會是負數，且簡單易算。

公式前方會出現一個常數1/2並不是重點，只是因為對該函數計算導數，會變成 2*(1/2) =1。計算可以少一次乘法(x2)。這只是其中一個樣本的損失，但是我們的目標是讓總損失最小，所以我們需要將全部樣本計算所有損失加總：

仔細看這個總損失函數我們能變動的只有 這三個數值(就是我們之前說的參數)。其他房價，面積，屋齡都是歷史數據的樣本值。

我們的目標；找到一組模型參數，我們標記為 來讓上述的總損失最小。搞演算法的總是要把這種想法變成像公式：

三，最佳化所用的演算法 mini-batch stochastic gradient descent

機器學習有一套常用的方法來幫忙找到上述的 。最常用可能是 mini-batch stochastic gradient descent，此算法的特點在：並不是一次把訓練集所有 n 筆帶入計算，這對許多實務上的大資料集，以現有的計算資源來講，是無法負荷的。所以改用迭代逐步尋找最佳解，方法如下：

1. 先隨機給予上述三個參數
2. 持續進行下面
   -從全部樣本隨機抽樣固定數量的樣本 (mini-Batch)
   -以此批量樣本的數據計算梯度（計算導數）
   -依梯度按照一定比例更新參數 （細節用下列公式來表達）

我們將上述虛擬碼寫成公式如下：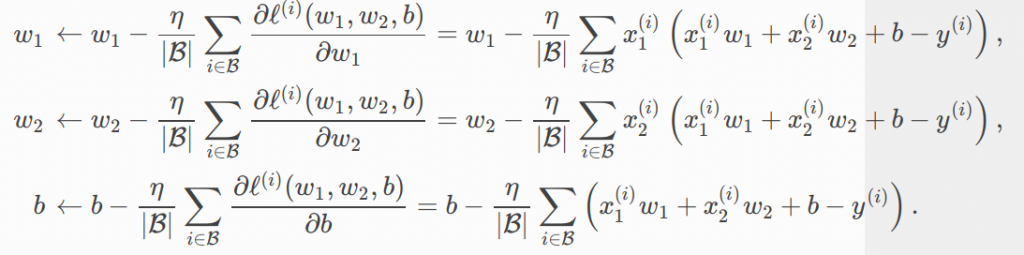

上面式子有三個等號，都是對下面這個損失函數（我們在之前定義的）做偏微分，是很基本的偏微分方程，懂一點數學的應該理解。不懂其實也沒關係，只要知道目的基本上就是要找到最快可以降低損失值的方向。

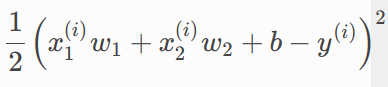
公式裡還有幾樣事要留意：

1. 是miniBatch 的個數
2. 稱之為學習率 (Learning Rate)。當找到方向後，還要決定一次走多遠，這個由此數值決定

這兩個數值並不是模型計算中會幫忙找出來的，是訓練此模型的人（訓練師）要決定的，所以被稱為『超參數（hyper parameter）』，我們未來訓練過程，常需要一直找合適的超參數，有人把這過程簡稱叫做『調參』。

備註：

專案緣起記錄在 【UP, Scrum 與 AI專案】