前言

梯度下降法（Gradient Descent Algorithm）是一個一階最佳化算法，通常也稱為最速下降法。 要使用梯度下降法找到一個函數的局部極小值，必須向函數上當前點對應梯度（或者是近似梯度）的反方向的規定步長距離點進行疊代搜索[1]。

說明

梯度下降是找到函數最小值的一種方法。在神經網絡的情況下，我們想要最小化的功能是成本函數。梯度下降通過調整網絡參數來實現，這樣我們從成本函數中獲得的值比以前更低。從某種意義上說，梯度下降盡可能“下坡”，就像螞蟻感覺到地形的斜坡一樣。每當它向下移動時，梯度下降通過更新每個神經元中的權重和偏差來“節省”其進度。最終，梯度下降將找到成本函數的最底層[2]。
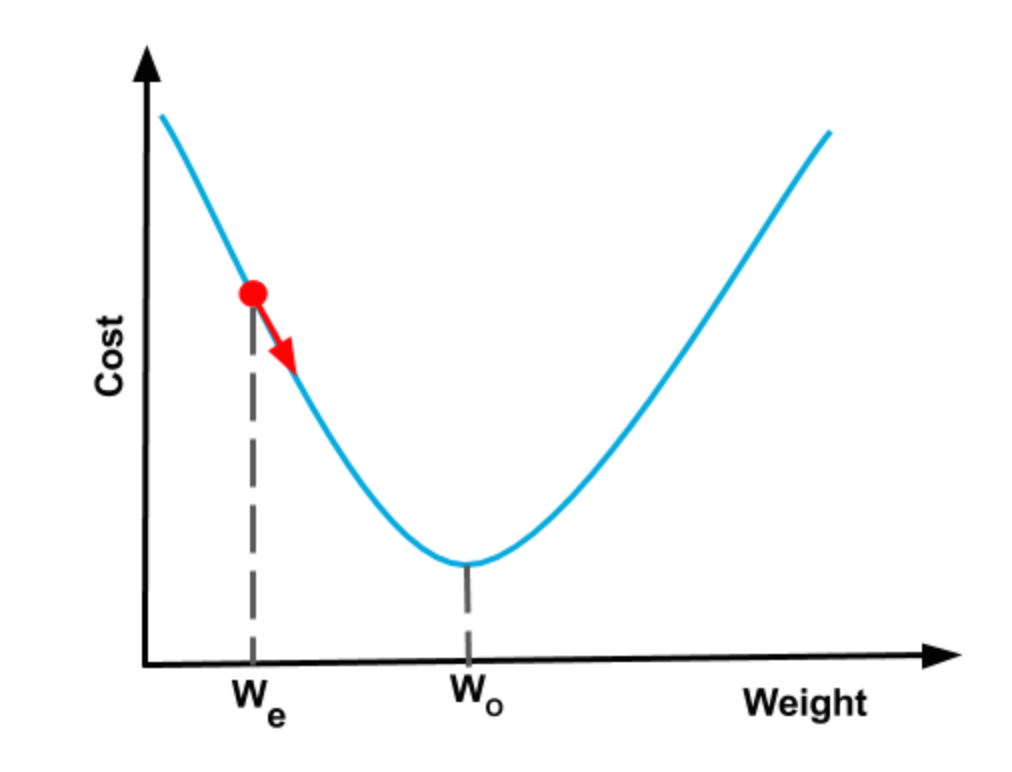
如下圖，讓我們回到我們的神經網絡，只需一個旋鈕，機器學習術語中，這些“旋鈕”被稱為神經網絡的參數。如果我們將這些旋鈕調到正確的位置，那麼對於任何輸入我們都可以得到我們想要的輸出。並假設我們當前對旋鈕設置（或重量）的估計是 We。 如果我們的成本函數形狀像一個碗，我們可以找到成本函數的斜率，並更接近最佳旋鈕設置Wo。 此過程稱為漸變下降，因為我們基於斜率（漸變）向下移動（下降）曲線。當您到達碗的底部時，坡度或坡度變為零，這樣就完成了訓練。 這些碗狀功能在技術上稱為凸函數。

參考

1.梯度下降法（Gradient descent）@維基百科
2.機器學習@Berkeley