前言

昨天用算術收益率來介紹夏普指數(Sharpe ratio)，今天要用更貼近金融的對數收益率來算出夏普指數。

預先載入套件

介紹底下的圖表之前先預先載入需要的套件

# basic
import numpy as np
import pandas as pd

# get data
import pandas_datareader as pdr

# visual
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns

#time
import datetime as datetime

讀取股票

我們讀取以下股票
2330：台積電
2492：華新科
3045：台灣大
2412：中華電

start = datetime.datetime(2015,1,5)
df_2330 = pdr.DataReader('2330.TW', 'yahoo', start=start)
df_2492 = pdr.DataReader('2492.TW', 'yahoo', start=start)
df_3045 = pdr.DataReader('3045.TW', 'yahoo', start=start)
df_2412 = pdr.DataReader('2412.TW', 'yahoo', start=start)

股票間的比較

• 結合四個股票

df_total = pd.concat([df_2330['Adj Close'],df_2492['Adj Close'],df_3045['Adj Close'],df_2412['Adj Close']], axis=1)
df_total.columns=['2330', '2492', '3045', '2412']

• 日收益率平均

df_total.pct_change().mean()

# 輸出結果
2330    0.000663
2492    0.003169
3045    0.000090
2412    0.000356
dtype: float64

• 日收益率相關分析

df_total.pct_change().corr()

# 輸出結果
	        2330	    2492	    3045	    2412
2330	1.000000	0.181331	0.224544	0.318880
2492	0.181331	1.000000	0.086055	0.067629
3045	0.224544	0.086055	1.000000	0.333560
2412	0.318880	0.067629	0.333560	1.000000

相關分析這邊指的是研究兩個或兩個以上隨機變亮之間相互依存關係的方向和密切程度的方法。
如果用r表示相關程度。
r > 0 線性正相關。
r < 0 線性負相關。
r = 0 兩個變量之間不存在線性關係。
r數值的相關性如下

因此可以看到台積電(2330)和中華電(2412)是中度相關，中華電(2412)和台灣大(3045)也是中度相關，其他都是低度相關

幾何收益率(對數收益率)和算術平均收益率

• 算術平均收益率(arithmetic return)

df_total.pct_change().head()
# pct_change()：(df_total[0] - df_total[1]) / df_total[1]

• 幾何收益率(對數收益率)(log return)
  假設初期投資1元，第一次結算價值(1+R1)元，第二期再用(1+R1)做投資，第二級結算就為(1+R1)(1+R2)元...以此類推，幾何平均收益率加上了複利的想法所以優於算術平均收益率。

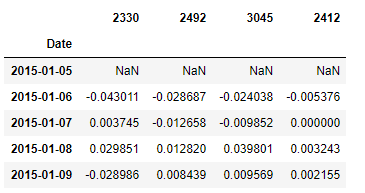
log_ret = np.log(df_total/df_total.shift(1))
#np.log() 以自然數e為基底
#df.shift() shift對數據進行位移的動作

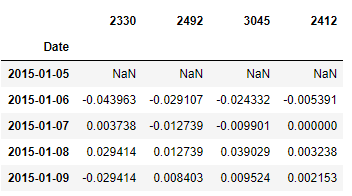
從兩張圖可以看到算術平均收益率和幾何平均收益率是非常相近的

畫出對數收益率的直方圖

plt.rcParams['axes.unicode_minus']=False
log_ret.hist(bins=100, figsize=(12, 8))

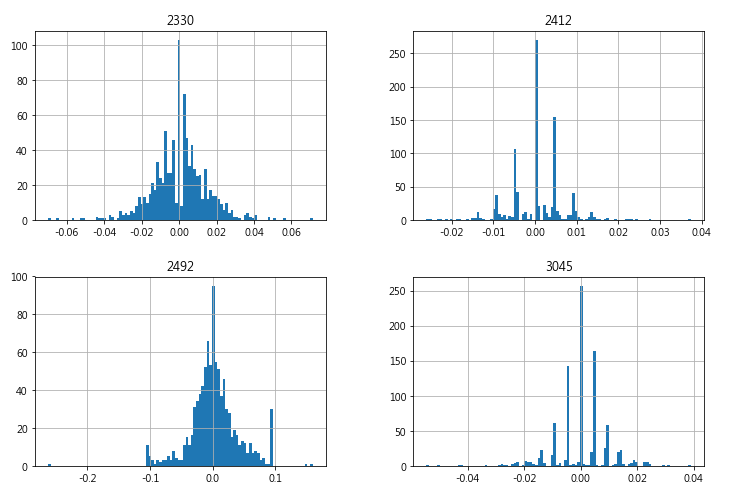
從上面四張圖可以兩兩比較每個股票收益率

• 對數收益率平均

log_ret.mean()

# 輸出結果
2330    0.000557
2492    0.002445
3045    0.000045
2412    0.000334
dtype: float64

• 對數收益率共變異數(協方差)(pairwise Covariance)
  共變異數用兩表示兩個隨機變量x,Y的相關性，如果共變異數為正，則代表X,Y同向變化，共變異數為負，則說明X,Y反向運動。絕對值的共變異數越大則越相關。
  公式：

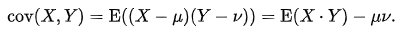
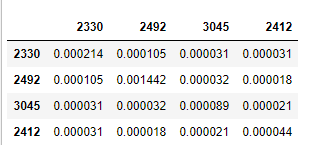
log_ret.cov()

用協方差來算出夏普指數(Sharpe ratio)

我們將我們的投資金額用以下的比例分配
2330：台積電 30%
2492：華新科 20%
3045：台灣大 25%
2412：中華電 25%

• 股票投資比重

weight = np.array([0.3, 0.2, 0.25, 0.25])
print('股票投資比重--->', weight)

• 平均日收益率
  使用對數收益率的平均乘上比重(weight)再乘上交易日(252)

exp_ret = np.sum((log_ret.mean() * weight )* 252)
print('投資組合的預期報酬--->', exp_ret)

• 波動性(expected volatility)
  夏普指數的分母(denominator)

exp_vol = np.sqrt(np.dot(weight.T, np.dot(log_ret.cov()*252, weight)))
print('預期波動性--->',exp_vol)

np.dot：矩陣乘法，等同線性代數中乘法，用以下的例子解釋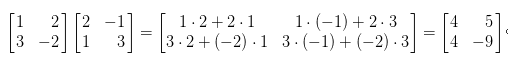

np.sqrt：矩陣開根號

• 夏普指數(Sharpe ratio)

SR = exp_ret/exp_vol
print('夏普指數--->', SR)

# 輸出結果
股票投資比重---> [0.3  0.2  0.25 0.25]
投資組合的預期報酬---> 0.18986638440106773
預期波動性---> 0.17017725257437183
夏普指數---> 1.115697788798719

參考網站

綠角財經筆記：標準差怎麼算

之前的章節

• 安裝環境
  • 安裝Anaconda
  • 安裝Jupyter notebook
• 股票
  • 介紹股票
  • 抓取股票
  • 基本分析
  • 繪製K線圖
  • 財報爬蟲和分析
  • 投資組合的風險評估 - 算術平均數
• 程式碼位置
  • github
    因為作者本身也是第一次學習Python和寫程式文章，也是才碰股票沒幾天而已，所以編排上會有點亂，觀念可能也會錯誤，如果有疑問可以提出一起討論。