Day 9 : 線性規劃問題(linear programming problem)

第 11 屆 iThome 鐵人賽

DAY 9

AI & Data

連接數學與現實世界的橋樑 -- 數學建模系列第 9 篇

11th鐵人賽 linear programming problem

spidyjames

2019-09-10 22:08:23

4469 瀏覽

分享至

當一個問題被視為凸性規劃問題，那其解就是全域最佳解，因此我們會希望手邊的問題是凸性規劃問題。今天要介紹的線性規劃問題就是凸性規劃問題的一種。

線性規劃問題是指，目標函數與限制條件都是線性的。線性規劃在理論上趨於成熟，尤其是可以將其轉換成矩陣型式，利用電腦來計算求解，因而實用性日益廣泛與深入。

基本概念

假如一個線性規劃問題存在最佳解，則該最佳解為全域最佳解。
呈1，線性規劃問題的最佳解必將出現在feasible set的邊界上或邊界的頂點上。

範例

(請先忽略原始問題如何轉換成標準LP型式，將焦點著重在解的特性，後續會再講解如何轉換)
原始LP問題:
$min f = -400x_1 - 600x_2$
s.t.
$x_1 + x_2 \le 16$
$https://chart.googleapis.com/chart?cht=tx&chl=%5Cfrac%7B1%7D%7B28%7Dx_1%20%2B%20%5Cfrac%7B1%7D%7B14%7Dx_2%20%5Cle%201$
$https://chart.googleapis.com/chart?cht=tx&chl=%5Cfrac%7B1%7D%7B14%7Dx_1%20%2B%20%5Cfrac%7B1%7D%7B24%7Dx_2%20%5Cle%2011$
$x_1, x_2 \ge 0$
轉成標準型式
$min f = -400x_1 - 600x_2$
s.t.
$x_1 + x_2 + x_3 = 16$
$https://chart.googleapis.com/chart?cht=tx&chl=%5Cfrac%7B1%7D%7B28%7Dx_1%20%2B%20%5Cfrac%7B1%7D%7B14%7Dx_2%20%2B%20x_4%20%3D%201$
$https://chart.googleapis.com/chart?cht=tx&chl=%5Cfrac%7B1%7D%7B14%7Dx_1%20%2B%20%5Cfrac%7B1%7D%7B24%7Dx_2%20%2B%20x_5%20%3D%2011$
$x_i \ge 0, i=1, \dots, 5$
解聯立，並將 $x_1, x_2$ 視為獨立變數，得通解為，
$x_3 = 16 - x_1 - x_2$
$https://chart.googleapis.com/chart?cht=tx&chl=x_4%20%3D%201%20-%20%5Cfrac%7B1%7D%7B28%7Dx_1%20%2B%20%5Cfrac%7B1%7D%7B14%7Dx_2$
$https://chart.googleapis.com/chart?cht=tx&chl=x_5%20%3D%201%20-%20%5Cfrac%7B1%7D%7B14%7Dx_1%20%2B%20%5Cfrac%7B1%7D%7B24%7Dx_2$
對LP問題的處理採用特殊的程序，即令 $p = n - m$ 個變數為0，則可由現有的m個方程式解n個變數。由此程序所得之解稱為，基本解。

以本題為例，
$n = 5$ , $m = 3 \Rightarrow p = 5 - 3 = 2$
若令 $x_1 = x_2 = 0 \Rightarrow x_3 = 16$ , $x_4 = 1$ , $x_5 = 1 \rightarrow A$
若令 $x_1 = x_4 = 0 \Rightarrow x_2 = 14$ , $x_3 = 2$ , $https://chart.googleapis.com/chart?cht=tx&chl=x_5%20%3D%20%5Cfrac%7B5%7D%7B15%7D%20%5Crightarrow%20E$
若令 $x_1 = x_3 = 0 \Rightarrow x_2 = 16$ , $https://chart.googleapis.com/chart?cht=tx&chl=x_4%20%3D%20%5Cfrac%7B-2%7D%7B7%7D$ , $https://chart.googleapis.com/chart?cht=tx&chl=x_5%20%3D%20%5Cfrac%7B1%7D%7B3%7D%20%5Crightarrow%20F$ (infeasible)
$\Rightarrow$ 基本解的數目為C5取2 = 10組

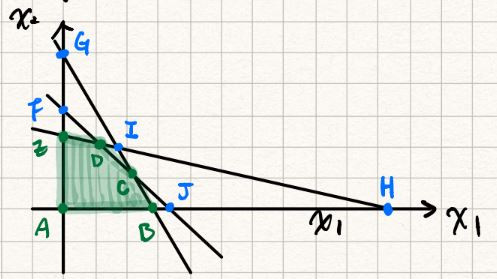
凸多邊形ABCDE之邊界及其內部為可行解區域，D為最佳解。
10組基本解對應到，
1. A,B,C,D,E之五個頂點為基本可行解
2. F,G,H,I,J之五個點為基本不可行解