我們在前面談了一堆求最佳解的條件與解法，但其實真正的最佳解"有可能"一直沒有被找到，這是甚麼意思。最佳解有兩種，一種是區域最佳解，另一種是全域最佳解，用白話一點的說法就是，班上的第一名(區域最佳解)未必是全校第一名(全域最佳解)。那為什麼我們要花時間在學習求區域最佳解，因為"有些情況"無法求得全域最佳解，只能退而求其次，而且取得區域最佳解已經可以滿足目標了。但是，還是有一些情況是可以解得全域最佳解，只要函數被判定為凸函數。

凸函數的一個重要性質，也就是可以由局部信息推導出全域信息。在數學分析中，我們大都是分析函數的局部信息(微分)，以此分析函數特性，而凸函數的特性可使我們只需分析函數的局部性質就可以獲知全局特性。因此，接下來幾天我們圍繞在凸函數上。

凸集合

若為凸集合 內之任意2點之連接線段上的所有點也在內。

凸函數

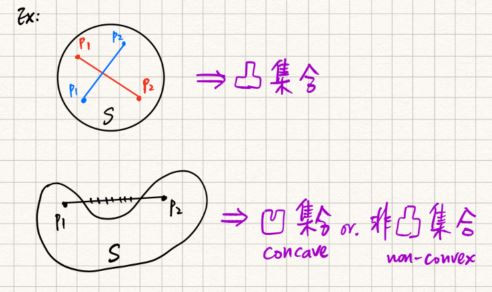
先複習一下，線段之參數式:
* 單變數: ;
* 多變數:
當,
當,

凸函數必須定義在凸集合上，其充要條件為，

• 單變數函數:
  ;
• 多變數函數:
  

檢驗函數的凸性(convexity)

由定義來下手，
在凸集合上之函數為凸函數 在內之所有點的皆為正定或半正定

範例

凸性規劃問題

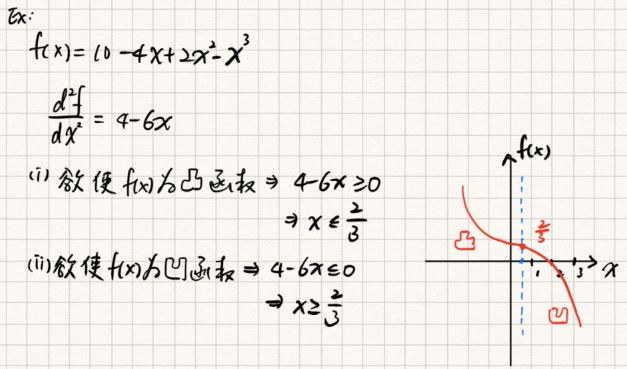
由等式限制條件 , 與不等式限制條件 , 所定義之Constraint set(a feasible set)

1. 如所有為線性函數，且為凸函數，則為凸集合
2. 如所有與皆為線性函數，則為凸集合
3. 如任何一個為非線性函數，則 S為非凸集合

若一個最佳化問題的為凸集合，且目標函數在內也為凸函數，則此最佳化問題屬於凸性規劃問題。其好處為，前述的KKT必要條件，可以同時為充分條件且找到的區域最小值即為全域最小值。

範例