Day 12 : 無限制條件之非線性規劃問題

第 11 屆 iThome 鐵人賽

DAY 12

AI & Data

連接數學與現實世界的橋樑 -- 數學建模系列第 12 篇

11th鐵人賽

spidyjames

2019-09-13 23:57:47

1668 瀏覽

分享至

今天我們將討論非線性規劃問題，這類問題更接近實際物理世界，缺乏較好的一般性方法，也就是說，每一個問題都是"客製化"的，也因此就算想用非常複雜的一般化方法來建立模型供大量情境使用也是很難的。

接下來幾天我們會從無限制條件的問題出發，並介紹一些相關的數值方法，然後就結束最佳化模型這個主題。

General algorithm

求解的基本概念

利用搜尋的方式逐步找到最佳解
$\bar X^{(k+1)} = \bar X^{(k)} + \Delta \bar X^{(k)}$
$k=0, 1, 2, \dots$ (遞迴次數)
以分量表示，
$x_{i}^{(k+1)} = x_{i}^{(k)} + \Delta x_{i}^{(k)}$
$i=1, \dots , n$ (設計變數的數目)
$\bar X^{(0)}$ : 代表數值法的起始點，通常會以合理猜測來取得。
$\Delta \bar X^{(k)}$ : 當前設計變數 $\bar X^{(k)}$ 之改變量

$\Delta \bar X^{(k)}$ 可以分解成兩個部分 $\Rightarrow \Delta \bar X^{(k)} = \alpha_k \bar d^{(k)}$ , $\alpha_k > 0$
$\alpha_k$ : 決定在 $\bar d^{(k)}$ 方向的最佳步長
$\bar d^{(k)}$ : 決定搜尋的方向

演算法步驟

評估與給定一合理的起始點 $\bar X^{(0)}$ ，令 $k = 0$
檢查演算法是否滿足終止條件，是的話停止運算，否的話則繼續。
計算下一搜尋方向 $\bar d^{(k)}$
在 $\bar d^{(k)}$ 方向上計算最佳步長 $\alpha_k$ , $\alpha_k > 0$
更新設計變數 $\bar X^{(k+1)} = \bar X^{(k)} + \alpha_k \bar d^{(k)}$ ，令 $k = k + 1$ ，回到步驟2

descent direction( $\bar d$ )的判斷

令 $\bar C^{(k)} = \nabla f(\bar X^{(k)})$ ，則 $\bar d^{(k)}$ 必須滿足， $\bar C^{(k)} \bar d^{(k)} < 0$
ex:
檢驗在點(0, 0)，方向 $\bar d = (1, 2)$ 是否為 $f(\bar X) = x_{1}^{2} - x_{1}x_{2} + 2x_{2}^{2} - 2x_{1} + e^{(x_{1} + x_{2})}$ 之descent direction
[sol]:
$\nabla f = \left [ \begin{array}{ll} 2x_{1} - x_{2} - 2 + e^{(x_{1} + x_{2})} \\ -x_{1} + 4x_{2} + e^{(x_{1} + x_{2})} \end{array} \right ] \Rightarrow \nabla f(0, 0) = \bar {C} (0,0) = (-1, 1)$
$\bar C \cdot \bar d = (-1, 1) \cdot (1, 2) = 1 > 0$
故 $\bar d$ 不是descent direction

求解descent step( $\alpha_k$ )

解析法
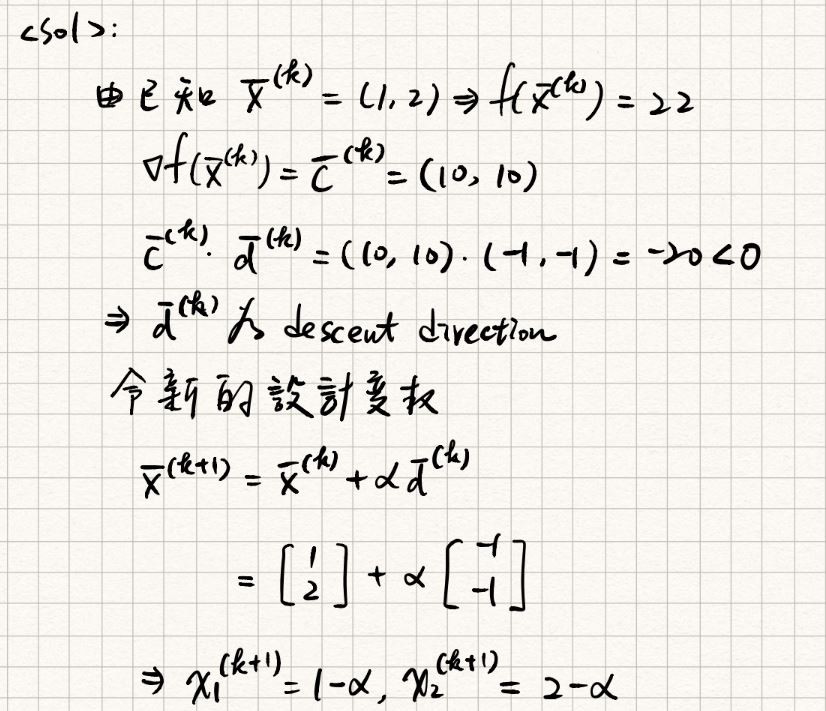
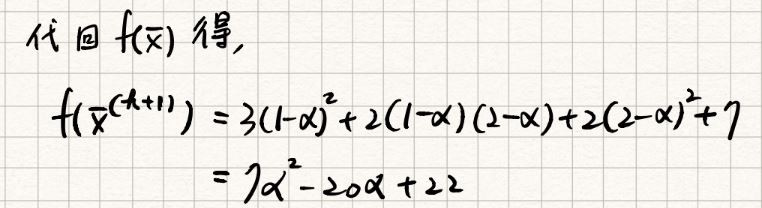
數值法
前提條件與概念

單峰函數(unimodal function)
一般情況而言，需先進行"劃界"(註1)，以確定函數在 $[a, b]$ 為單峰。
不確定區間(interval of uncertainty)
$I = \alpha_u - \alpha_l$ $\equiv$ $\alpha$ 的上限 - $\alpha$ 的下限
大部分的一維搜尋法經由迭代持續縮小 $I$ ，直到 $I < \epsilon$ (收斂參數)。此時， $https://chart.googleapis.com/chart?cht=tx&chl=%5Calpha%5E%7B%5Cast%7D%20%3D%20%5Cfrac%7B%5Calpha_l%20%2B%20%5Calpha_u%7D%7B2%7D$ ，以此方程式找到 $\alpha^{\ast}$ ，稱為Interval reducing method