Day 11 : 單形法(simplex method)的概念與解題步驟

第 11 屆 iThome 鐵人賽

DAY 11

AI & Data

連接數學與現實世界的橋樑 -- 數學建模系列第 11 篇

11th鐵人賽單形法

spidyjames

2019-09-12 23:57:51

23870 瀏覽

分享至

單形法是Danzig教授在二次大戰時發展出來，基本上是以LP問題的幾何特性，配合聯立方程組與高斯喬登消去法，可以求出LP的最佳解。

定理

對任一LP問題，其可行解所成之集合為凸集合，該凸集合之頂點對應到基本可行解
令大小為mxn的係數矩陣 $\bar A$ 具有全列數秩(full row rank)，即 $rank(\bar A) = m$ ，則

若存在一個可行解，則存在一個基本可行解
若存在一個最佳可行解，則存在一個最佳基本可行解

在求解 LP 時不必把全部的可行端點找出來，只要搜尋到下一個端點比目前的端點好，持續搜尋就保證可以找到整體最佳解，而不會只找到局部最佳解。

正準型式(Cononical form)

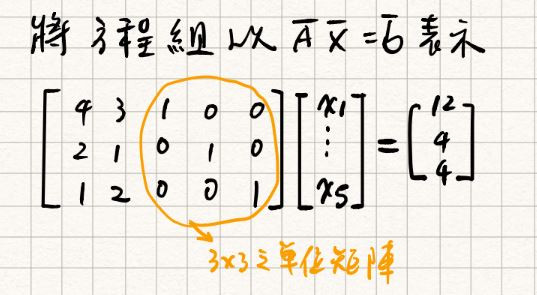
求解 $\bar A \bar X = \bar b$ 之前，先將其整理為正準型式，如下:
$\bar I_{(m)} \bar X_{(m)} + \bar Q \bar X_{(n-m)} = \bar b$ or $\bar X_{(m)} + \bar Q \bar X_{(n-m)} = \bar b$
其中， $\bar I_{(m)}$ 為mxm之單位矩陣
$\Rightarrow$ 可得 $\bar A \bar X = \bar b$ 之通解為 $\bar X_{(m)} = \bar b - \bar Q \bar X_{(n-m)}$
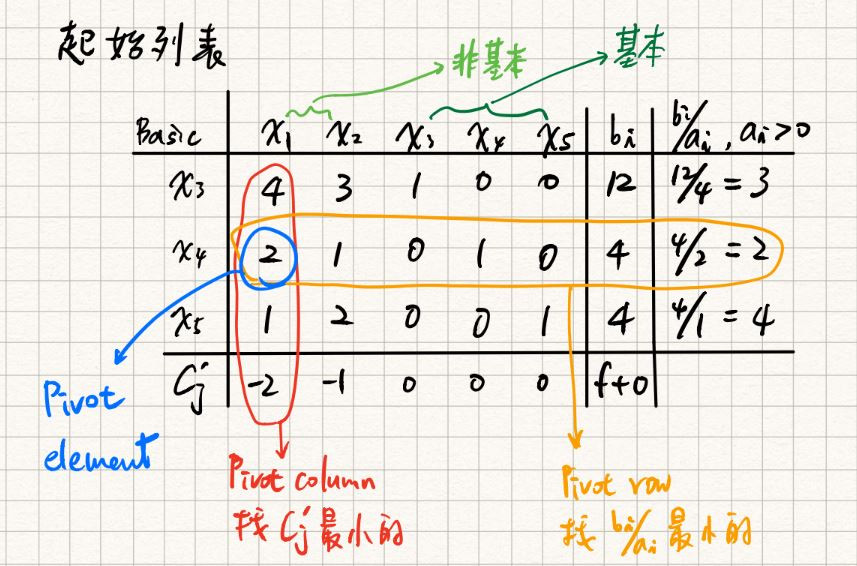
上式若設定非基變數 $\bar X_{(n-m)} = \bar 0$ (零向量) $\Rightarrow$ 可得基解為 $\bar X_{(m)} = \bar b$
如右側之 $b_i \ge 0$ ，則該基解即為基本可行解。

對於"基"的理解，可以把它當作是線性代數中的基底，而基變數就是基所對應的變數。

Pivot step

將基變數與非基變數互相交換的過程，稱為Pivot step。
Pivot column $\rightarrow$ Pivot row $\rightarrow$ Pivot element

範例

上述講了一堆，我們還是直接從範例來解釋求解過程。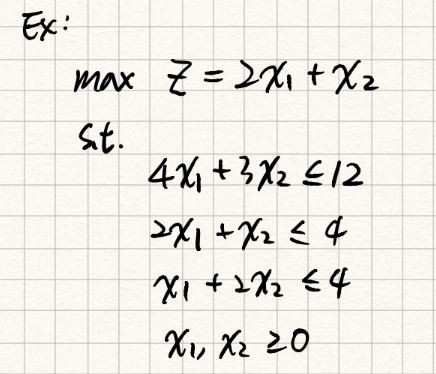

(i) simplex method的基本要求之一就是，將目標函數表示成非基變數的函數，而變數之前的係數稱為reduced cost coefficients，以符號 $C_{j}'$ 表式。以本例而言， $C_{1}' = -2$ , $C_{2}' = -1$
(ii) simplex method的啟動需要一組基可行解，以本例而言，非基變數: $x_{1} = 0$ , $x_{2} = 0$ 相當於圖解法中的A點(在可行區域內)，基變數: $x_{3} = 12$ , $x_{4} = 4$ , $x_{5} = 4$ ，目標函數值: $f = 0$

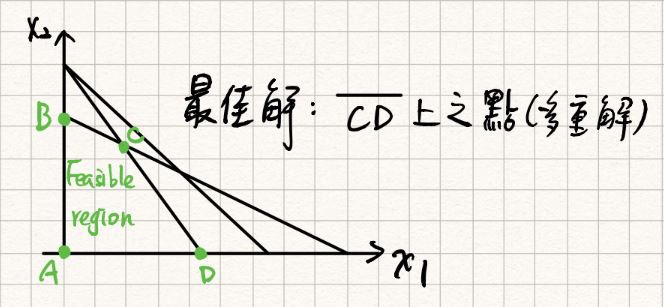
(iii) 最佳解檢驗，如對應非基變數之 $C_{j}' \ge 0$ ，且對應基變數之 $C_{j}' = 0$ ，則最佳解以求得。

經由基本列運算設法將Pivot element由2變成1，同行元素( $a_{11}$ 與 $a_{31}$ )變為0，同列元素跟著改變。另外，將 $C_{1}' = -2$ 變成 $C_{1}' = 0$ ，因為 $x_1$ 已變成基變數。
上表令 $x_2 = x_4 = 0$ ，得基解 $x_1 = 2$ , $x_3 = 4$ , $x_5 = 2$
其中( $x_1 = 2$ , $x_2 = 0$ )對應到D點為最佳基本可行解