前言

今天我們繼續新課程 Launching into Machine Learning 的第二章~

這幾天的文章會是一系列的，會需要一起看才比較能看懂整個ML模型的輪廓，
然而因為一天能寫的內容量有限，所以我會在前言部分稍微說明我寫到哪。

複習一下ML的整個訓練過程

因為ML模型的訓練階段章節內容會分很多部分，我們要先確認好自己在哪個階段，
以免吸收新內容卻不知道用在內容的什麼地方。

★ML的整個「訓練過程」：這裡以監督式學習(Supervised Learning)為例

Course - Launching into Machine Learning

第二章節的課程地圖：(紅字標記為本篇文章中會介紹到的章節)

• Practical ML
  • Introduction to Practical ML
    • Introduction
  • Supervised Learning
    • Supervised Learning
    • Regression and Classification
  • ML History
    • Short History of ML: Linear Regression
    • Short History of ML: Perceptron
    • Short History of ML: Neural Networks
    • Short History of ML: Decision Trees
    • Short History of ML: Kernel Methods
    • Short History of ML: Random Forests
    • Short History of ML: Modern Neural Networks
    • 討論提示: Modern Neural Networks
  • Module Quiz

Regression and Classification

課程地圖

• Practical ML
  • Supervised Learning
    • Regression and Classification

今天我們要來更細部的解說Regression與Classification的差別，昨天已經有先做簡單的比較了。

一樣先講結論，想看詳細說明或例子再往下拉吧~

不論是regression problem或classification problem，
皆是屬於監督式學習(Supervised Learning)的問題。

一樣的我們再整理一下：

Regression problem

一樣我們先從昨天的例子來看，
我們想從其他資訊features預測tip的價格
tip是我們的預測的目標，也就是我們的label
也因為tip是連續值，所以這是個regression problem。

在regression problem中，我們的目標是使用數學函數去組合不同的features，
這樣我們就能預測出一個連續值作為我們結果的label。

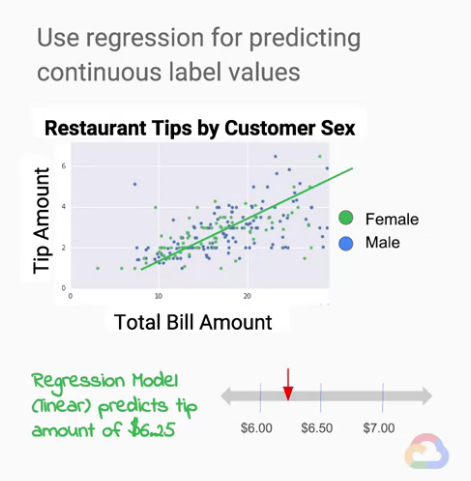
我們先稍微把問題簡化一下，假設現在只考慮一個feature: 帳單(bill)
而這個問題的數學函數結果正是上圖中顯示的綠線，我們可以從綠線看出bill與tip的關係。
更近一步的我們就可以從bill去預測tip會有多少。

而現在這題目因為只考慮一種feature，只有二維的線性關係，線性也表示著連續的結果。
我們可以考慮更多的features，這個結果也會更多維度。

在regression problems中，我們的目標是最小化我們「預測的結果」與「實際的結果(label)」的誤差，
我們常用的計算誤差的方法叫做均方差(mean squared error)

Classification problem

一樣也是昨天的問題，另外一個我們提到的例子，
我們想從其他資訊features預測「顧客的性別」
「顧客的性別」是我們的預測的目標，也就是我們的label
也因為「顧客的性別」是不連續值，所以這是個classification problem。

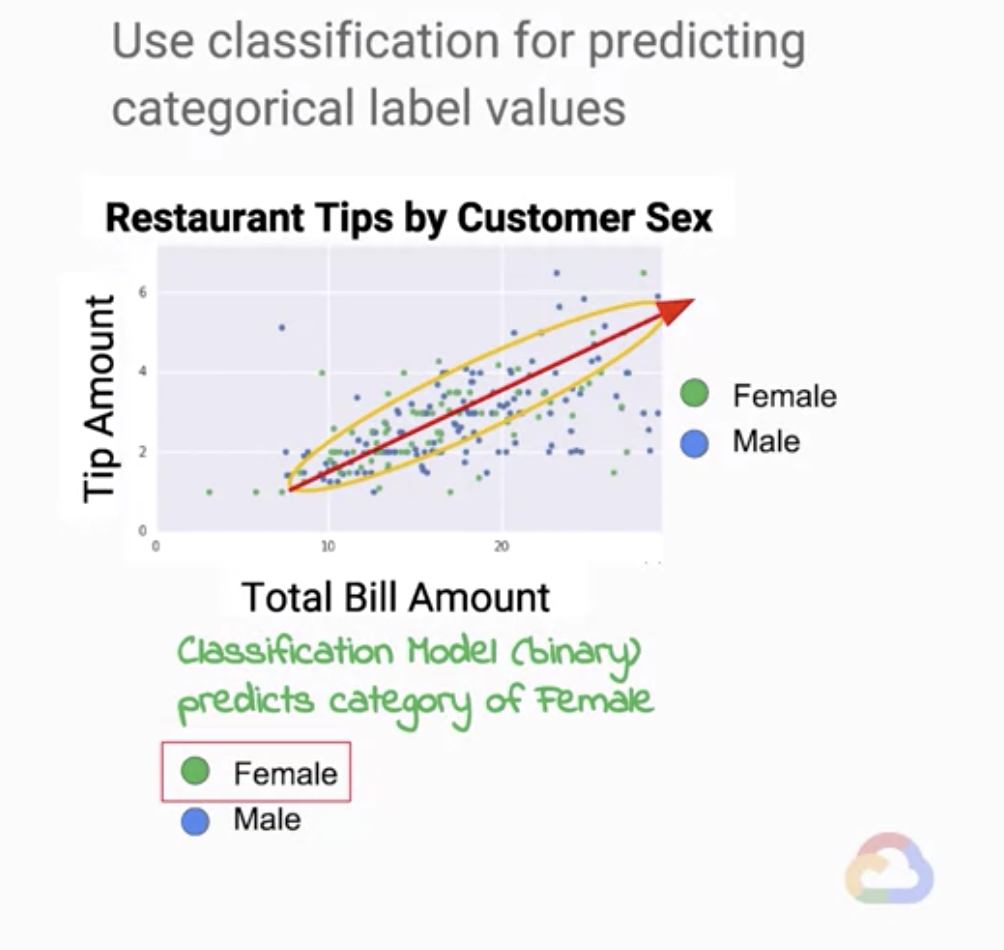
我們看與上面一樣的圖，我們想用tip和bill去試著預測顧客的性別，
但我們會發現這是個不好的idea，我們的仔細看這張圖裡面，
男女的分佈非常的不明顯，所以結果一定也不太好。

這個例子就很好說明了當我們想預測的東西「不是連續」的差別，
性別是一個不連續的資料，當作為我們的預測的目標(label)時，
這就是一個classification problem

在classification problems中，我們使用features預測的結果不會是一個連續的值。
我們用features創造一個抉擇邊界，這個邊界幫助我們區分(分類)出結果label

在這個例子中，一樣我們也會畫出一條線，而這條線的兩側會代表著兩種不同的類別(class)，
例如隨便假設tip比0.18倍的bill值還大(紅線)，我們就預測這位顧客可能是為男性，
(當然在這個例子中我們可以看出這樣的預測結果明顯是錯誤的，我們可以看到有很多反例)

我們知道在這個例子中抉擇邊界(紅線)應該不會是線性的(non-linear)，
在這張圖中我們取黃線部分的結果會是更好的，問題是我們要怎麼要確定黃線比紅線好?

在classification problems，我們的目標是最小化「誤分類(misclassification)」的數量，
也就是我們「預測的分類」與「實際上的分類label」的誤差要為最小。
我們常用的計算誤差的方法叫做交叉熵(cross-entropy)。

另外，就算是預測tip，如果我們不用明確知道tip的值，
我們也可以用classification problem方式解，
假設我們可以將tip分成低中高三個等級：

• 高：高於total bill的25%
• 中：介於total bill的15%~25%之間
• 低：低於total bill的15%

換句話說，我們把價格用區間的方式「離散化」了，
現在「tip等級分類」的問題就是一個classification problem，
一般來說，原來的連續feature都可以被「離散化」成為分類特徵(categorical feature)

當然，反過來將分類特徵(categorical feature)嵌入至連續空間(continuous space)也是做得到的，
這我們會在後面的章節討論，
但不論如何，regression與classification問題皆是「預測問題」，
對比於unsupervised problems的「描述問題」，方向是截然不同的。

參考資料

• coursera - Launching into Machine Learning 課程

• 若圖片有版權問題請告知我，我會將圖撤掉