前言

(我們今天要先進第四章節囉~)
這幾天的文章會是一系列的，會需要一起看才比較能看懂整個ML模型的輪廓，
然而因為一天能寫的內容量有限，所以我會在前言部分稍微說明我寫到哪。

複習一下ML的整個訓練過程

因為ML模型的訓練階段章節內容會分很多部分，我們要先確認好自己在哪個階段，
以免吸收新內容卻不知道用在內容的什麼地方。

★ML的整個「訓練過程」：這裡以監督式學習(Supervised Learning)為例

★小實驗系列：

Course - Launching into Machine Learning

第四章節的課程地圖：(紅字標記為本篇文章中會介紹到的章節)

• Generalization and Sampling
  • Introduction to Generalization and Sampling
    • Introduction
  • Generalization
    • Generalization and ML Models
    • When to Stop Model Training
  • Sampling
    • Creating Repeatable Samples in BigQuery
  • Demo of Splitting Datasets in BigQuery
  • Lab: Creating Repeatable Dataset Splits
    • Lab Introduction
    • Lab: Creating Repeatable Dataset Splits in BigQuery
    • Lab Solution Walkthrough
  • Lab: Exploring and Creating ML Datasets
    • Lab Introduction
    • Lab: Exploring and Creating ML Datasets
    • Lab Solution Walkthrough
  • Module Quiz

0. 一樣先來整理今天重點

★ 名詞解釋：

• 泛化(generalize)：指ML模型「對未知資料集」的預測能力。

泛化(generalize)能力差：等於預測「對未知資料集」的預測能力能力差。但如果對「對自己的資料」的預測能力很好，有可能是發生了過度擬合(overfitting)的現象。

★ 欠擬合(underfitting) 與 過度擬合(overfitting)

自己的註：

「最佳的ML模型訓練結果」應該介於欠擬合(underfitting) 與 過度擬合(overfitting)之間。

★ 用圖簡單解釋 欠擬合(underfitting) 與 過度擬合(overfitting)：

1. Introduction to Generalization and Sampling

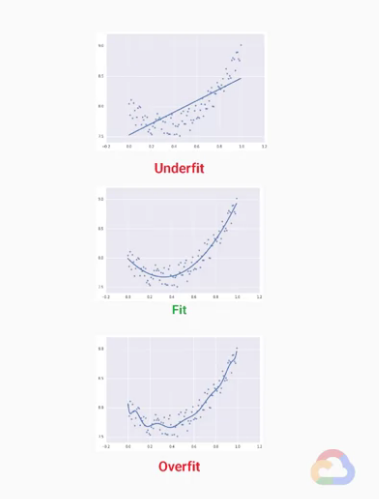
課程地圖

• Generalization and Sampling
  • Introduction to Generalization and Sampling
    • Introduction

我們在這章節要討論的是泛化(generalization) 與 取樣(sampling)

在討論之前，我們一樣來複習前面所學過的內容，
我們已經討論過ML model是如何訓練的，
並且在TensorFlow playground中做了實驗，看到了視覺化的結果。

現在我們就可以思考一個有趣的問題，
什麼時候一個被訓練很精確的ML模型，實際上卻不是正確的結果，

事實上這個問題的關鍵就是在：

「對我們的模型而言的loss為0，實際上在現實生活中並不一定是真的好的。」

自己的註：

對一個資料集的分析，loss為0僅代表「這個誤差對資料集的預測沒有影響」，不等於預測是對的。

★ 「好的ML模型」不是指對「我們的資料集」預測結果好，而是對於「未看過的資料」表現的也好。

我們的ML模型如果將來想要產品化，這表示會有更多我們的ML模型沒看過的資料，
這就是我們必須仔細評估的問題。

所以我們要來討論怎麼去「評估我們沒看過的資料」?

首先，我們必須要得到一些我們沒有在訓練中使用的資料，
在我們的訓練完成後，我們就可以用這些資料來評估，

我們也可以藉由這樣的評估來判斷我們的模型是否有過度擬合(overfitting)的現象，
以及確定什麼時候應該模型要停止訓練。

第二部分就是我們可以如何在一開始就創造一些未知的資料集，
正常情況下，我們可能很難取得未看過的資料。

但因為我們有訓練資料集，
所以我們可以將訓練資料集拆成「訓練用」與「評估用」，
我們可以使用其中一組資料集訓練我們的模型，
而當模型訓練完成時，我們就可以使用另外的資料來進行測試與評估模型的表現。

所以我們也會學到如何去建 training, evaluation, test 的資料集，
並透過這樣的方式實際建立測試模型的指標。

2. Generalization and ML Models

課程地圖

• Generalization and Sampling
  • Generalization
    • Generalization and ML Models

我們先來解決泛化(generalization)的問題，這可以幫助我們理解
「為什麼我們訓練一個預測準確的模型，並不一定是最好的模型。」

2.1. 觀察過度擬合(overfitting)的現象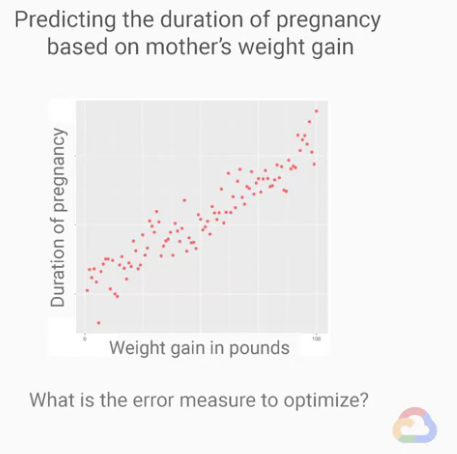

我們再來看一下我們所熟悉的出生率資料集，
不過這次我們使用「母親的體重增加」在X軸上，
來預測在Y軸上的「預測懷孕的時間」，

首先我們可以直覺的感覺到，這兩組資料看起來有很強的相關性，
也就是說，體重增加的越多，懷孕的時間就越長，
這件事情似乎在嬰兒的成長過程中是很直觀的。

我們也來複習前面一點的內容，當我們說到要對這樣的關係建立模型，
證明這兩個數據具有相關性，我們需要使用線性回歸模型(linear regression model)
而當我們討論回歸問題(regression problems)時，
我們通常用來計算的loss的方式都是MSE(mean squared error)或RMSE(root mean squared error)

• MSE

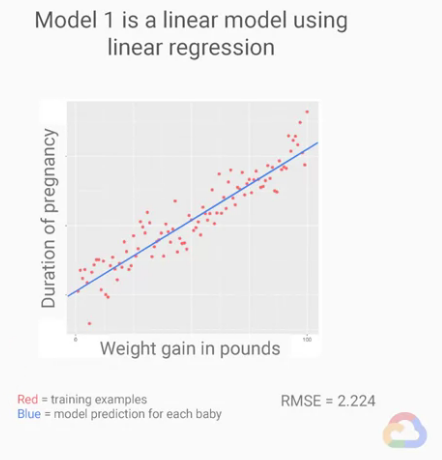
MSE(mean squared error)可以告訴我們我們預測的回歸線與實際結果有多接近，
我們實際上在計算就是「每個資料點」與「回歸線(我們的預測)」的距離，
這段距離我們又可以稱為error(誤差)，
在MSE(mean squared error)的計算之下，我們會將誤差平方，
所以我們會移除負號而只觀測其值。
此外，因為MSE的關係，我們可以加重「預測」與「實際值」差異的處罰。

• RMSE

用MSE取平方根即可得到RMSE，RMSE有點像所有數據與預測的平均距離。
而因為RMSE能夠修正單位的問題，我們能直接解釋為Y軸上的測量單位。
所以以相關係數來說，RMSE會是個更好的測量單位。

不論是這兩種誤差的測量，越小的值都表示模型的性能更好，
我們期望這樣的模型訓練最後能越接近零(表示預測沒有誤差)

這裡我們使用線性回歸模型(linear regression model)，
我們透過這模型簡單的繪製了一條最佳回歸線，最大程度的減少了誤差，
我們最終的RMSE值為2.224，似乎還不夠小，那我們來看看另外一個例子。

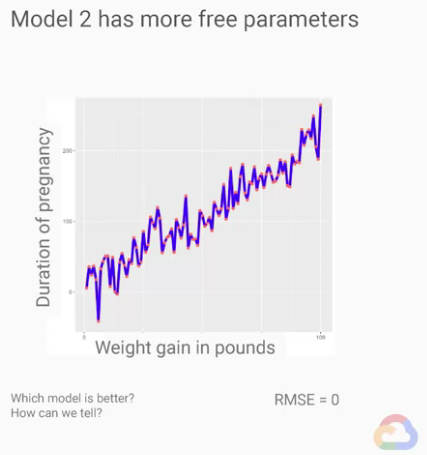
我們現在來看上面這個有趣的圖形，
我們現在使用更複雜的模型來預測，更複雜的模型會有更多的參數(parameters)

在這個例子中，這些參數(parameters)替我們捕獲到了資料集的每個資料的細節，
然後我們的RMSE值就降到0了，現在這結果「對於我們的資料集」非常的精確。

然而這樣的結果真的是最好的嗎? 我們能使用這模型來生產嗎?

其實這結果非常的有問題，我們舉個例子，
如果今天來了一個我們沒看過的資料，我們訓練出的模型就沒有這樣的直覺，

所以如果問我們，具有8個node的比12個node的好嗎?
我們有個16個node的神經網路，他有最低的RMSE，我們應該使用這個嗎?
我們在這裡所看到的例子，可能是有數百次方的多項式，然後具有數百個node的神經網路。

雖然更多的node(也代表更複雜的模型)能夠幫助我們優化更多的參數，
也能幫助我們找到最適合「複雜數據的分類」結果，
(例如像上一張分類螺旋資料集的例子)
但同時，這樣子做也會讓模型去記住更簡單的、更小的數據集。

自己的註：

就是把整個數據集都「背下來」了，但「不是這個數據集」的反而不會了。
這就是過度擬合(overfitting)。

2.2. 泛化(Generalization)

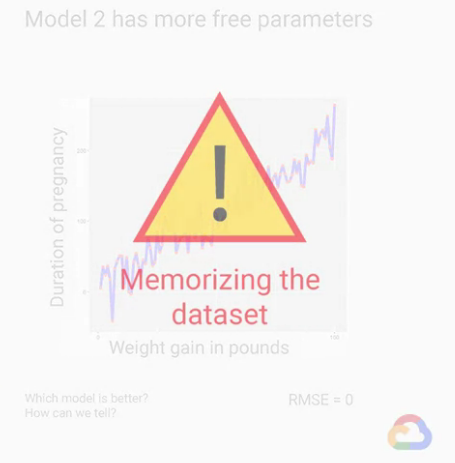
所以，我們應該要在什麼時候停止訓練模型?
並且我們要避免模型「背下資料集」導致過度擬合(overfitting)?

現在我們有個驗證模型的方法，就是拿我們的模型給沒看過的新資料集看性能如何，
然後我們就可以決定現在的模型對新資料集的泛化(generalize)程度如何，
這也會是未來我們在生產ML模型的重要指標。

自己的註：

泛化(generalize)：基本上就是指ML模型對未知資料集的預測能力。
如果沒有良好的泛化(generalize)，表示我們的模型只對我們的資料集預測好而已。

我們現在再回到線性回歸模型(linear regression model)與神經網路模型(neural network model)，然後看它們表現的怎麼樣。

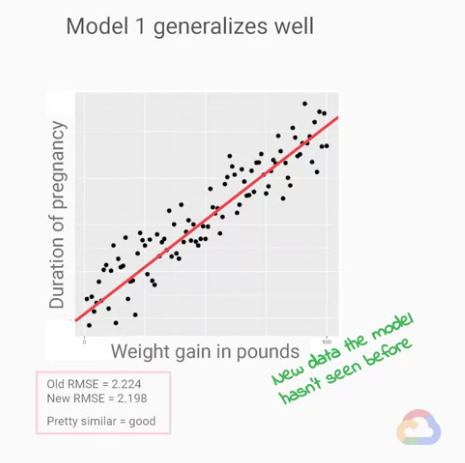
我們的線性回歸模型(linear regression model)對於新資料集的「泛化(generalize)能力非常好」

從我們「新資料集計算出」的RMSE與我們「訓練所計算出」的RMSE差不多可以判斷。
在這樣的情況下，對於我們的ML模型是一件好事。
我們就是希望再預測(training)與驗證(validation)過程中，
我們的模型能有差不多的表現。

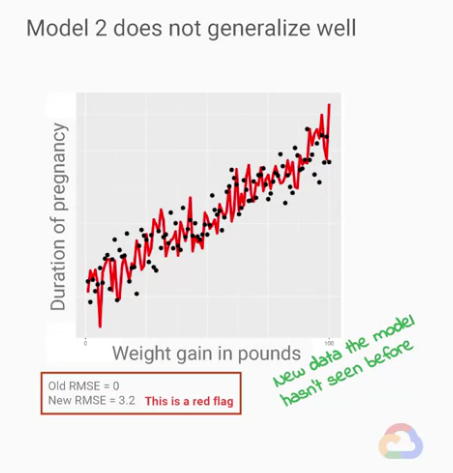
我們現在看到第二個模型，我們可以發現他對於新資料集的「泛化(generalize)能力非常差」

就算對於我們「訓練所計算出」的RMSE為0，
對於「新資料集計算出」的RMSE從0跑到3.2，
這代表一個非常嚴重的問題，也指示出我們的模型有著過度擬合(overfitting)的現象，
也證明了這模型對於新資料的預測能力非常的弱。

2.3. 泛化(Generalization)問題的解法

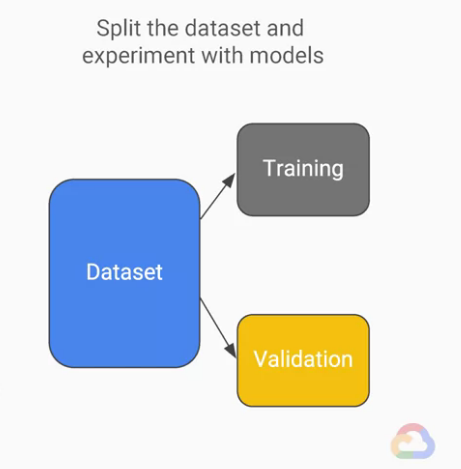
現在我們可能會想問，怎麼確定我們的模型訓練有沒有過度擬合(overfitting)?
所以我們該如何決定我們訓練停止的時間? 這個問題的答案十分的簡單。

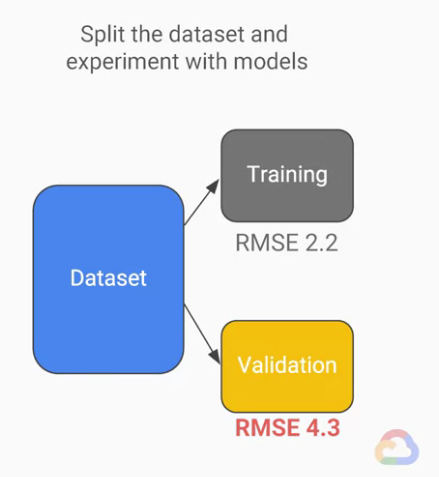
我們先將我們的資料集分成兩部分。
現在我們將我們的原始資料分成完全兩個獨立的組別，
一個為「訓練用資料集(training)」、另一個為「驗證用資料集(validation)」

我們可以拿我們的「訓練用資料集」來不斷的反覆訓練我們的模型，
當我們完成訓練之後，拿訓練好的模型使用「驗證用資料集」來看模型的表現。

如果模型泛化(generalize)的很好，它應該也會在「驗證用資料集」有差不多的loss值
(也就是「訓練用資料集(training)」、「驗證用資料集(validation)」的loss差不多。)

當我們看見我們的模型對於「驗證資料集(validation)」預測結果開始不好的時候，
也就是像上圖，當我們計算出的loss開始增加，我們的模型訓練就該停止了。

自己的註：

正常來說「驗證資料集(validation)」的RMSE應該也要差不多2.2左右
誤差太大也表示我們的ML模型有可能在「背資料」了。

同時訓練和驗證ML模型，能夠幫我們找到正確的泛化結果與最合適訓練資料集的模型參數，而不是將模型整個背下來。

2.4. 欠擬合(underfitting) 與 過度擬合(overfitting)

欠擬合(underfitting)

我們先看上圖中最上面的圖形，
我們有一個過於簡單的線性模型，它並不太適合預測我們這組資料，
上圖中，我們可以視覺上的發現很多點都是在這條預測之外，
這樣的情形我們就稱為欠擬合(underfitting)

過度擬合(overfitting)

而與上述相反的情況，如果結果太過符合所有的資料點，
我們就稱之為過度擬合(overfitting)

我們適當增加線性模型(linear model)的複雜度，使它成為n階多項式，
讓結果能符合我們資料的預測，

因此，這就是為什麼我們需要驗證的資料集，
我們就是要決定是否模型的參數是否已經過度訓練導致過度擬合(overfitting)的發生。

過度擬合(overfitting)或模型「只知道」我們訓練資料集的如何預測，
很多時候都會到生產階段才知道，這也就是為什麼我們還需要驗證的資料集。

一個正確的結果，也就是在欠擬合(underfitting)與過度擬合(overfitting)之間找到適當的模型複雜度，

接下來我們就要來看如何使用驗證資料集(validation dataset)，幫助我們決定模型停止訓練的時間，與他是如何幫助我們避免過度擬合(overfitting)。

參考資料

• coursera - Launching into Machine Learning 課程

• 若圖片有版權問題請告知我，我會將圖撤掉