現在讓我們簡要介紹一下機器學習的歷史，看看它是如何隨著時間的推移演變成今天如此受歡迎的深度學習神經網路。[來自課程內容]

機器學習的方法有很多，但是並非一開始就是使用神經網路，事實上在走道神經網路這步之前，我們為了預測所建立的數學模型多到數不完，而最初，線性回歸是一個關鍵！

線性回歸被發明用於預測行星的運動，以及預測豌豆莢的大小。
弗朗西斯·高爾頓爵士率先使用統計方法測量自然現象。他正在研究父母和孩子在包括甜豌豆在內的各種物種中的相對大小的數據。他觀察到一些不是很明顯的東西，一些非常奇怪的東西。
一個大於平均水平的父母往往會產生比平均水平更大的孩子，但這一代孩子的平均水平要高出多少？
事實證明，這個孩子的比例低於父母的相應比率。例如，如果父母的大小在其自己的一代中與平均值相差1.5個標準差，
那麼他將預測孩子的大小將小於其隊列中平均值的1.5標準偏差。我們說一代又一代，自然界中的事物倒退，
或者回到平均值，因此得名，線性回歸。這張圖來自1877年，是有史以來第一次線性回歸。[來自課程內容]

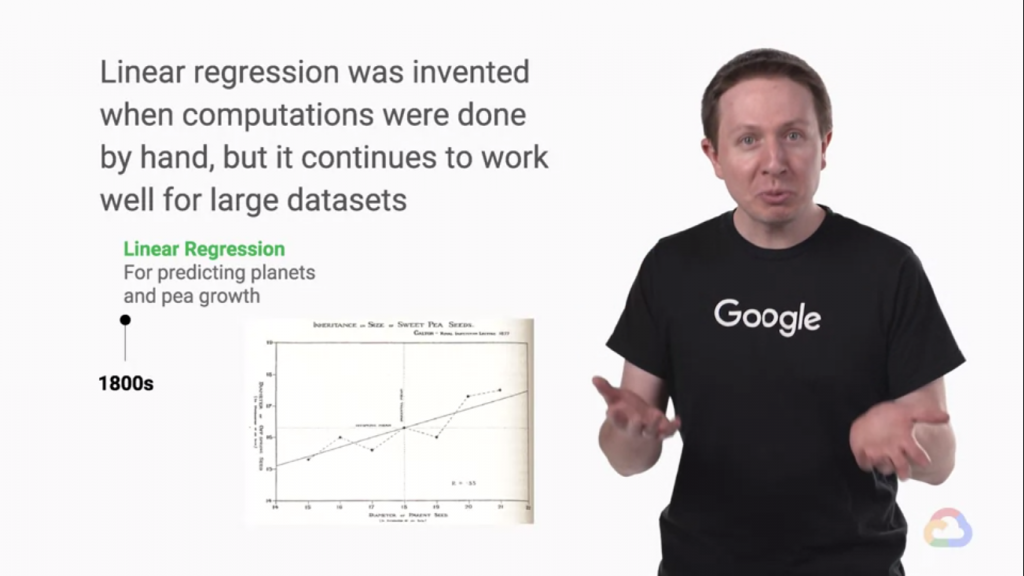
世界上第一個回歸預測就這麼誕生了！

19世紀的計算能力有限，因此一旦我們擁有大型數據集，他們甚至都沒有意識到這種情況會如何繼續發揮作用。[來自課程內容]

再來我們要把鏡頭轉到線性回歸的核心了！

我們從線性方程開始，我們假設通過將各種權重與我們觀察到的特徵向量相乘，然後將它們全部加起來來描述我們的系統。
對於我們數據集中的每個示例，我們可以在上面的等式中表示這一點，y = w0乘以x0 + w1乘以x1加w2乘以x2，依此類推我們模型中的每個特徵。
換句話說，我們將此公式應用於數據集中的每一行，其中權重值是固定的，並且特徵值來自每個關聯列，以及我們的機器學習數據集。
這可以很好地打包到下面的度量方程中，y等於X乘以w。[來自課程內容]

各位又一頭霧水了對吧，我們在做線性回歸時通常輸入只會有一個(X)，而我們要透過X來預測(Y)，這時我們在求用來預測的線(X&Y的關係)就是線性回歸了！但是在機器學習領域我們不可能永遠只有一個輸入(X)，我們將會有多個輸入，
而這些輸入將會根據他們影響結果的大小來乘上權重！於是我們可以把X與Y的數學關係式寫成上面這副德性！
在簡化一點就會變成上圖下面的式子！

這個關係是不僅可以解釋線性回歸，更可以解釋在Machine Learning領域神經網路的運作方式！
而我們在做Nearul Network最重要的就是權重的更新，把權重更改到最Fit資料的Model(同時不能Over fitting)
不過我們該如何讓ML model知道它離症瘸答案還有多遠呢？答案就是MSE，答案就是均方誤差，
均方誤差是拿來表示誤差的好方法，我們用我們的Label(正確答案)來扣掉ML model的預測，我們可以稱之為"誤差"
那麼我們為甚麼要用均方誤差來告訴ML model它錯了多少呢？
首先，我們訓練的資料一定都是龐大的資料，我們不可能每傳播一筆資料後就更新一次權重！而每次的誤差有正有負
，當這些誤差的正負號沒有消除時，我們會得到很大的問題正的誤差會悍婦的誤差相抵，而形成了明明是很大的誤差
但是相抵後卻變的非常小！這時消除正負號就變成了很重要的工作，"平方"就是一個好方法！
利用均方誤差可以在誤差大時加速Model的收斂速度！(這個後面的文章有緣再說吧~)我們要回到課程。

我們透過 LossFunction (來計算模型誤差的Function，上面有提到通常使用MSE)就可以知道一個 ML model的學習狀況，而ML model在學習時，
梯度就是一個很重要的概念，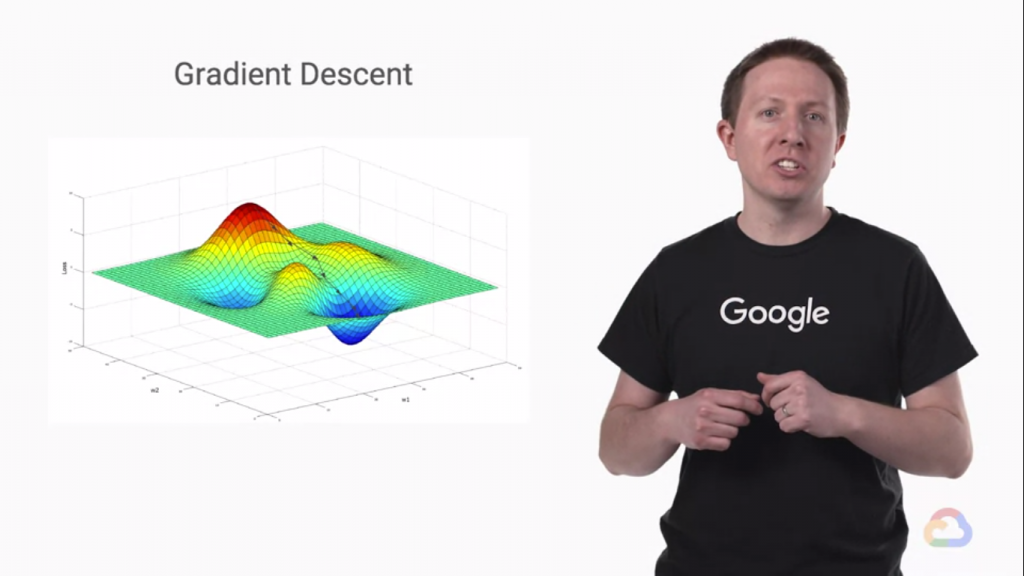
這是Loss Function的假想圖，Loss Function的維度通常會更高，但是更高維度的圖我們畫不出來了！
於是我們用三維的圖來看，可以看到在Loss Function中有山峰也有山谷，在這種三維向量中我們稱改變X可以讓Y往最高點走的方法叫做"梯度上升"，而在Loss Function 中因為它代表的是誤差，所以我們必須要讓梯度降到最低點，
既然"梯度上升"是往最高點走的捷徑，梯度上升是讓函數內所有參數加上"梯度"，所以我們要最快的下降的話，
當然是扣掉"梯度"了！而扣掉梯度這個方法就叫做"梯度下降" Gradient Decent。而Gradient Decent也是Neural
Network反向傳播(學習時)的核心演算法。

-今天打得比較快，如果有錯字麻煩告知QAQ