上一篇我們可以看到，可以利用ML技術來預測的兩個問題，回歸(Regression)與分類(Classification)，
而這裡種問題相信搭家應該都可以輕易地分辨了，今天我們就要來深入的瞭解這兩大問題！

1.回歸(Regression)與分類(Classification)

在上一篇舉的例子，預測服務員的小費，我們可以邱處的了解到回歸(Regression)與分類(Classification)問題的差別，在上述的例子中，服務員的小費是連續性的數值，這告訴我們它是一個回歸問題！
在回歸問題中，目標是使用不同特徵組合的數學函數來預測我們標籤的連續值。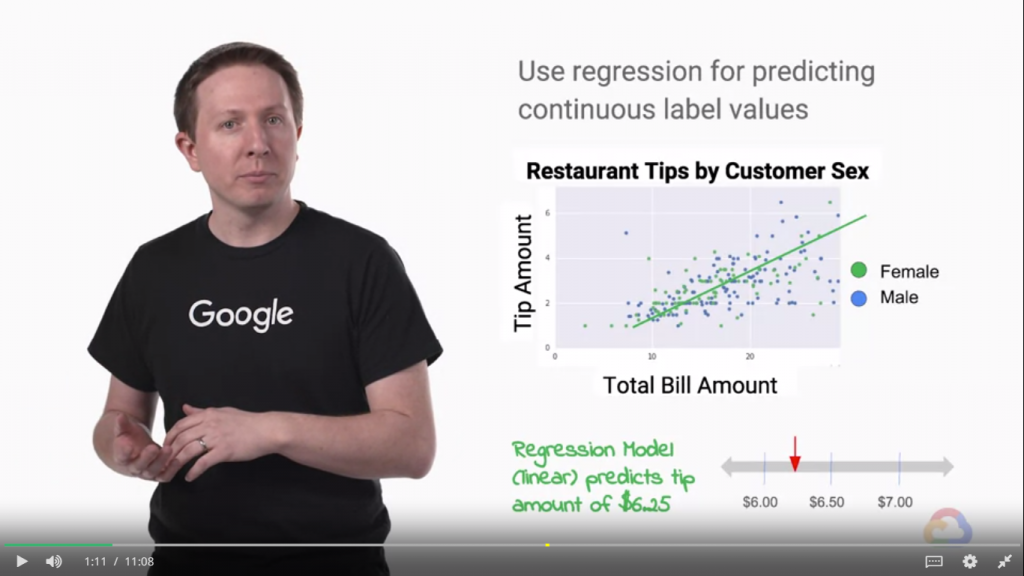

看到圖片，其中對於總賬單金額乘以線的斜率，可以得到小費的連續值。平均小費是總賬單的18％，那麼線的斜率將是零點一八！

通過將賬單金額乘以0.18，我們將可以獲得預測的小費。只有一個特徵的線性進展可以推廣到其他特徵。
這種情況下，我們如果有一個多維問題，概念是相同的。每個示例的每個特徵的值乘以超平面的梯度，這只是一條線的推廣，以獲得標籤的連續值。[來自課程內容]

上面的例子就是在講回歸！如果看不懂，我們可以簡單的理解成，圖中那條直線就是我們從旁邊的點，做回歸而求得的！
而我們透過大量資料做回歸後，取得這條直線，就可以利用這條直線做預測！而現實中的資料不會這麼剛好都是二維的，
可能會出現多為的資料，而圖無法表達這種多維度的資料，但是我們同時也可以利用這種類似單維度回歸的方式，來找到
最佳擬合的直線、平面或多維的直線甚至是超平面。

而如果這時我們把性別的問題考慮進來！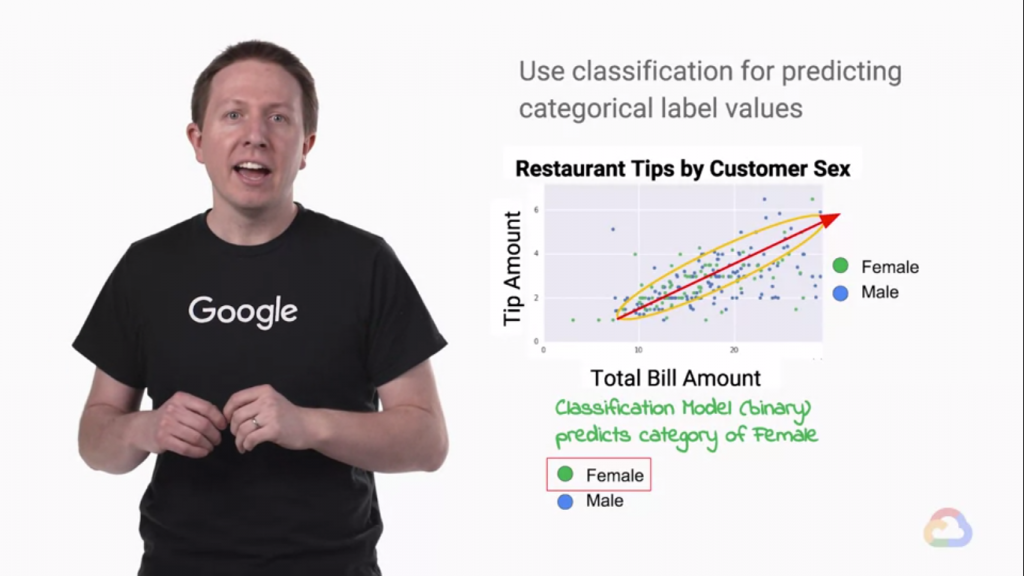

但是，嘗試這樣做有助於我說明當你想要預測的東西是絕對的而不是連續的時會發生什麼。
至少在該數據集中，性別列的值是離散的，男性或女性。因為性是絕對的，
我們使用數據集的性別列作為我們的標籤，問題是分類問題。在分類問題中，
我們試圖創建一個分隔不同類的決策邊界，而不是試圖預測連續變量。所以在這種情況下，
有兩類性別，女性和男性。線性決策邊界將形成更高維度的線或超平面，每一類都在兩側。
例如，我們可能會說，如果提示金額大於總賬單金額的零點八倍，那麼我們預測付款人是男性。
這由紅線顯示。但這對於這個數據集來說效果不佳。男性似乎有更高的變異性，[來自課程內容]

當我們把焦點放在兩個性別時，性別的數據又對這次回歸(Regression)的例子可以造成多少影響？
上圖可以看到這兩個性別在上圖中，混雜的程度高的驚人，根本是混在一起的。這代表我們不能透過性別預測嗎？
才怪！

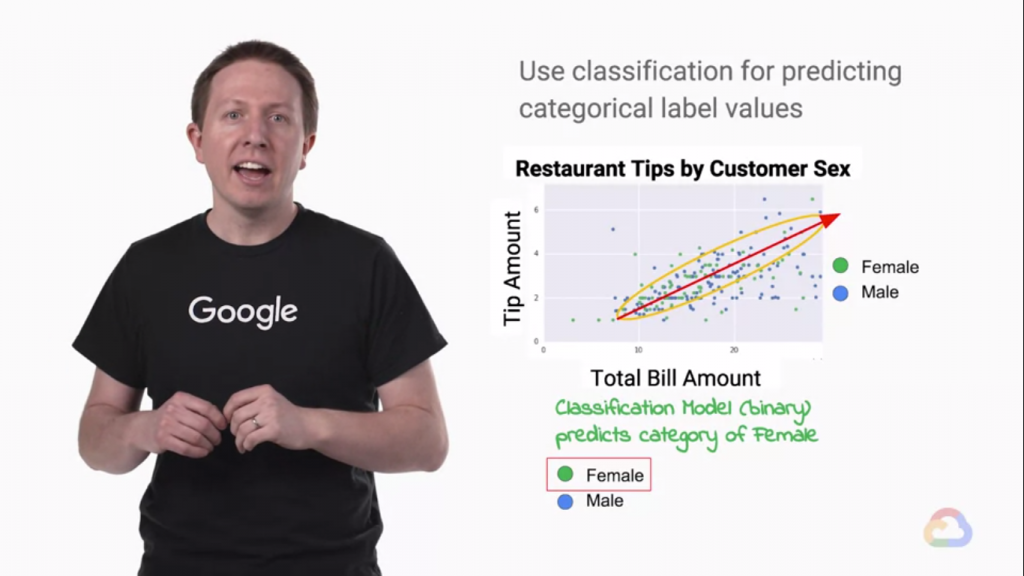
女性則傾向於在更窄的範圍內傾斜。這是一個非線性決策邊界的例子，由圖中的黃色圈表示。
我們如何知道正確的決策邊界是壞的，黃色決策邊界更好？在分類問題中，
我們希望最小化我們的預測類和標籤類之間的錯誤或錯誤分類。這通常使用交叉熵來完成。
即使我們預測提示量，也許我們不需要知道確切的提示量。
相反，我們想確定提示是高，平均還是低。我們可以將高尖端量定義為大於25％，
平均尖端量為15％至25％，並且尖端量低於15％。換句話說，我們可以離散金額。

女性在這個例子裡比較傾向靠近回歸線(黃圈部分)，這是ML model可以在大量數據中找到的線索！
所以把性別資訊輸入給ML model Train 也是能達到一點效果的！

最後我們來看看一個問題。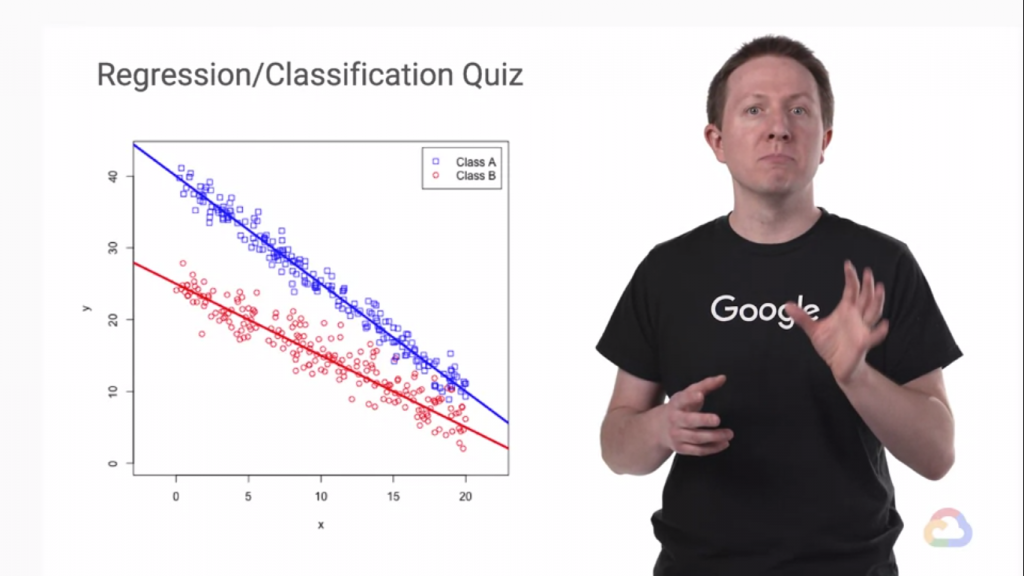

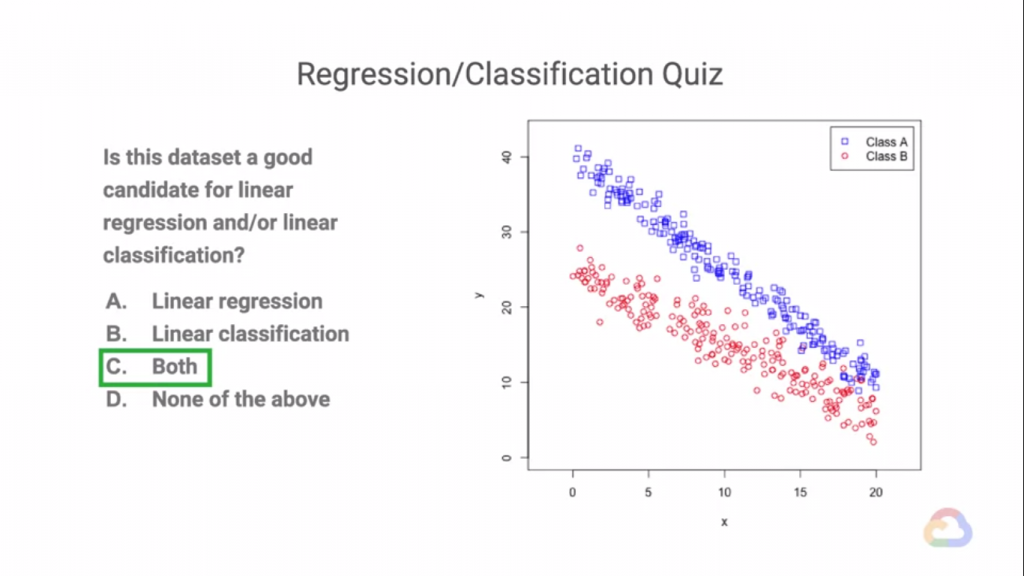
這張圖應該是回歸(Regression)還是分類(Classification)的問題呢？

答案是：都是！

可以看到我們在這份資料的兩個類別分別求出回歸直線，這拿來做回歸(Regression)的情況，但是我們就不能做分類的嗎(Classification)？我們當然可以在中間切出一條直線把這兩組分開！就變成分類問題了！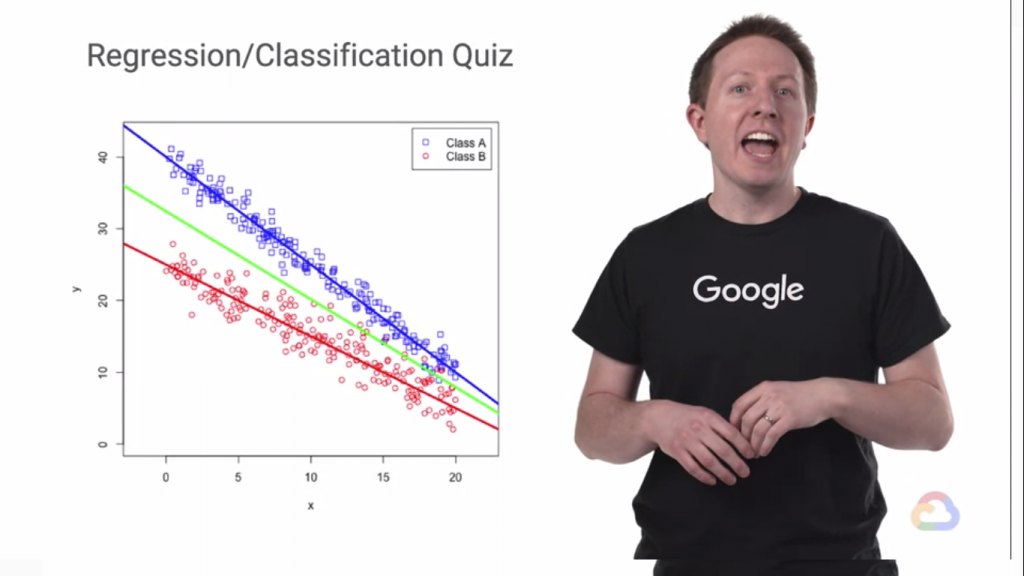

而可以看到這條綠線切得不是很好(上面來有一些藍紅點交雜在一起！)，真的是這樣嗎？
在更高的維度看下去，並不是這樣的！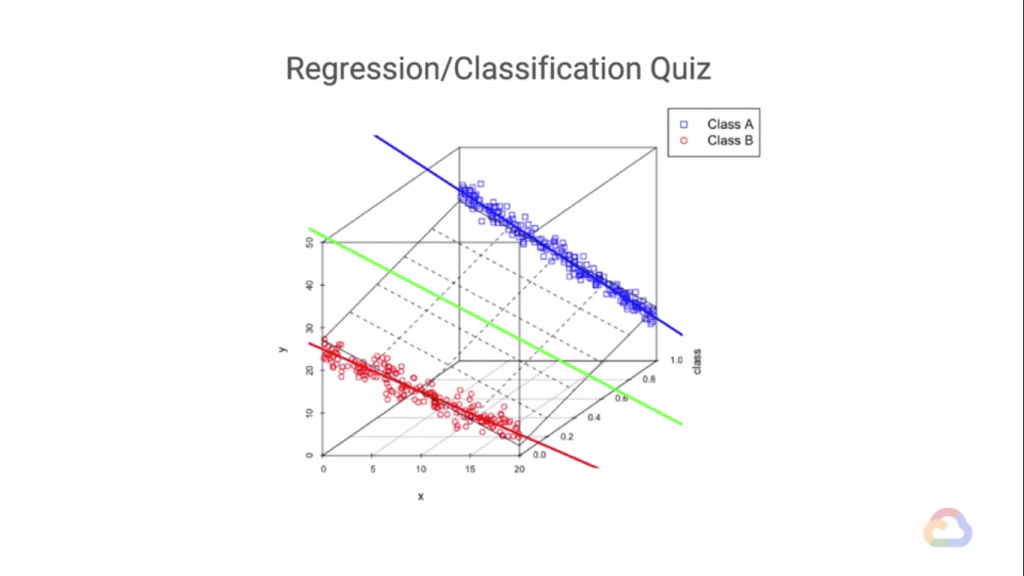

更高的維度下，資料被完美的分開了，而這只是三維的維度而已，在更大的維度上我們畫不出來！
但是同理，我們可以找到最佳的擬合直線、平面、甚至是超平面...等。

今天是第18天，明天禮拜一！工作愉快~