黑色好看版 - 傳送門

正文開始

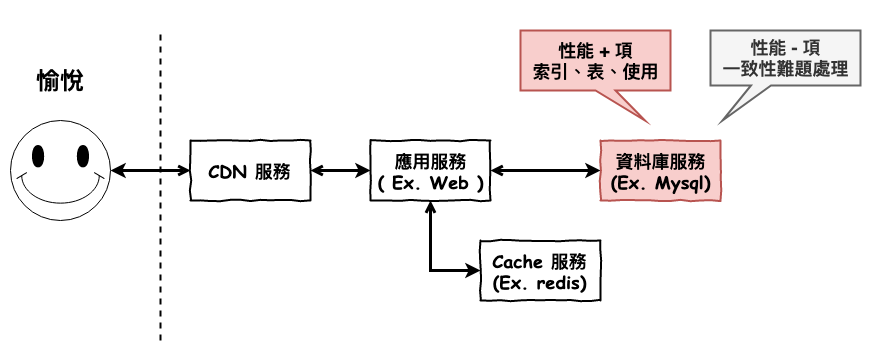
接下來咱們要來理解資料庫系統中最核心的問題 :

要如何儲放資料，才能更快速的找到資料呢 ?

而這個東西的技術就是所謂的 :

索引

而在 mysql 中決定如何儲放的是資料庫儲存引擎來決定，而這裡咱們將要從 mysql 預設引擎 innodb 來深入的理解一下。

在 InnoDB 中預設是使用『 B+樹 』來當資料儲放格式，而為什麼要選擇它呢 ?

這就是我們這篇文章的重點。

InnoDB 為什麼選擇 B+ 樹 ?

本篇文章分為以下幾個章節，這也就是 B+ 樹的誕生原由。

• 二分搜尋 Binary Search
• 二元搜尋樹 Binary Search Tree
• 平衡二元搜尋樹 Balanced Binary Search Tree
• B 樹
• B+樹 ( InnoDB 的選擇 )

二分搜尋 Binary Search

首先我們都知道，資料庫誕生出來的本質就是為了讓我們找東西更快速。

那是和什麼比呢 ? 就是所謂的『 線性搜尋 』，也就是說有 1000 筆資料，你要找到你想要的值，需要一筆一筆的慢慢查，而這種線性搜尋的時間複雜就是 O(n)，其中 n 就是你所有的資料量。如下圖 1 所示。

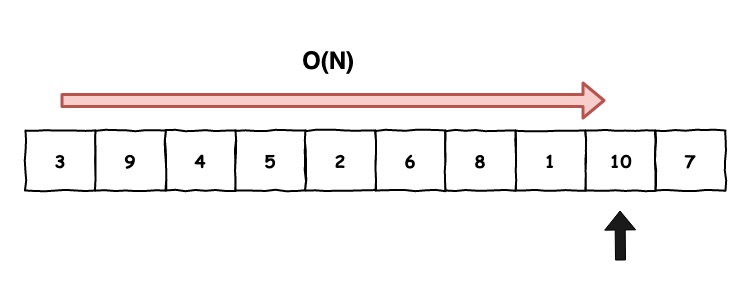
圖 1 : 線性搜尋

那要如何加快呢 ? 基本上就是將它整理成固定的規律與特性，讓我們可以根據這個規律進行一些更快速的搜尋，這就是所謂的資料結構。

而最初在設計時，所選擇的規律概念就是所謂的『 二分搜尋 』。

要使用二分搜尋的前提條件為 :

• 必須是排序好的資料

它的思路為 :

將資料砍成兩半，每一次砍時，判斷你要的資料在左還右 ( 因為是排序，所以可判斷 )，然後再從那段重複一樣的事情。

範例圖如下 :

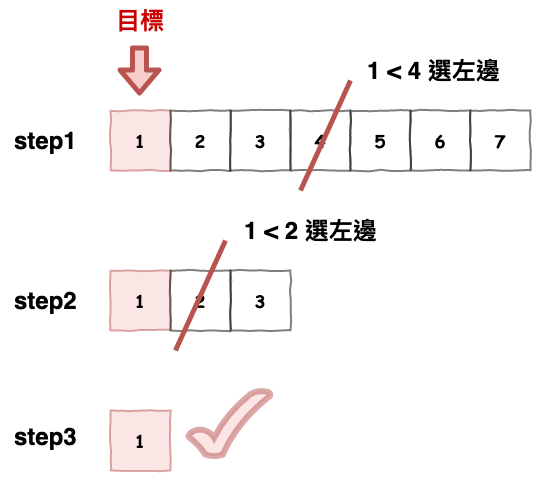
圖 2 : 二分搜尋概念

那要選那個資料結構來實現二元搜尋呢 ?

資料結構只是一種概念，比較關鍵的重點在於記憶體的連續性，而這個連續性就可以導出兩個資料結構，那就是『 array 』與『 list 』。

Array ( X )

不行。主要有以下兩個原因。

• 它的記憶體是連續區塊，需先事先分配大小，大量資料新增、刪除時會很浪費資源。
• 新增、刪除操作有時會執行很快，有時會很慢，資料庫應該儘可能的操作都是平均。

為什麼 array 在新增或刪除時可能會很慢或很快呢 ?

主要的原因在於，它的記憶體區塊是連續的，所以假設一開始分 5 個位置，然後你新增資料 5 次，這 5 次都是會很快，但是問題出在第 6 次，因為沒有空間了，所以它會進行以下的流程來將 array 變大。

1. 建立原本陣列兩倍大的記憶體空間。
2. 將原本的陣列資料拷貝過去。
3. 在寫入第 6 次資料。

所以基於以上原因，不會選擇這種資料結構。

List ( X )

list 呢 ? 它的記憶體是分散的。不行，因為以下原因如下圖 3 所示，它無法進行二元搜尋，因為它的記憶體是分散的，也就是說如果要至 5，那你要先知道 3 的記憶體位置，它那裡才有記錄 5 在那個位置上。

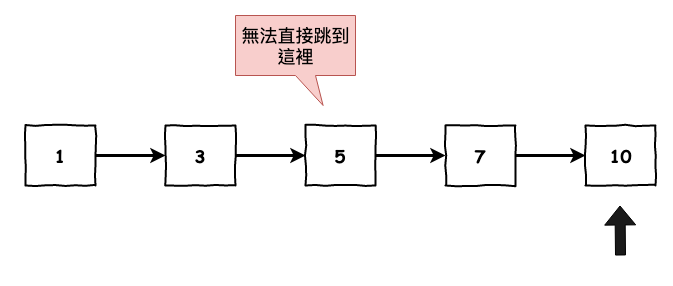
圖 3 : list 進行二元搜尋問題

二元搜尋樹 ( BST Binary Search Tree )

上述說明的兩個資料結構事實上都有某些優點 :

• Array 可以使用 Binary Search。
• List 可以解決 Array 的新增效率問題。

那有沒有什麼資料結構是有這兩個優點呢 ?

那就是『 二元搜尋樹 』，簡稱 BST。

BST 基本上長的如下圖 4 所示，基本特性就是左子樹值一定小於根節點，而右子樹值一定都大於根節點。

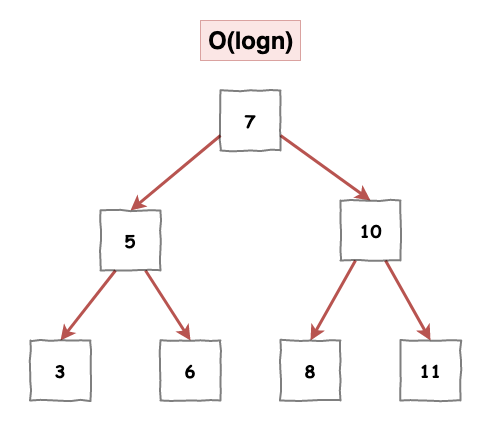
圖 4 : 二元搜尋樹

然後資料庫的操作基本上為新增、刪除、搜尋。接下來我們來說說它們每一個操作的時間。

• 搜尋 : 平均時間複雜度 log(n)，因為只要往其中一邊走。
• 新增 : 平均時間複雜度 log(n)，因為它要找到適當的插入位置
• 刪除 : 平均時間複雜度 log(n)，因為它要找到適當的移除位置

基本上資料庫這三個基本操作平均而言都有 log(n) 指數級的操作時間，正常來說應該是可以選擇它。

平衡二元搜尋樹 ( Balanced BST )

BST 平均來看基本操作都有指數級的時間複雜度，但為什麼還是沒選他呢 ?

主要的原因在於，它最壞變成 O(n) 的時間複雜度操作，如下圖 5 所示，它的確也是一個 BST，這樣如果我們要搜尋某個值，仍然是一個一個慢慢找。

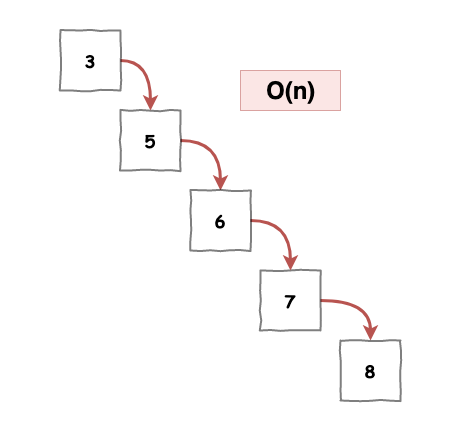
圖 5 : 有問題的 BST

因為後來就誕生一種『 平衡二元搜尋樹 』，如下圖 6 所示，事實和上面二元樹相同，只是差在每當插入節點時，會進行平衡。

它的特點如下 :

• 葉節點的高度差的絕對值不能超過 1。
• 左右子樹都為平衡二元搜尋樹。
• 它的最好、最壞、平均的新增、刪除、搜尋的時間複雜度都是 O (logn)。
• AVL 樹、紅黑樹都是屬於平衡二元搜尋樹，它們都會自動的進行平衡操作。

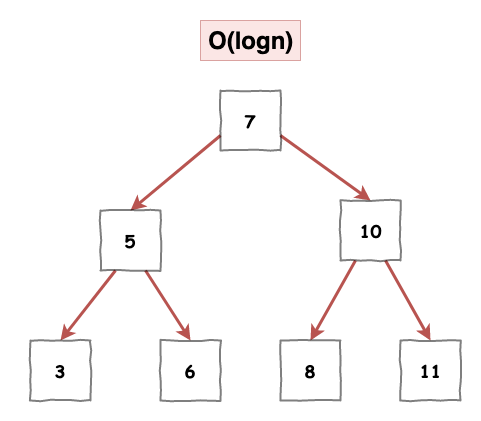
圖 6 : 平衡二元樹

平衡二元搜尋樹，正常來說，已經是在搜尋中最有效率的資料結構了，但是為什麼它是沒選它呢 ?

因為它是以『 記憶體 』來說，操作最有效率，但是以『 硬碟 』來說則否。

在資料庫的世界，通常資料量都有點兒大，不太可能全部都塞在記憶體中操作，通常會放在硬碟中。

那為什麼平衡二元搜尋樹在硬碟中操作沒有什麼效率呢 ?

因為 I/O 的問題

然後你想想如果一個很深的平衡二元搜尋樹，那如果要找的值是在最小面，以下圖 7 為例，那它就至少要進行 100 次 i/o 操作。

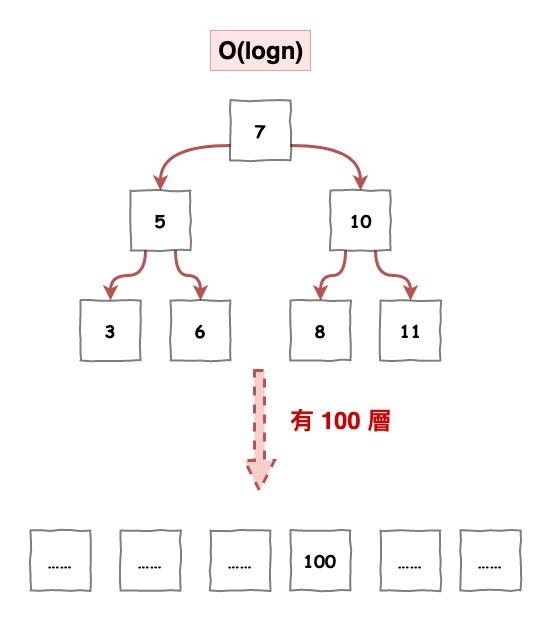
圖 7 : 平衡二元樹在節點多時的問題

B 樹

根據上述 i/o 的原因，因此又誕生出叫『 B 樹 』的東東，它想解決的東西為 :

解決高度太高的所產生的問題 ( ex. 資料庫索引的 i/o 問題 )。

一顆 m 階的 b 樹基本上有以下特點 :

• 每個節點內最多有 m - 1 個內部節點。
• 每個節點最多有 m 個子樹。
• 每個內部節點都有儲放完整資料。
• 每個節點內的內部節點，都是依順序排序。

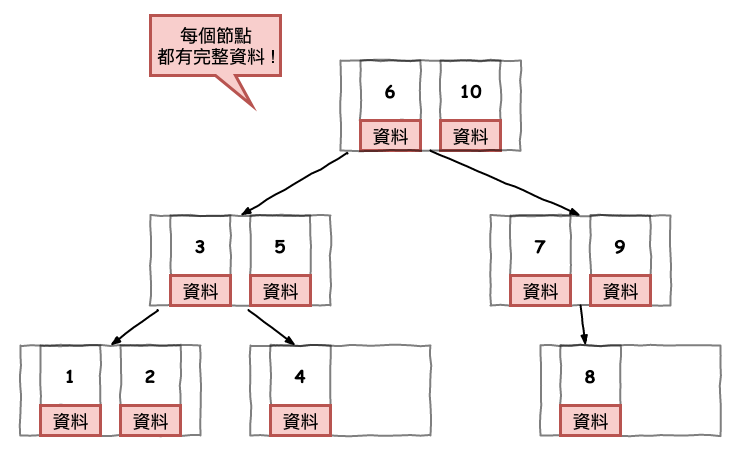
圖 8 : b 樹

基本上它的概念就是在一個節點內，多塞些東西，為了減少 i/o 讀取次數，如上圖 8 所示。

為什麼可以減少 I/O 次數呢 ? 節點不是還是一樣多 ?

主要原因在於，平衡二元搜尋樹，每一個節點都是儲放在一個硬碟區塊中，而這個區塊大小為 4 kb，在讀取資料時都是以一個區塊為最小單位，也可以想成說，不管你節點資料是 2 byte 還是 1 kb，讀取次數都是和 4 kb 的一樣。

所以 b 樹處理的想法，就是儘可能將每個節點都塞滿 4 KB 的資料，並且內部在使用節點來區分，這樣每一次 i/o 讀取就可以讀到多個節點，這樣就可以減少 i/o 次數了。

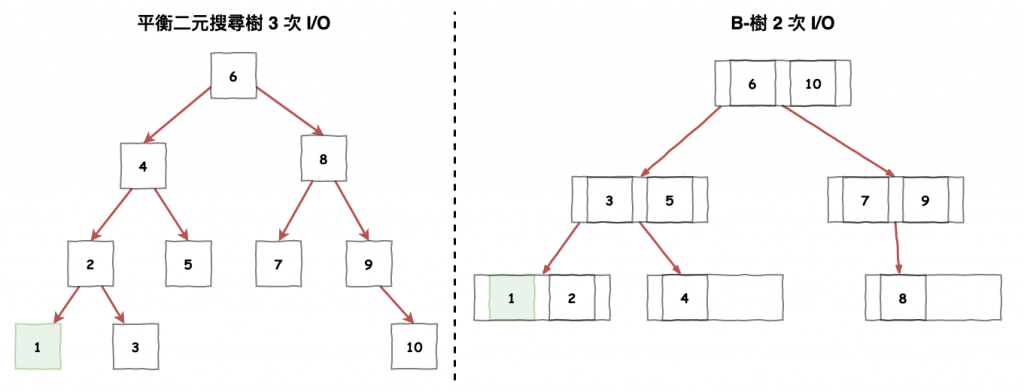
圖 9 : b 樹與平衡樹的 i/o 比較

B 樹的問題

有了 B 樹後，為什麼還需要 InnoDB 仍然沒有選擇它呢 ?

因為有以下幾個問題 :

• 查詢時不穩定。
• 範圍搜尋時沒什麼效率。
• 節點太多會導致 i/o 問題。

查詢時不穩定

假設我們有一個以 b 樹的來儲放的資料，接下來我們要進行兩次搜尋，然後結果如下圖 10 所示 :

• 尋找 10 : 只要 1 次 i/o 就可以找到資料。
• 尋找 1 : 要 3 次 i/o 才可以找到資料。

這就是 b 樹不穩定的範例，最好的情況是根節點就可以找到，而最壞是最底下的節點才找到。

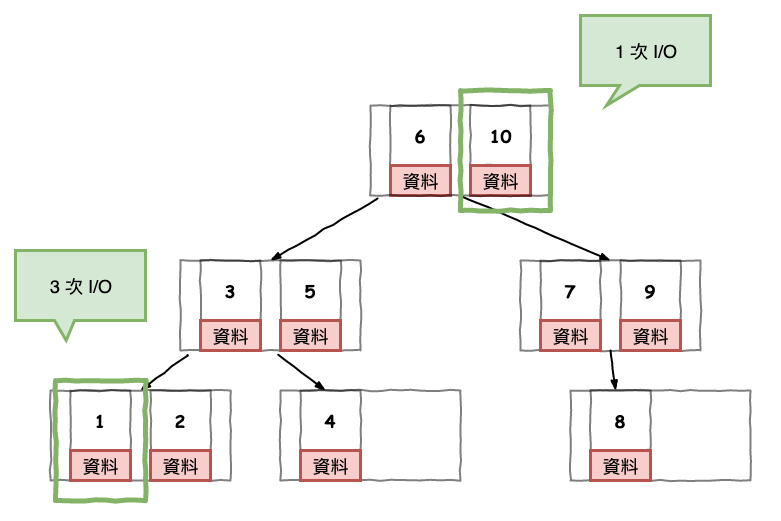
圖 10 : b 樹查詢不穩定問題

範圍搜尋時沒什麼效率

下圖 11 所示，假設咱們要找大於 2 的資料，那基本上就是所有的節點都會走一次，你可以算算幾次 i/o，下圖綠色線就是走的路。

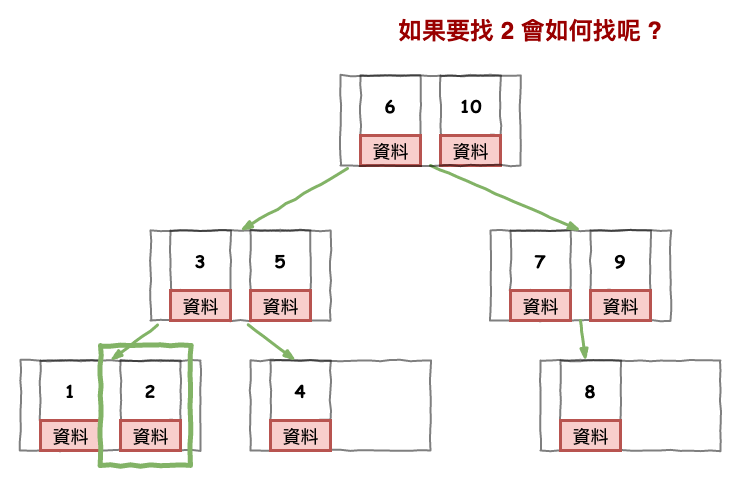
圖 11 : b-樹範圍搜尋時問題

節點太多 I/O 的問題

下圖 12 所示，如果咱們每個節點變大的話，那你覺得原本可以放兩個的，真的還可以放兩個嗎 ?

圖 12 : 資料變大問題

B+ 樹 ( Innodb 的選擇 )

b+ 樹是為了解決 b 樹的以下問題 :

查詢時不穩定、範圍搜尋時沒什麼效率、節點太多 I/O 的問題

假設我們有一顆 m 階的 b+ 樹，它和 b 樹相比，有以下幾個特點 :

• 每個節點，最多只能有 M 個子樹。
• 每個節點中的內部節點，最多只能有 M - 1 個。
• 每個非葉子節點(就是非最底層的節點)，只儲放索引用。
• 每個葉子節點(就是最底層的節點)，儲放了實際資料。
• 每個葉子節點(就是最底層的節點)，會包含一個指針，指向右邊的葉子即點。

根據以上的變化，b+ 樹大至上長的如下圖，有個小重點記一下 :

只有最下面的節點有資料，其它上面的節點只存索引

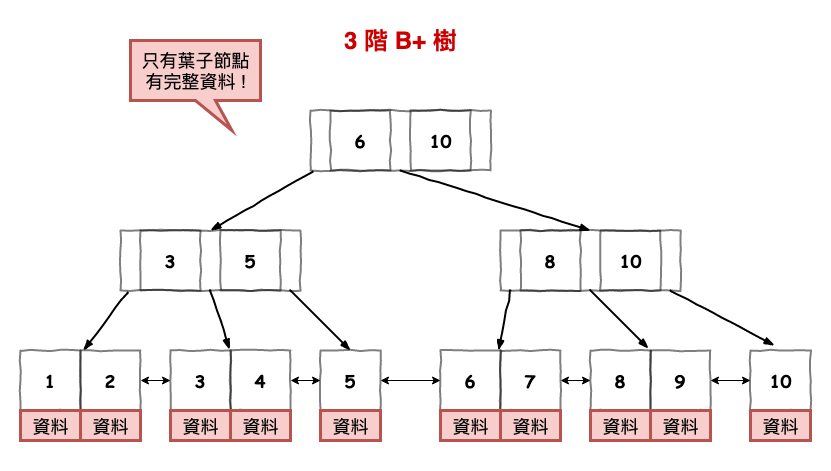
圖 13 : b+ 樹

B+ 樹的搜尋與範例搜尋流程

所以如果它要取得 5 的資料，那基本流程如下圖 14 所示，會 3 次 i/o，而如果你要找 6 實際上也是 3 次 i/o，這也代表所有節點搜尋的速度是平均的，而不會有快有慢。

而如果要找 5 的，也只要找到 5 以後，在一直往右抓資料就夠囉。

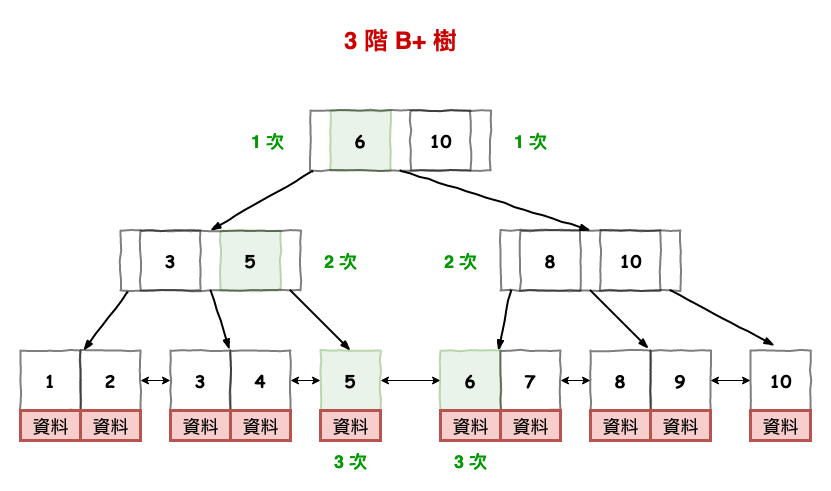
圖 14 : b+ 樹的搜尋範例

它與 B 樹的比較

• b+ 樹層級更少 : 主要的原因在於，非葉子節點 4 kb 的空間全部用來只儲指針，這也代表它有更多的空間來儲放。
• b+ 樹查詢更穩定 : 因為一定都要至葉子節點才能取得資料。
• b+ 樹自帶排序 : 因為它有用個鏈表，來依順序的葉子節點串起來。

結論與心得

本篇文章咱們從 0 至 1 的理解為什麼 innodb 要選擇使用 b+ 樹的原理，而這也是我們學習資料庫核心索引的第一步，當你理解以下，你就可以知道為什麼之後索引要這樣使用囉。

參考資料

• 平衡二叉树、B树、B+树、B*树 理解其中一种你就都明白了
• 面试题：InnoDB中一棵B+树能存多少行数据？
• 数据库索引为什么用B+树实现？
• B树和B+树的插入、删除图文详解