在模型更新時，我們可以利用 損失函數 (cost function) 來得到誤差，再來我們會根據這個函數的微分去做權重更新，而權重值更新的策略如何，就是看你使用了怎麼樣的優化器 (optimizer)，那這個優化器在 tensorflow 裡又該如何使用呢？且每個不同的優化器個代表什麼意義呢？今天來為大家介紹！

首先，我們假定要處理一個分類問題，所以會用 tf.nn.sparse_softmax_cross_entropy_with_logits ，作為損失函數，最前面程式碼我這樣規劃。

global_step = global_step = tf.train.get_or_create_global_step()

x = tf.placeholder(shape=[None, 2], dtype=tf.float32, name='x')
y = tf.placeholder(shape=[None], dtype=tf.int32, name='y')

with tf.variable_scope('backend'):
   net = tf.layers.dense(x, 64, activation=tf.nn.relu6, 
                               kernel_initializer=WEIGHT_INIT,
                               bias_initializer=BIAS_INIT,
                               kernel_regularizer=REGULARIZER, 
                               bias_regularizer=REGULARIZER, 
                               name='dense_1')
   net = tf.layers.dense(net, 64, activation=tf.nn.relu6,
                               kernel_initializer=WEIGHT_INIT,
                               bias_initializer=BIAS_INIT,
                               kernel_regularizer=REGULARIZER,
                               bias_regularizer=REGULARIZER, 
                               name='dense_2')
   logits = tf.layers.dense(net, 2, kernel_initializer=WEIGHT_INIT,
                               bias_initializer=BIAS_INIT,
                               kernel_regularizer=REGULARIZER,
                               bias_regularizer=REGULARIZER, 
                               name='final_dense')

loss = tf.reduce_mean(
   tf.nn.sparse_softmax_cross_entropy_with_logits(
       logits=logits, labels=y), name='inference_loss')

然後特別寫了一個方法來決定要使用哪種優化器。

def get_optimizer(opt_type):
   if opt_type == 'gd':
       return tf.train.GradientDescentOptimizer(learning_rate=0.1)
   if opt_type == 'momentum':
       return tf.train.MomentumOptimizer(learning_rate=0.1, momentum=0.9)
   if opt_type == 'ada_grad':
       return tf.train.AdagradOptimizer(learning_rate=0.1, initial_accumulator_value=0.1)
   if opt_type == 'rmsp':
       return tf.train.RMSPropOptimizer(learning_rate=0.1, decay=0.9, momentum=0)
   if opt_type == 'adam':
       return tf.train.AdamOptimizer(learning_rate=0.1, beta1=0.9, beta2=0.99)

在選定完優化器後，我們可以幫此優化器綁定 global_step，如此只要 train_op 執行過一次，不只會更新權重，同時也會自動幫 global_step 加一。

opt = get_optimizer(opt_type)

grads = opt.compute_gradients(loss)
train_op = opt.apply_gradients(grads, global_step=global_step)

再來，就是這次的資料集，為了方便 demo ，我寫了一個座標位置 xor 的方法來當測試，內容很簡單，他會產生 batch 為 16 的二維坐標，其座標值在 -1~1 之間 (遇到 0 就算了)，然後在第一和第三象限的座標結果值為 0，二和四象限的座標結果值為 1，兩行搞定。

def get_xor_data():
   x = (np.random.rand(16, 2) - 0.5) * 2
   y = [0 if 0 < x1 * x2 else 1 for x1, x2 in x]

   return x, y

我們訓練 100 次，並記錄所花費的時間，大家就可以自己比較各個不同優化器的收斂速度。

with tf.Session() as sess:
   sess.run(tf.global_variables_initializer())
   sess.run(tf.local_variables_initializer())

   start = timeit.default_timer()
   for _ in range(0, 100):
       x_v, y_v = get_xor_data()
       _, count = sess.run([train_op, global_step], feed_dict={x: x_v, y: y_v})

       print(f'iter: {count}')

   print(f'done. cost {timeit.default_timer() - start} sec.')

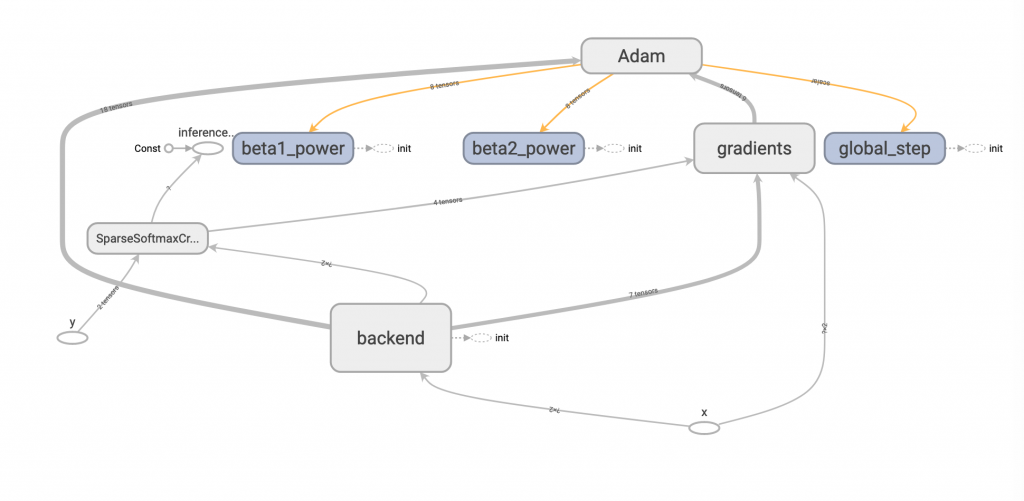
結果圖:

tensorflow 幫我們做了那麼多種優化器，用起來是很方便，但是你真的懂每個優化器使用時機嗎？沒錯，這次我也想挑戰以自己的話來解釋這幾種優化器的差異！

一、GradientDescentOptimizer

tf.train.GradientDescentOptimizer(learning_rate=0.1)

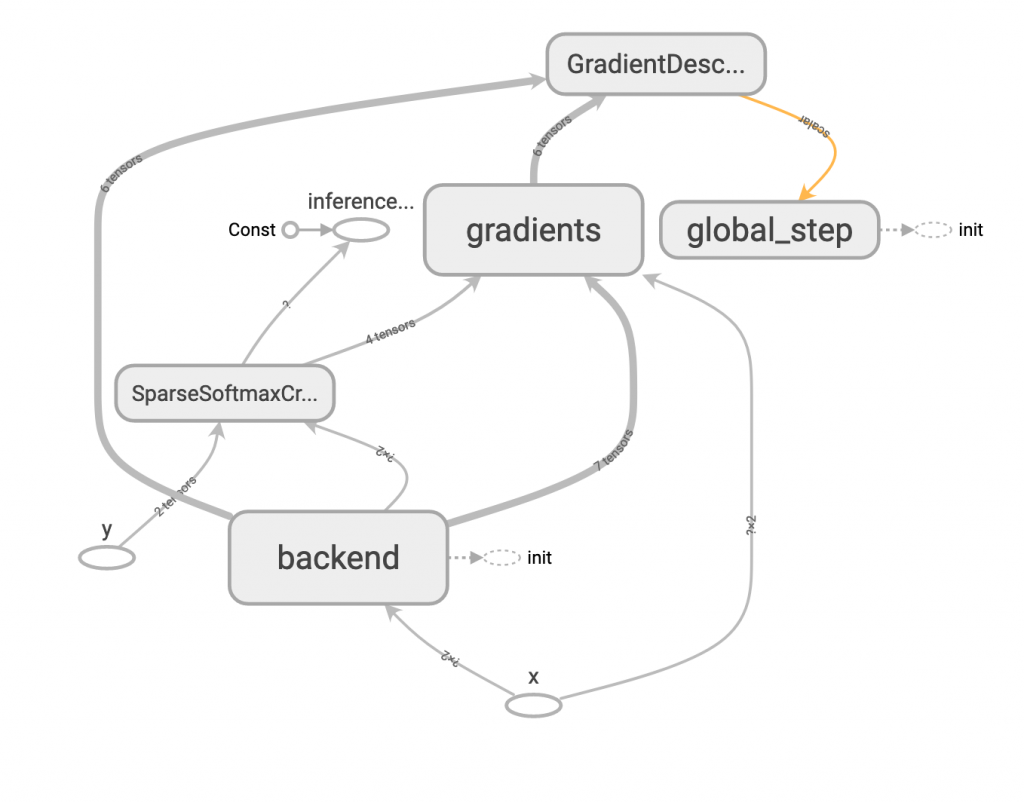
這個應該大家都知道，即最基本的 gradient descent，所需參數僅需要學習速度 learning rate。

對 cost function (以 J 表示) 的微分式子如下，t 表示某 step，theta 表示權重值。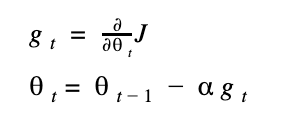

所以權重的更新就可以表示成(式子的 alpha 就是 learning rate)：

二、MomentumOptimizer

tf.train.MomentumOptimizer(learning_rate=0.1, momentum=0.9)

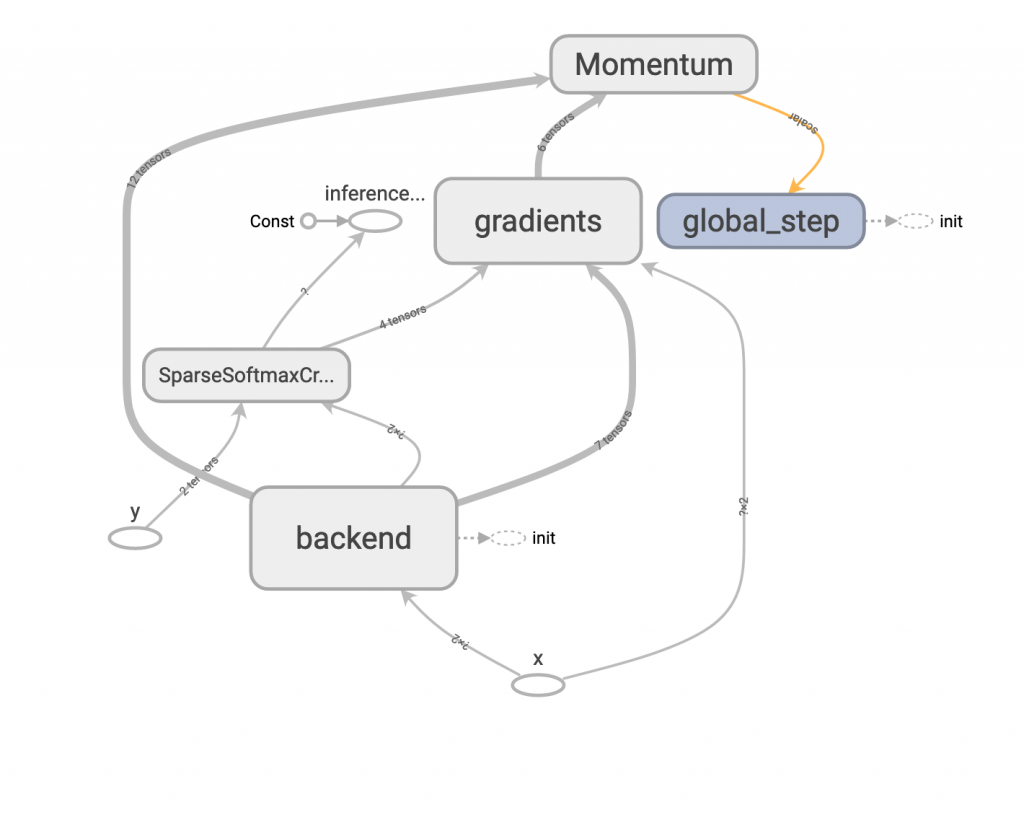
這個方法多了 momentum 這個參數，這個值通常設為 0.9 或 0.99，代表這次的更新量有多少部分是參考前一次的值，從公式上來理解可以比較清楚。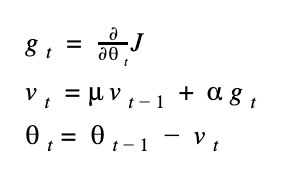

mu (很像 u 的符號) 表示 momentum 的參數值，v 表示目前更新值的大小，因此當模型開始訓練時，每次的更新量會被之前的更新量牽制，比較不容易忽大忽小，以增加穩定性。

三、AdagradOptimizer

tf.train.AdagradOptimizer(learning_rate=0.1, initial_accumulator_value=0.1)

這是以另一種想法來更新權重，我們用了一個會慢慢累加的快取 (cache)，來實作，我們將這個 cache 初始值設為 0.1 ，我們來看公式：

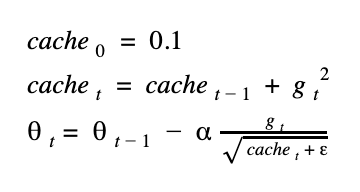
由於 gradient 的值會平方，所以保證 cache 一定是正數，可以放心開根號，但有些框架會預設把 cache 起始值設為0，那第一次迭代時，就有可能發生對0開根號的窘狀，所以會在公式中補個很小的 epsilon 來避免。
仔細想想，這樣的公式前其後和其會有什麼差異？訓練前期時，因為 cache 很小 又放在分母， gradient 除上這個值後會增大，因此更新量也大，訓練到後期時，cache 增大，gradient 除上大數字後，會讓更新量變小，因此牽制了後期的訓練量，使它越來越穩定。

四、RMSPropOptimizer

tf.train.RMSPropOptimizer(learning_rate=0.1, decay=0.9, momentum=0)

rmsprop 其實很簡單，它只比上面 adagrad 多了decay 的概念，所以有了 decay 這個參數，通常為 0.9 或 0.99，公式如下：

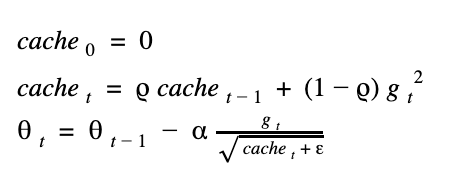
公式和 adagrad 幾乎一樣，只是多了一個 decay 值(這邊表示為 rho 很像 p 的符號)，那這個 rho 代表什麼意義呢？沒錯，它跟 momentum 很像，都代表著這次的 cache 值用多少部分的前一次的 cache 值加上這次的 gradient 值，設成 0.99 就是要用 99% 的前一次 cache 來更新。

而 tensorflow 的 API中多了 momentum 參數可以指定，其意義和前面介紹的 momentum 意思相同，但這邊為了專注解釋 rmsprop 所以就不多贅述。

五、AdamOptimizer

tf.train.AdamOptimizer(learning_rate=0.1, beta1=0.9, beta2=0.99)

如果讀者之前有讀過其他 adam 有關的教學，八成都會提到 adam 是 momentum 加 rmsprop 兩者的方法，呃...在這邊我想說的是，這並不那麼精確，如果是這兩種方法的總和，那上面 tensorflow 的 RMSPropOptimizer 就已經有 momentum 可以用了。那話說回來，這和 adam 有什麼不一樣的地方呢？那就是 adam 多了 bias corrections 這個用法，我們慢慢分解公式。

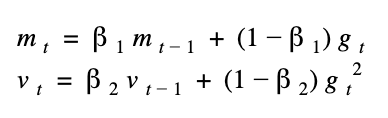
前面提到的 momentum 和 rmsprop 個別都有參數 mu 和 rho 的 decay 概念來控制，在 adam 中，我們個別將其改名 beta1 和 beta2，然後又因為這個公式很剛好又可以被表示成統計學的一二級動差，所以我們換成 mean (公式中的m)和 var (公式中的v)來表示。

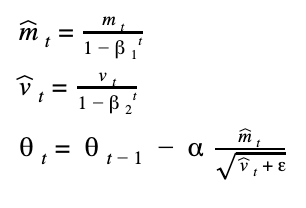
上面戴帽子m 和帽子v 就是經過 bias corrections 的參數，如果你觀察 bias corrections 的公式，可以發現初期 t 很小時，beta1 和 beta2 會把 m 和 v 校正成比較大的參數，以便放大初期的學習效果，等到訓練到後期時，t 慢慢變大，因為 beta1 和 beta2 兩個都是小於1的參數，經過多次方後會超級小，最後根本帽子m 和帽子v 等同於原本的m 和 v (即不校正)，所以更新又會趨緩讓模型變得穩定。

看完以上五種方法，大家應該有發現不管哪種方法，都是希望訓練初期可以讓模型走大步一點以加速收斂，直到訓練中後期再慢慢趨緩，避免損失震盪。

呼！為了這篇文，我在 google doc 打了好久的公式，這是我很用心的一篇，自己也花了不少時間把網路上零散的知識一次整理好，如果喜歡還請按個讚，也歡迎提問！

github原始碼