前言

十幾年前到電信公司工作時，接到的第一個專案就是要幫客服中心安排人力班表，我們調查過很多國內外的WFM(Workforce Management)系統，通通不合用，當時應該也沒有一家電信公司有解決方案，大都是憑藉客服主管的經驗安排值班人力，同時利用彈性工時的兼職人員填補人力缺口，在既定的服務品質(service level agreements, SLA)條件下，希望做到人力成本最小化。

以下我們就將問題簡化，介紹『線性規劃』(Linear Programming)如何解決值班人力排程的問題。

問題描述

人力規劃(Workforce Planning) 基本上是一個優化(Optimization)的問題，舉一個簡單的例子如下：

1. 每天各時段的話務量會波動，如下圖：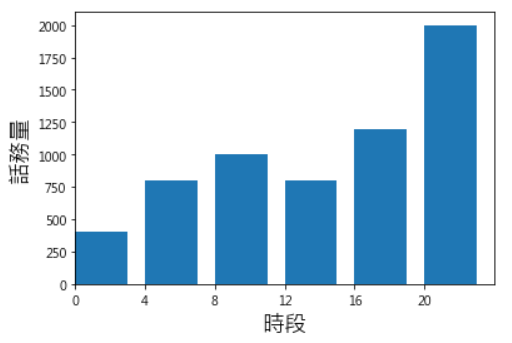
   
   圖. 每天各時段的話務量

2. 每人每天值班8小時。

3. 話務量 = 總通話時間 / 每個客服人員(Agent)的平均服務時間。

請問各時段至少要安排多少人力? 以下我們先介紹線性規劃的概念，之後再實際求解此一問題。

線性規劃(Linear Programming)

線性規劃是利用優化的技術，求取目標函數的最大值或最小值，除了定義目標函數以外，通常還會有一堆的限制條件，例如，每人每天最多值班8小時、每個時段的人力安排須大於需求，因此，可以數學式表示如下：

圖片來源：Python | Linear Programming in Pulp

上述問題可以使用 pulp 或 scipy 套件求解，pulp安裝指令如下：

pip install pulp

程式如下：

# import the library pulp as p 
import pulp as p 

# 建立線性規劃 求取目標函數的最小值
Lp_prob = p.LpProblem('Problem', p.LpMinimize) 

# 宣告變數(Variables)
x = p.LpVariable("x", lowBound = 0) # Create a variable x >= 0 
y = p.LpVariable("y", lowBound = 0) # Create a variable y >= 0 

# 定義目標函數(Objective Function)
Lp_prob += 3 * x + 5 * y 

# 定義限制條件(Constraints) 
Lp_prob += 2 * x + 3 * y >= 12
Lp_prob += -x + y <= 3
Lp_prob += x >= 4
Lp_prob += y <= 3

# 顯示問題的定義
print(Lp_prob) 

# 求解
status = Lp_prob.solve() # Solver 
print(p.LpStatus[status]) # The solution status 

# 顯示答案 
print(p.value(x), p.value(y), p.value(Lp_prob.objective)) 

執行後答案如下：

1. x=6
2. y=0
3. 目標函數的最小值=18

接著，我們就來求解客服人力規劃的問題。

客服人力規劃

假設每4個小時為一時段，x0代表0~4點的值班人數，x4代表4~8點的值班人數，以此類推，x20代表20~24點的值班人數，所以，定義
目標函數： x0 + x4 + x8 + x12 + x16 + x20
限制條件：
x20+x0>=400
x0+x4>=800
x4+x8>=1000
x8+x12>=800
x12+x16>=1200
x16+x20>=2000
程式如下：

# import the library pulp as p 
import pulp as p 

# 建立線性規劃 求取目標函數的最小值
Lp_prob = p.LpProblem('Problem', p.LpMinimize) 

# 宣告變數(Variables)
x0 = p.LpVariable("x0", 0,None,p.LpInteger) # Create a variable x >= 0 
x4 = p.LpVariable("x4", 0,None,p.LpInteger) # Create a variable x >= 0 
x8 = p.LpVariable("x8",0,None,p.LpInteger) # Create a variable x >= 0 
x12 = p.LpVariable("x12",0,None,p.LpInteger) # Create a variable x >= 0 
x16 = p.LpVariable("x16",0,None,p.LpInteger) # Create a variable x >= 0 
x20 = p.LpVariable("x20",0,None,p.LpInteger) # Create a variable x >= 0 

# 定義目標函數(Objective Function)
Lp_prob += x0 + x4 + x8 + x12 + x16 + x20

# 定義限制條件(Constraints) 
Lp_prob += x20+x0>=400
Lp_prob += x0+x4>=800
Lp_prob += x4+x8>=1000
Lp_prob += x8+x12>=800
Lp_prob += x12+x16>=1200
Lp_prob += x16+x20>=2000

# 顯示問題的定義
print(Lp_prob) 

# 求解
status = Lp_prob.solve() # Solver 
print(p.LpStatus[status]) # The solution status 

# 顯示答案 
print('x0={}'.format(p.value(x0)))
print('x4={}'.format(p.value(x4)))
print('x8={}'.format(p.value(x8)))
print('x12={}'.format(p.value(x12)))
print('x16={}'.format(p.value(x16)))
print('x20={}'.format(p.value(x20)))

print('需求總人數={}'.format(p.value(Lp_prob.objective)))

執行後答案如下：
0~4點的值班人數=0.0
4~8點的值班人數=800.0
8~12點的值班人數=200.0
12~16點的值班人數=600.0
16~20點的值班人數=600.0
20~24點的值班人數=1400.0
需求總人數=3600.0

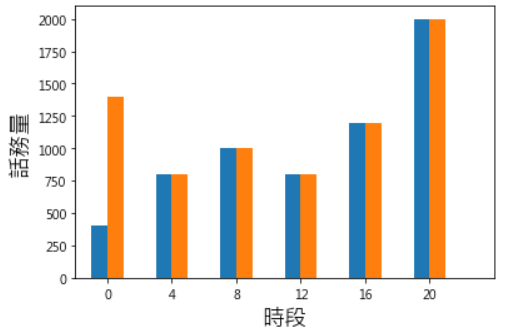
圖. 需求與供給的比較

除了0~4點，所有時段的排班需求與供給都完美的匹配，這時，我們就可以彈性工時的人力調節0~4點的供給，進一步調整人力，再壓低人力成本。

結語

當然，上述的問題過於簡單，真正的現場還會有很多的限制，例如勞基法的規定、用餐時間的安排、HR的考量、辦公設備及空間的限制、資源撫平等等，這時就需系統分析師動動腦，想想對策了。

有關人力規劃(Workforce Planning)的應用非常廣泛，不只使用在客服中心，包括電銷中心、運輸業人力調度、工廠輪班、倉位安排等等的資源分配問題，都可以利用線性規劃處理。