在評估模型的時候,會發現模型與結果有誤差,模型無法針對我們的測試集反映出真正結果,這就是評估的偏差(evaluating for bias)。這時候就是需要用到混淆矩陣(confusion matrix)來評斷這個模型。
文章:Fairness: Evaluating for Bias
當我們模型訓練出來後,評估該模型的真實狀況,會使用混淆矩陣(confusion matrix)。他是一個工具,用來檢查模型預測結果的工具,借此我們可以了解「預測」與「真實」的關係性。
這個矩陣是為2*2的格式,分成「預測的類別」和「實際的類別」:
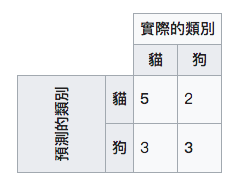
當我們使用這個樣本是對的時候,模型也是預測為對,這就是右上角的TP,預測和事實相同;但是當模型預測為錯的時候,就是錯誤的正向預測,也就是右上角的部份。當使用的樣本是錯的時候,模型預測為錯,表示正確的反向預測,所以就是在右下角;相反的為模型認為是對,這就是錯誤的正向預測。結果就是如下表:
| x | 實際分類 | 實際分類 |
|---|---|---|
| 預測分類 | TP(True Positive) | FP(False Positive) |
| 預測分類 | FN(False Negative) | TN(True Negative) |
而我們的目標就是在「true」的地方多,「False」的地方少,當錯誤的太多,表示這個模型是不能使用的。
要比較的方式,比較常用的是:Precision(準確率)和Recall(召回率)。根據如何辨別機器學習模型的好壞?秒懂Confusion Matrix所說「Precision看的是在預測正向的情形下,實際的「精準度」是多少,而Recall則是看在實際情形為正向的狀況下,預測「能召回多少」正向的答案」。以Fairness: Evaluating for Bias的例子來說,進行評估是否有腫瘤使用1000個患者的醫療記錄,其中500男人,500女人,可以得到這樣的陣列:
| x | 實際有腫瘤 | 實際沒腫瘤 |
|---|---|---|
| 預測有腫瘤 | 16 | 4 |
| 預測沒腫瘤 | 6 | 974 |
而Precision(準確率)是: (TP)/ (TP + FP),所以是16/20=0.8;Recall(召回率)則是:(TP)/ (TP + FN),因此為16/(16+6)=0.7272。這個數據看起來準確度很高,感覺這個模型可以使用。為了保險起見,分別拿這個模型給男人和女人去驗證。
| x | 實際有腫瘤 | 實際沒腫瘤 |
|---|---|---|
| 預測有腫瘤 | 10 | 1 |
| 預測沒腫瘤 | 1 | 488 |
| x | 實際有腫瘤 | 實際沒腫瘤 |
|---|---|---|
| 預測有腫瘤 | 6 | 3 |
| 預測沒腫瘤 | 5 | 486 |
其中女人的準確率為:10/(10+1)=0.9090,召回率為:10/(10+1)=0.9090。
反而男人的準確率為:6/(6+3)=0.6667,召回率為:6/(6+5)=0.5454。
這樣看起來,女性大概有9.1%的人不會被預估到有腫瘤,而男性卻有33.3%的機率不會被檢測到,有45.45%機會被誤判。因此這個模型只有女性的預估是準的,男性的狀況有點慘。
因此可以用這個混淆矩陣(confusion matrix)的方式評估該模型的狀況,理解是否有偏差。
參考資料:
睫毛之聲:
除了資料開始時的偏差,連結果也會有偏差,果然做數據的時時刻刻都要盯著數字,不然失之毫釐,差之千里。
也在本篇發現混淆矩陣(confusion matrix)這個方式還滿好用的!![]()
