前言

昨天我們簡單介紹了Reinforcement Learning的緣由，
今天內容為貫穿整個Reinforcement Learning的要素：Markov Decision Processes(MDP)，
每個強化學習的算法皆會遵循此一過程，非常重要！

多臂老虎機(Multi-armed bandit)

回想一下昨天的小白鼠實驗，我們訂下一個timestep用來作為行為前的時間點，每個時間點都有
(按按鈕)跟(不按按鈕)兩種行為，我們與環境互動的過程就像下面這張圖

而這種問題其實就是一種Multi-armed bandit(多臂老虎機)的問題，在時間點做一個行為，得到回饋。而我們目的就是將每個行為得到的Reward都最大。

但這種多臂老虎機的模型能夠概括所有強化學習的情境嗎？其實不行，多臂老虎機只是強化學習中的一小部分。那強化學習與多臂老虎機的差別在哪裡呢？就是多了個紀錄狀態的State，在現實生活中，我們每一個不同的State，都會影響我們接下來的Action。想像我們現在要學習玩井字棋，有以下兩種State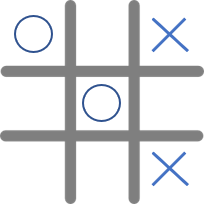

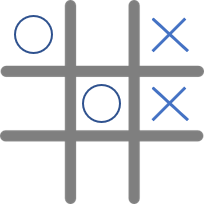
當我們的Agent(圈方)看到這兩種情況，應該要做出不同的決策才能獲勝，但在多臂老虎機中，我們不需要觀察目前的State，也就是說我們可以把多臂老虎機視為只有一個State的特殊情況。

馬可夫決策過程(Markov Decision Process)

在強化學習中，我們已經學到三個基本元素

1. State
2. Action
3. Reward

這三個元素就是我們的Agent與Environment互相溝通的訊息，但是我們還缺少了溝通的管道。這個管道就是透過Markov Decision Process(MDP)這個數學模型。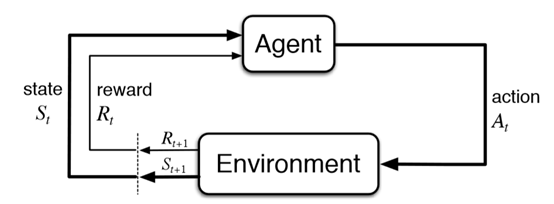

從上面這張圖可以看到Agent與Environment是怎麼互動的。Environment會給出時間點的State和Reward給Agent，Agent再從這些資訊中決定要做出甚麼行為，Environment再透過Agent的行為中決定下個時間的State和Reward。

你可能會想問：幹嘛要特地搞一個新的數學模型出來，用簡單的State Machine不就可以了。其實MDP還有以下兩種特性：

1. 所有的過程都有隨機性
2. 下一個狀態轉移只與現在這個狀態有關

先看第一點，在現實生活中，我們不能預測未來會發生甚麼事情，就算我們在時間點根據做了行為，下個時間點的狀態卻是不確定的，我們說這個環境轉移的機率為MDP的Dynamic，用數學式子表達就是 。

此機率為條件機率，可以看成在狀態時做出行為後，下一個狀態為且獎勵為時的機率。

繼續井字棋的例子，我們只能猜測對手的行為，根據對手行為的機率來決定我們的行為。這也是強化學習在現實中難以拓展的原因之一，因為現實生活中的Dynamic的變化太大，很難正確的預估未來的狀態。

第二點稱為Markov Property，是MDP的一個重要特性。可以從下面的數學式子理解

白話一點就是現在的狀態包含著過去經歷過的所有狀態的資訊。也就是說，我們所求的機率，可以捨去過去的所有狀態，只專注於眼前的狀態。這大大幫助我們減少計算量，且能夠用簡單的迭代法來求出結果。

不是所有Reinforcement Learning的問題都滿足Markov Property，但是我們可以假設滿足Markov Property來達到近似的結果

還有一點需要特別注意的是，加入State的因素後，我們要考慮的就不是當前的Reward，而是後續所有的Reward，如同昨天所說的。一樣用井字遊戲的例子，假如我們訂下當連續兩個圈連在一起時，Reward = 1；贏了遊戲Reward = 5；輸的話Reward = -5。現在情況是是這樣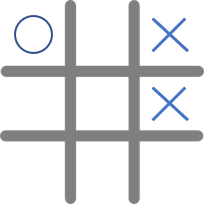

我們Agent(圈方)如果為了要獲得目前最大的Reward，他會選擇左上角三個空格，很明顯是不合理的行為。所以MDP與多臂老虎機不同的地方是，我們最大化的目標必須是。

總結

現在我們已經討論完所有強化學習的要素，簡單統整一下分為

• 狀態 State，
• 動作 Action，
• 獎勵 Reward，
• 轉移機率 Dynamic，

這邊Action的空間範圍是依照State來決定，因為每個狀態可以做的行為不一定都一樣。
事實上，除了State外，回饋的Reward也可能存在隨機性，所以Dynamic可以拆成兩部分

且必須滿足機率的條件

看到這裡其實已經把Reinforcement Learning的架構都學會了，剩下的只是套用算法來想辦法透過action讓得到的所有Reward最大化，明天應該會介紹Policy與bellman equation來解這些問題~