前言

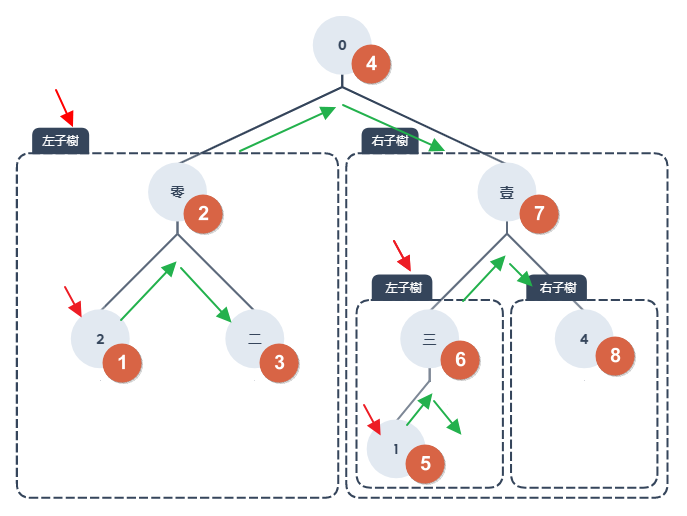
對中序走訪有初步了解之後，要來介紹難度高一點點的前序走訪，其實走訪概念是雷同的，差別在於順序不同，還有走訪結果人腦不容易判讀，但方便電腦`進行判讀

生活常識

昨天我們提到的常用的計算機，在進行加法或減法時十分方便，但你有遇過乘法或除法的情況嗎？例如 1 + 2 + 3 * 2，你覺得計算結果是9還是12呢？答案是9，因為四則運算中有一個原則是先乘除後加減，所以我們會習慣先進行 3 * 2 = 6 的部分，再將 1 + 2 + 6 就會得到 9，那如果你想要得到 12，那你的算式必須使用括號，公式為 ( 1 + 2 + 3 ) * 2 = 12

之前有一道小學生程度的題目很紅，聽說大概有 4 成的人都答錯(包括我)，請問你知道下列算式的答案會等於多少嗎？

6 ÷ 2 ( 1 + 2 ) = ?

有人覺得答案是 1 ，有人覺得答案是 9 ，哪一個是你心目中的答案呢？中序式很容易讓人類判讀，但像這樣的小學生題目，竟然也會有 4 成的人答錯，這樣人腦的可信度似乎沒有想像中的高，所以有時候還是要靠電腦來輔助驗算正確與否

而這題正確答案是 9 ，試著把括號寫出來就很清楚了，因為我們都知道括號的地方要先運算：

• 答案 9 的公式
  ( 6 ÷ 2 ) * ( 1 + 2 ) = 9

• 答案 1 的公式
  6 ÷ ( 2 * ( 1 + 2 ) ) = 1

但題目並沒有給這麼多括號，所以要怎麼辦，到底是 9 對還是 1 對呢？當題目沒有明確給出括號時，那就是由左往右計算，另外記得題目有給括號的地方要先算：
　6 ÷ 2 ( 1 + 2 )
= 6 ÷ 2 ( 3 )
= 3 ( 3 ) = 9

專業知識 - 二元樹前序走訪 Preorder

接著我們來看一下，如果今天是請電腦計算6 ÷ 2 ( 1 + 2 )這一題，會不會答對呢？

前序走訪 Preorder

複習一下昨天提到的前序走訪的順序：根節點 → 左子樹 → 右子樹，根節點在前面，結果為：根左右，左子樹的順序一定會大於右子樹，重點就在於根節點的位置在哪邊

例如：中序式的3 + 5，使用前序式表達的話會變成 + 3 5 ，表達式：< 運算子 > < 運算元1 > < 運算元2 >

前序練習

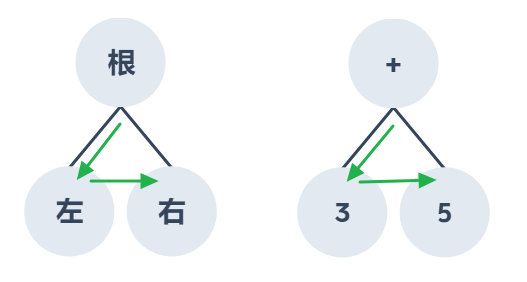
中序式公式：6 ÷ 2 ( 1 + 2 )

先將二元樹畫出來，如下圖，如果不懂二元樹數如何畫出來的，可以使用以下兩個小技巧：

1. 將公式的括號配對好，記得明確將要先加減或後乘除的地方括好
   例如：( ( 6 ÷ 2 ) * ( 1 + 2 ) )

2. 配對原則就是兩個數字(左右節點)搭配一個四則運算(數根)

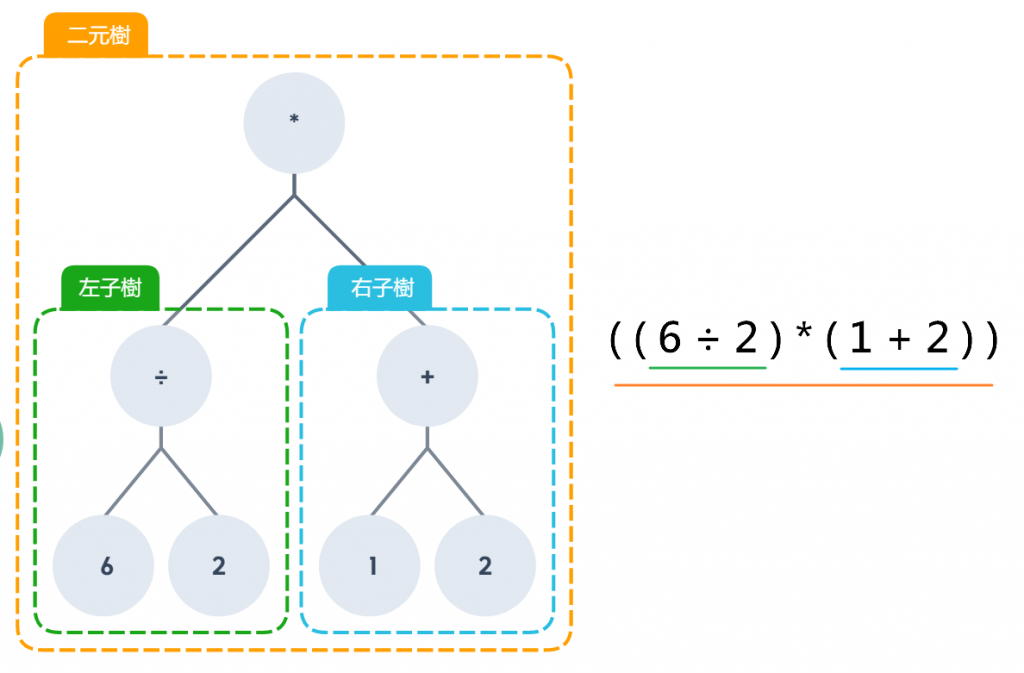
再來我們要使用前序走訪，取得走訪結果，要先從樹根開始訪問，順序：根節點 → 左子樹 → 右子樹，如果樹根結點下面有子樹，則繼續往該子樹的樹根往下訪問，先處理左子樹，再處理右子樹

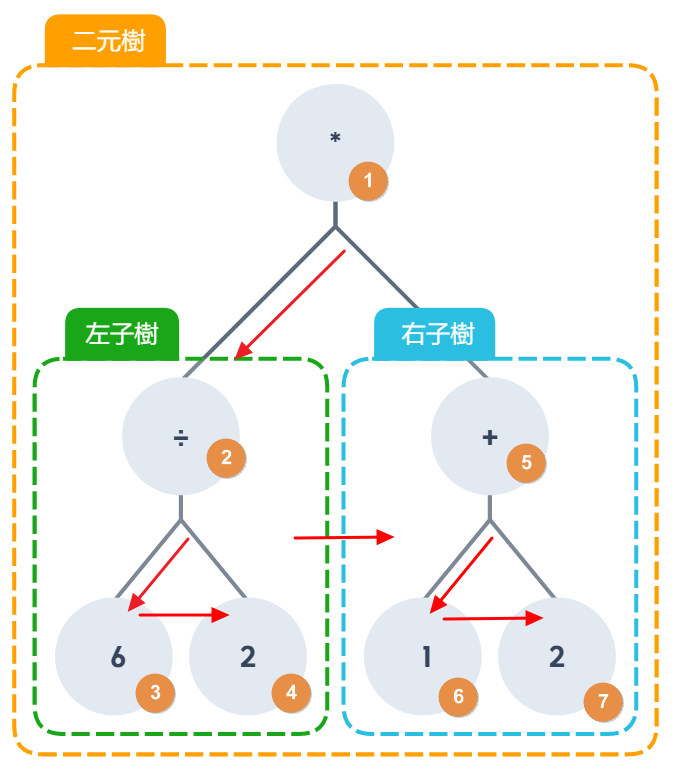
最後的前序走訪結果為：* ÷ 6 2 + 1 2，這時候電腦就可以開始進行運算，讀取順序為由右往左，讀取資料的規則為：連續 2 個數字與 1 四則運算就會開始計算：

走訪結果與電腦計算過程：

• ÷ 6 2 + 1 2
  一開始會先讀取到+ 1 2，電腦就會進行 1 + 2 = 3 的運算

• ÷ 6 2 3
  接著會讀取到 6 2 3，但不符合連續 2 個數字與 1 四則運算的規則，所以繼續讀到÷ 6 2，電腦就會進行 6 ÷ 2 = 3 的運算

• * 3 3
  然後繼續由右往左讀取* 3 3，電腦就會進行 3 * 3 = 9 的運算

• 9
  最後就會得到答案 9 囉

今日小結

透過前序的走訪結果，是不是有觀察到，電腦在運算過程中完全不需要考慮括號與先乘除後加減的問題，只要按著由右而左，且讀取到連續 2 個數字與 1 四則運算時再進行運算即可，另外在電腦實際計算時，透過程式實作還須要透過堆疊才能成功取得連續 2 個數字與 1 四則運算，這個部分會在日後講演算法時會在討論到

今日謎題

你獲得加入超人團隊的機會，你必須通過考核才能加入，因為了預防機密外流，通訊過程都會使用二元樹前序訪問的方式，請問你能成功解密嗎？內容為一個單字

昨日解謎

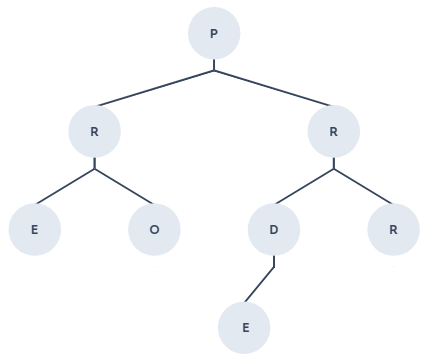
謎題說明：使用中序走訪(Inorder)：順序：左子樹 → 根節點 → 右子樹，如果遇節點下面還有左子樹，那就要先走訪最下層的左子樹，要記得左子樹的優先權永遠大於右子樹，處理完畢之後在再處理根節點，最後才是處理右子樹，走訪順序可參考下圖橘色圈圈的數字，數字由小到大看過去的話，最後結果就會得到：2零二01三壹4，所以小美男朋友是想告訴小美：愛你愛你一生一世，你猜到了嗎？