昨天在研究MDS的時候順便把PCA也複習了一下，所以今天來把它相關的原理補上（非常推薦觀看reference的影片呦，大概是我看過PCA講解得最清楚的！），PCA是另一種把高維度資料轉化成低維度資料的方法，讓我們將本多維度的資料視覺化。

PCA原理

主要利用“線性”辦法降維，也就是降維生成的每一個PC都是原本變數（x1,x2,x3...）的線性組合，因為是線性組合，我們也可以透過beta對應到哪一些變數是比較有用的，比如 PC1=0.8x1+0.25x2，由於0.8>0.25，可以知道x1為主要成份並有較大的影響。

那PC是如何生成的呢？
假設我們現在有一個實驗室資料集，我們想知道老鼠間基因的相似程度（gene1,gene2)，我們先把資料畫出。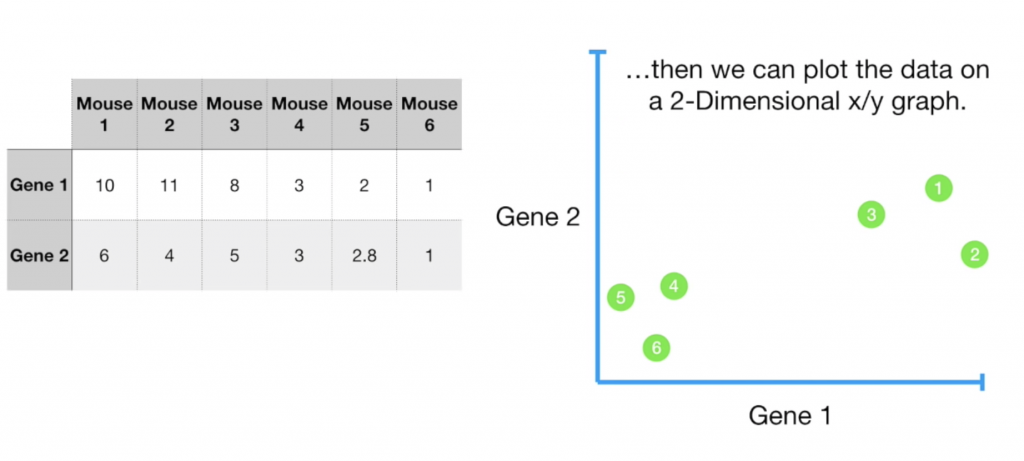

接著移動資料，將中心點調整至（0,0)，並找出一條通過原點的線，讓每個點到這條線的平方距離最小，這條線就會是我們的PC1，而PC2就是垂直於PC1的線，若有PC3，則為一條垂直於PC1與PC2的線，依此類推。

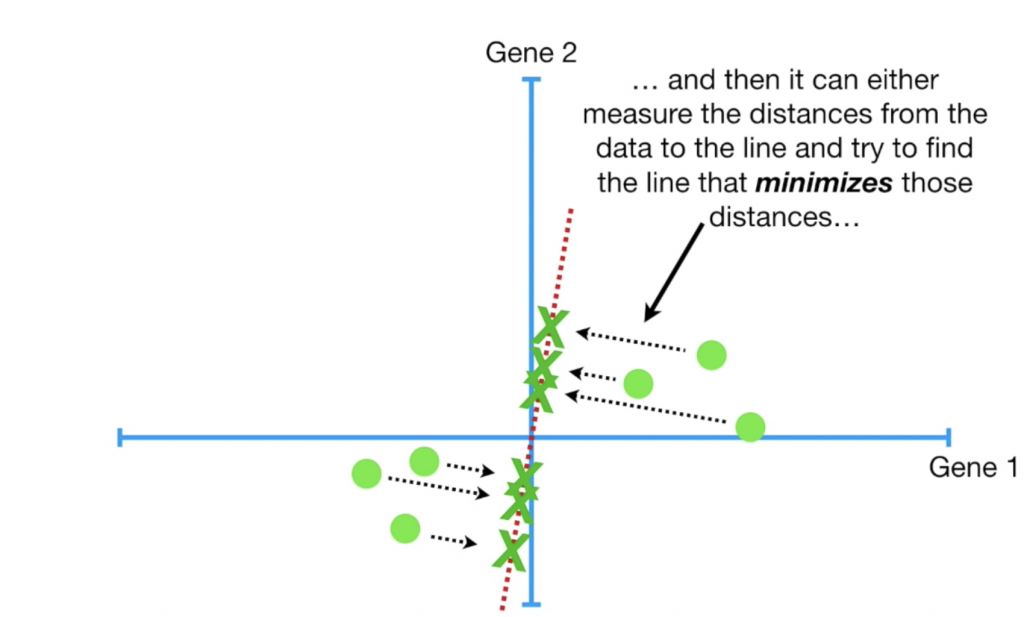
在實際計算中，其實pc計算距離時並不是計算min(點到線的距離平方和)，而是計算max(點投影在線上之後到原點的距離平方和)（eigenvalue)，我們可以用簡單的畢氏定理知道這是同一件事：當a固定，想求出最小的b等同於球出最大的c。

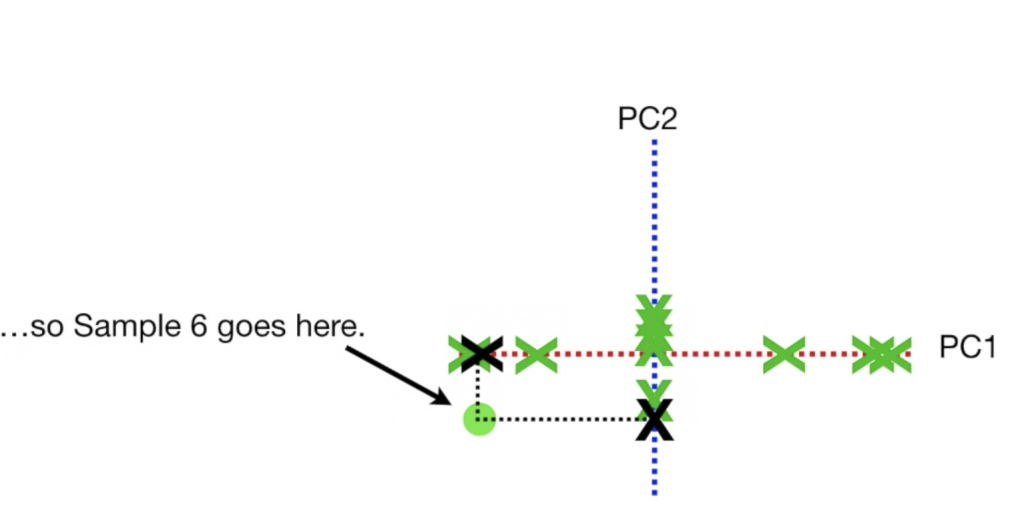
最後呈現的圖，就是把圖旋轉，讓PC1為x軸，PC2為y軸，再把資料點根據投影在兩條線上的位置畫出對應位置：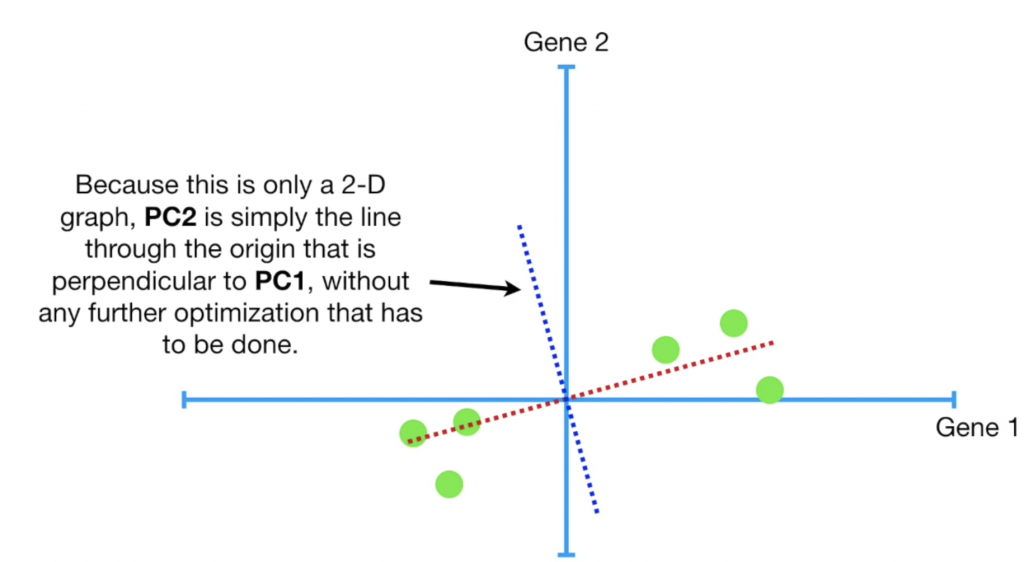

想要降成幾個維度呢？看看variance

另一個常見的問題是要將資料將成幾個維度，就像是k-mean cluster要定義的k一般，這時候我們可以看看每個pc解釋了多少資料離散程度，variance公式為 eigenvalue/（n-1），加總所有PC的variance並算出每個PC解釋的比例，解釋比例越高代表PC越有效（通常variance解釋比例會逐漸下降），我們可以由此找出想要的PC數量，比如總共有5個PC，但PC1,PC2已經解釋95%的離散，那選擇2個PC就可以很好的表達資料並不需要再增加。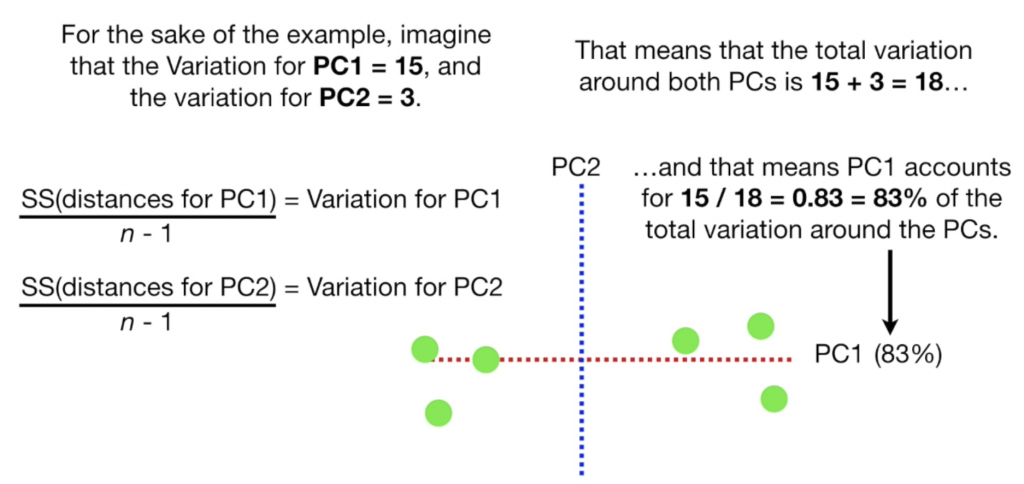

Python

我們一樣用昨天iris dataset來舉例：

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.manifold import MDS
from sklearn.preprocessing import MinMaxScaler

data = load_iris()
X = data.data

scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca = pca.fit_transform(X_scaled)

pca_df = pd.DataFrame(data = pca,columns = ['pc1', 'pc2'])
pca_df['target']=data.target

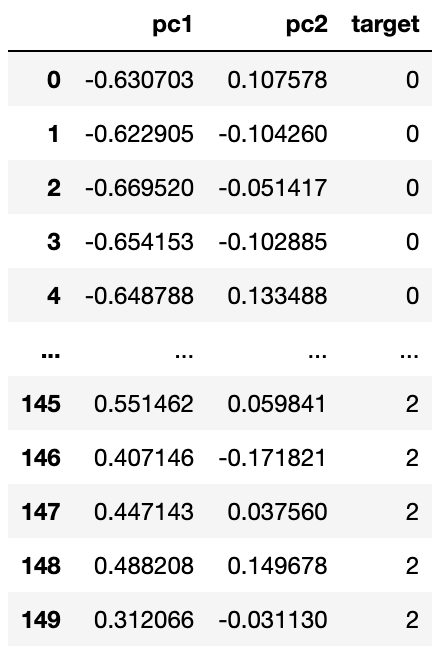
fig = plt.figure(figsize = (5,5))
ax = fig.add_subplot(1,1,1) 

targets = [0, 1, 2]
colors = ['r', 'g', 'b']
for target, color in zip(targets,colors):
    indices = pca_df['target'] == target
    ax.scatter(pca_df.loc[indices, 'pc1']
               , pca_df.loc[indices, 'pc2']
               , c = color
               ,label=data.target_names[target])
ax.legend()
ax.set_xlabel('Principal Component 1', fontsize = 15)
ax.set_ylabel('Principal Component 2', fontsize = 15)
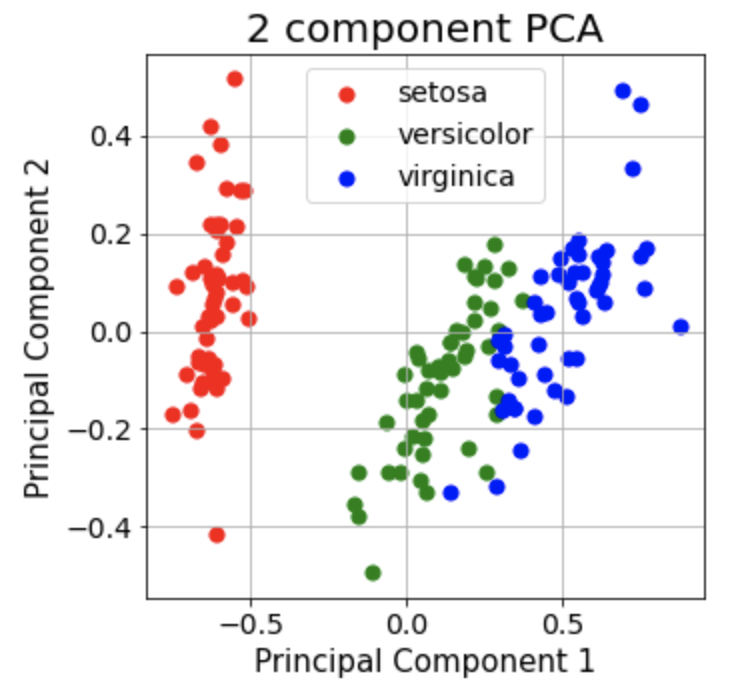
ax.set_title('2 component PCA', fontsize = 20)
ax.grid()

pca.explained_variance_ratio_

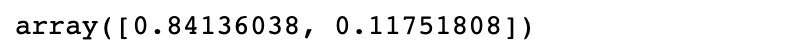
references:
https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html
https://www.youtube.com/watch?v=FgakZw6K1QQ