今天想來談談一個把高維度資料可視化的應用：MDS，MDS是一種unsupervised machine learning approach 用來降低資料的維度，也有另一個說法叫做Principal Coordinate Analysis(PCoA)。

MDS原理

當MDS要把高維的資料降低成低維度時，會確保樣本間的距離保持不變，而如果今天我們把維度降為2，那我們就可以把降維樣本畫出2D圖像來看分佈情形。可以應用在偵測資料有沒有outliers，或是在做cluster之前也可以先畫MDS看看資料分布。

MDS主要的原則是保持“距離”不變，但這裡的距離是可以變換的，我們可以使用最簡單的euclidean distance，也可以使用第一天提到的DTW，要注意的是如果使用euclidean distance，跑出的分佈結果會和PCA相同。另外一個要注意的地方是因為牽涉到距離，所以要執行MDS的資料必須要先標準化（normalization）。

Python

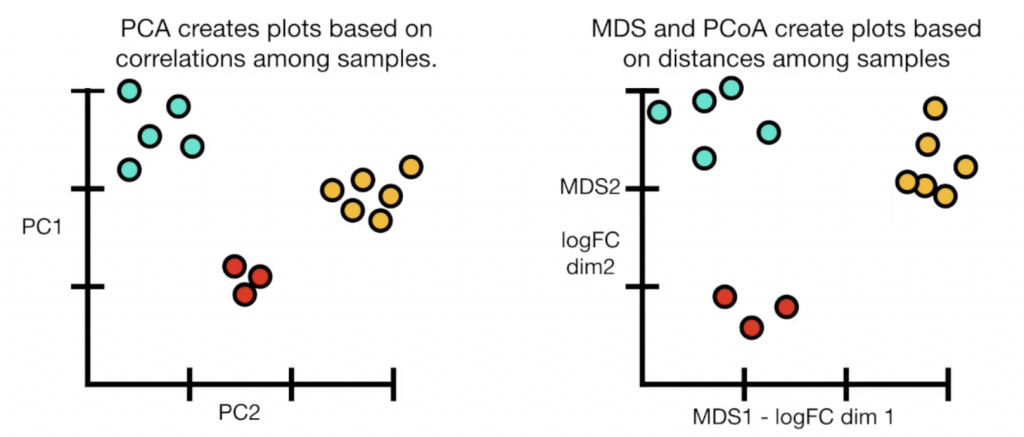
來用有名的iris dataset舉例：

import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.manifold import MDS
from sklearn.preprocessing import MinMaxScaler

data = load_iris()
X = data.data

scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)

MDS的重要參數有：

1. n_components：想要降低成幾維度的資料
2. dissimilarity（default=’euclidean’）：若要放入別的distance metric則輸入‘precomputed’，並在fit_transform語法中放入metric

mds = MDS(n_components=2,random_state=0)
X_2d = mds.fit_transform(X_scaled)

colors = ['red','green','blue']

for i in np.unique(data.target):
    subset = X_2d[data.target == i]
    x = [row[0] for row in subset]
    y = [row[1] for row in subset]
    plt.scatter(x,y,c=colors[i],label=data.target_names[i])
plt.legend()
plt.show()

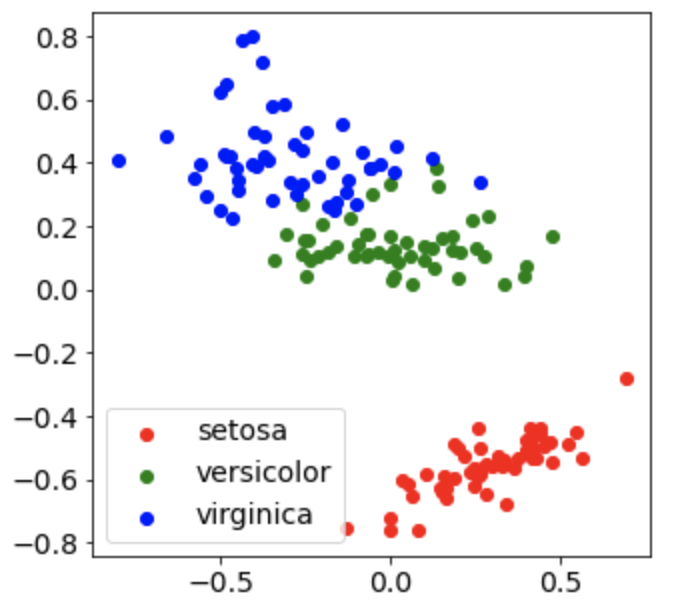
最後要注意的是，上圖中的x與y軸能代表每個資料轉換後的座標，並沒有實質上的解讀意義呦！

references:
https://www.youtube.com/watch?v=GEn-_dAyYME
https://towardsdatascience.com/visualize-multidimensional-datasets-with-mds-64d7b4c16eaa
https://scikit-learn.org/stable/modules/generated/sklearn.manifold.MDS.html