今天來聊聊在ML裏面一天到晚聽到的gradient descent!
Gradient descent是用來解決Optimization問題的常見算法，也因為只是一個計算的方式，透過變換不同的Loss function，gradient descent可以應用在很多不同的場景中。

原理

想了解gradient descent首先要先知道一點點微積分的概念，基本上只要知道一階微分還有微分其實就是斜率這兩件事就可以了（笑，主要的步驟有：

1. 對你的loss function做微分：看有幾個參數就對個別參數做一次偏微分，你偏微完的東西就叫gradient
2. 對參數隨機設置起始值：你可以說剛開始大家都是0，或是任何數字
3. 計算slope: 把你設定的參數值放進你的gradient裏算出的就叫slope
4. 計算step: step=slope * learning rate
5. 計算新的參數值：等於舊的參數值-step
6. 重複步驟3-5直到你的slope/step趨近於0

只看上面的步驟可能覺得我不知道在說什麼，這邊舉一個簡單的例子：如果我們今天有一個3個資料點的dataset，我們想要找出一條最好的線來表現（y=ax+b)，在這裏為了簡化我們假設已知a=0.64，所以目標是找出最理想的b，這裡的loss function我們假設為距離最小平方和（SSR）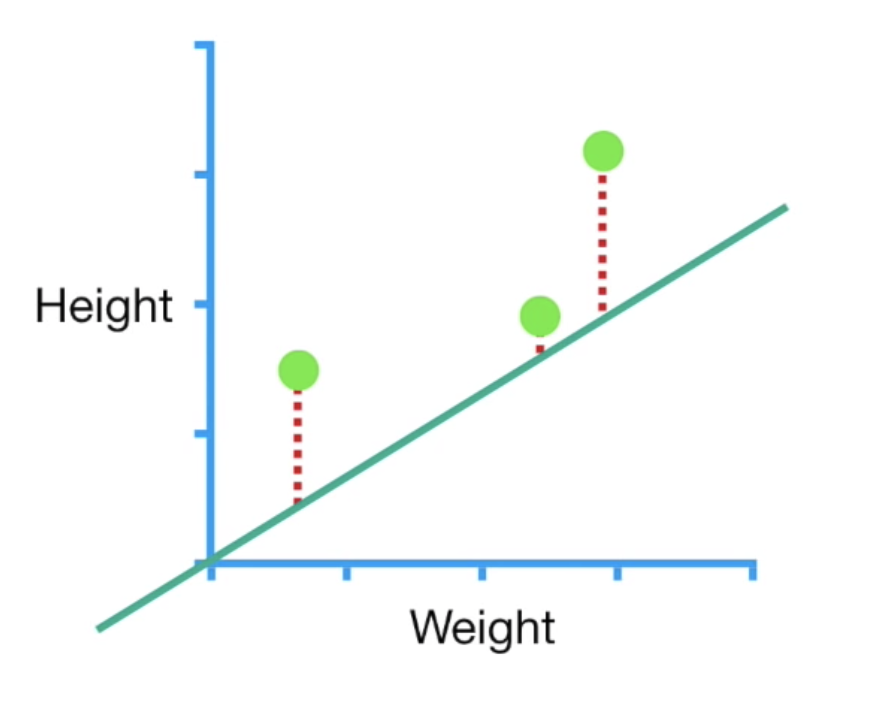

接下來我們幫b設置一個隨機起始值，計算SSR，根據起始值的不同，我們可以算出不同的SSR然後畫成如下右圖：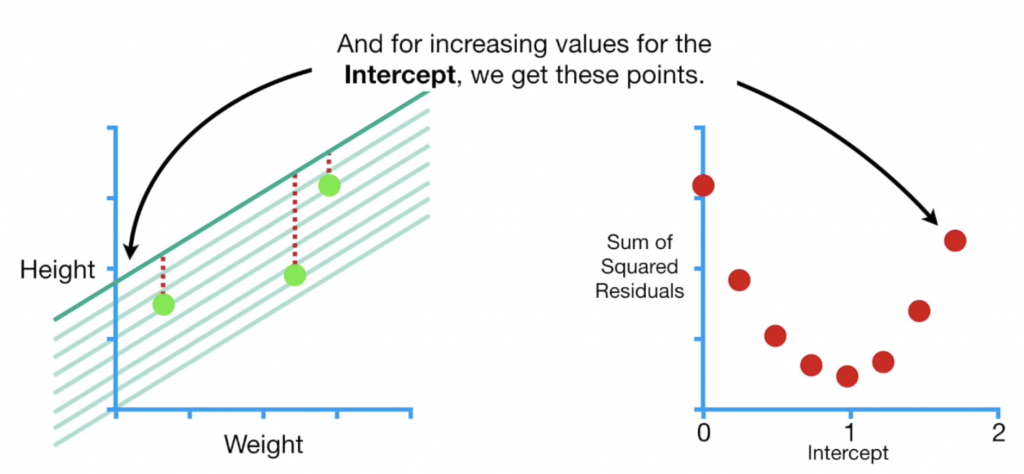

其實我們最想要找到的點就是右邊這個紅色曲線的最低點，也就是找到一個b值讓loss（SSR）最小，也就是曲線切線斜率等於0的位置。

偏微分就是讓你的b值從起始走到那個最理想的點的方式，首先按照步驟一，我們把所有資料帶入loss function之後對b做偏微：

data: (0.5, 1.4),(2.3, 1.9),(2.9, 3.2)
SSR = (y - y_pred)^2 =
(1.4 - (0.64 * 0.5 + b))^2 +
(1.9 - (0.64 * 2.3 + b))^2 +
(3.2 - (0.64 * 2.9 + b))^2
= (1.08 - b)^2 + (0.42-b)^2 + (1.34-b)^2

對b微分:
= 2(1.08 - b)(-1) + 2(0.42 - b)(-1)+2(1.34 - b)*(-1)
= -2(1.08 - b + 0.42 - b + 1.34 - b) **
= -5.68 + 3b

得到偏微結果後，我們就可以進入步驟二：對參數隨機設置起始值，我們假設b起始為0，所以帶入偏微結果等於-5.68，我們知道偏微就是斜率的概念，所以這個-5.68其實就是下圖紅色線的斜率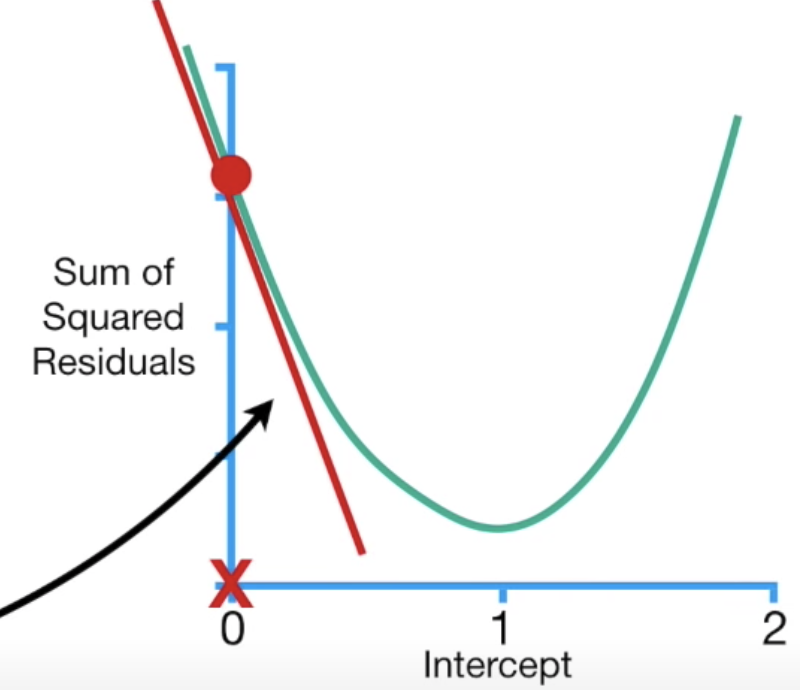

下一步驟是計算step，step=slope * learning rate，learning rate會影響到步伐的大小，如果走太小就會走很慢，如果走太大步可能就會直接錯過我們想找的loss最小值，這裏我們先設定為0.1，所以第一個step是-5.68 * 0.1 = -0.568，而下一個步驟是計算新的參數值：等於舊的參數值-step，也就是前一個b值-step = 0-(-0.568) = 0.568，根據計算的結果，我們往右走0.568的步伐，如下圖：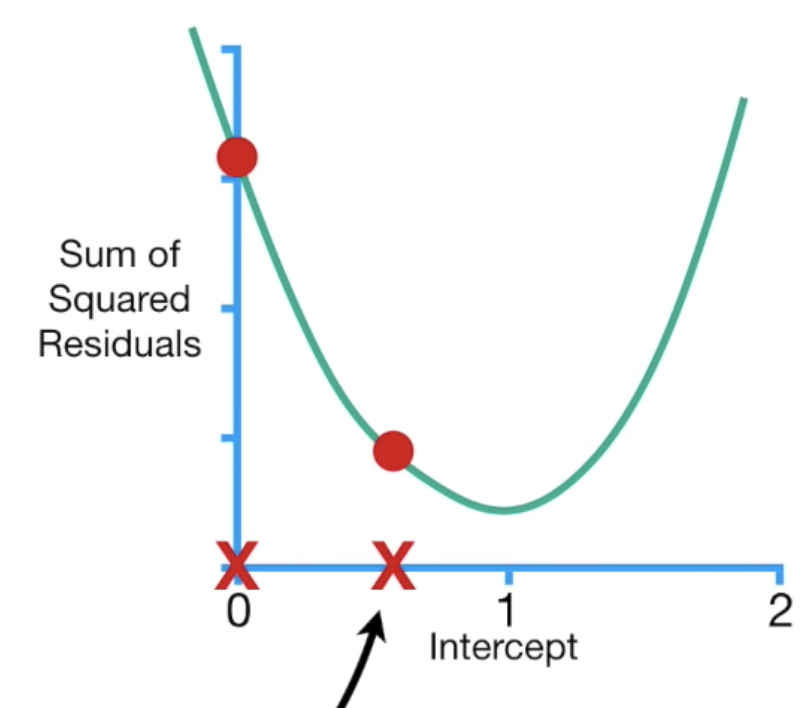

接下來就是重複的步驟，把新的b值帶回偏微公式（-5.68 + 3 * 0.568），然後計算新的step(0.568-(-0.397)=0.965)，依此類推，走到step趨近於0，就大功告成啦～

希望這篇文章可以讓大家更了解Gradient Descent的計算過程，其實並不複雜呦！

reference:
https://www.youtube.com/watch?v=sDv4f4s2SB8&t=653s