從上篇的confusion matrix可以延生出不同的比例，從比例我們也可以在延伸出不同的曲線來比較模型。

ROC curve

我們都知道logistic model基本上就是把linear model放進sigmoid function轉換成機率，但如果要回答分類問題（有心臟病/沒有心臟病），我們就需要設定threshold來判斷：假設threshold設定為0.5，那模型預測機率0.5以上的人模型都會說有心臟病，反之則沒有，我們可以藉由這個結果來產出一個confusion matrix，所以，不同的threshold就會產生不同的confusion matrix，我們可以計算出相應的比率來畫出ROC curve。

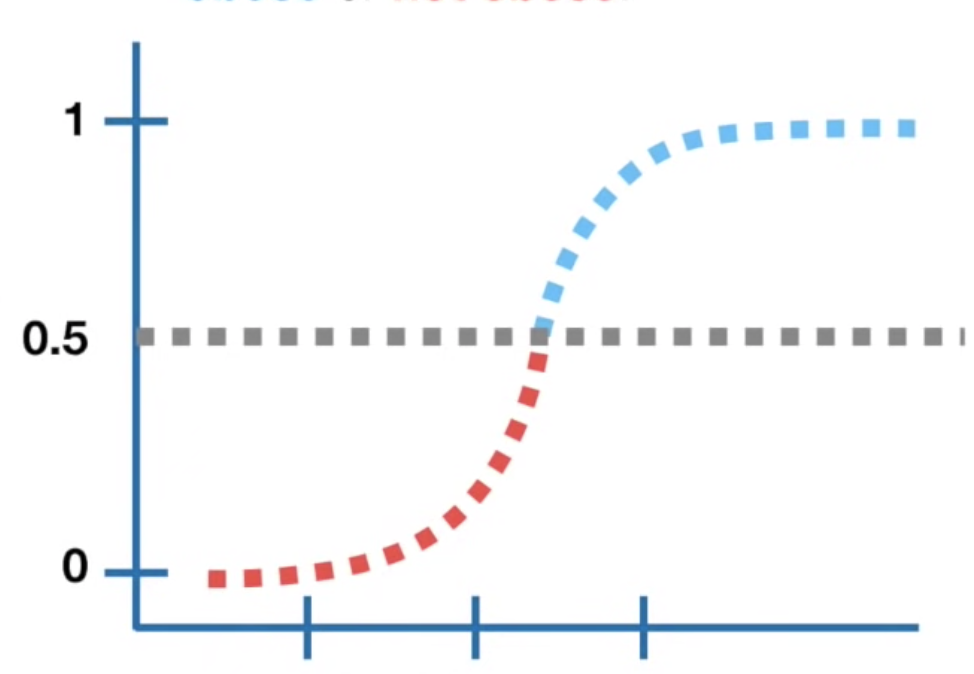
ROC curve其實就是統整不同confusion matrix結果的圖，y軸為sensitivity(true positive rate)，x軸為false positive rate (1-specificity)，透過同一個模型裡設定不同的threshold，我們可以畫出下圖：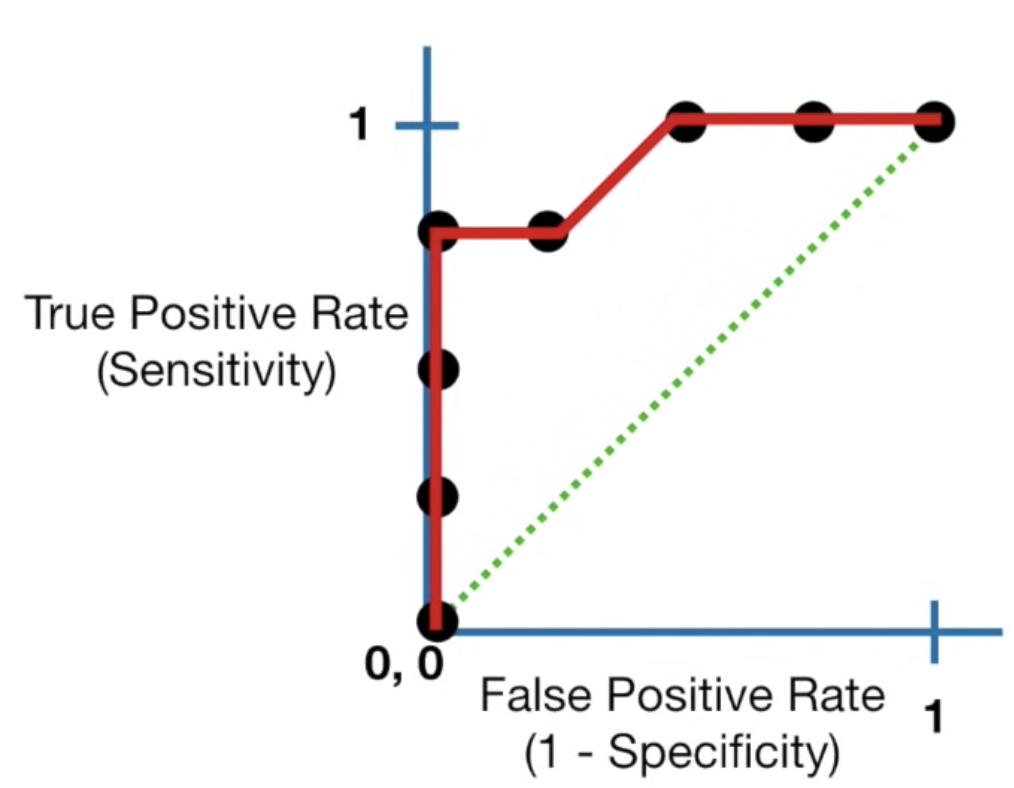

我們所希望的是true positive rate越高而false positive rate越低，所以最佳的threshold位置為靠近（0,1)的地方

AUC

那如果我們想要比較不同模型怎麼辦呢？因為每個模型都可以畫出自己的ROC curve，所以在比較不同模型時，我們可以計算AUC(area under the curve)：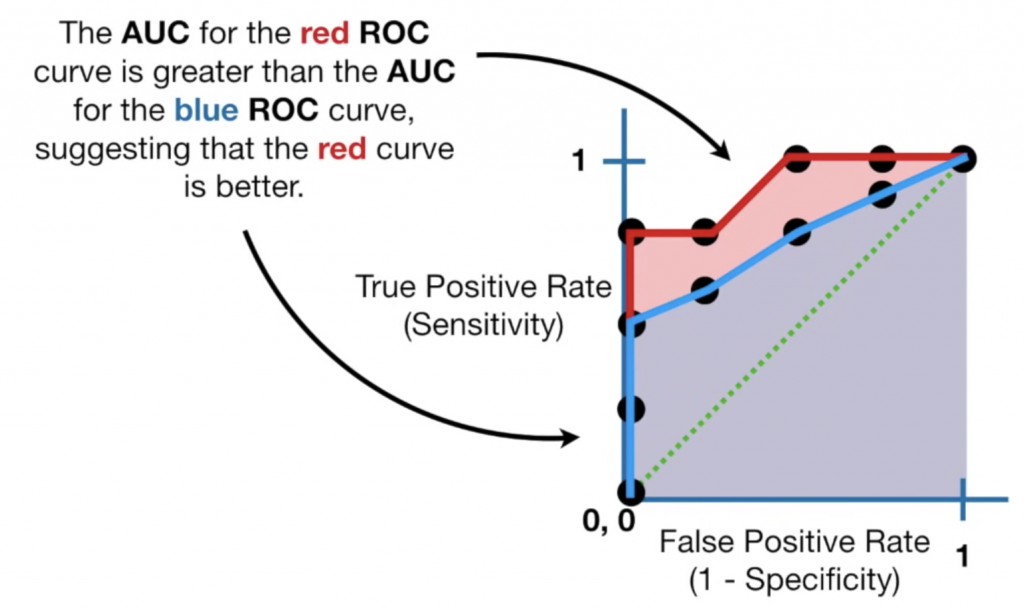

因為知道最佳的點會集中在（0,1)的區域，所以線下的面積越大，代表模型的表現越好，像是上圖就表示紅色線模型優於藍色線模型，我們對AUC數值的解讀為：隨機抽取一個正樣本，正確判斷的機率，通常AUC的範圍為：
AUC = 0.5: no discrimination
0.7 <= AUC <= 0.8: acceptable
0.8 <= AUC <= 0.9: excellent
0.9 <= AUC <= 1.0: outstanding

另外小小補充，因為ROC curve同時考量正例與負例，所以在負例多（不平衡）的資料中會表現得過度樂觀（TN多導致false positive rate 低），這時候我們會把x軸從false positive rate換成precision rate (TP/TP+FP)只專注於正例，此時曲線越靠近（1,1)越好，曲線稱為PR curve (precision-recall curve)。

reference:
https://www.youtube.com/watch?v=4jRBRDbJemM