昨天發完文後,覺得對於演算法還是心有不甘,便上網搜尋了一下,雖然沒直接給到答案,間接的給了我一些大膽的想法。
具體參考的是這篇:
https://ithelp.ithome.com.tw/articles/10231115
而當下的我了一個很草率的結論:迭代的效能比遞迴好
在樹的開篇有提到使用遞迴的原因是一般的迴圈做不出樹狀結構,但是效能上卻有瓶頸,接著我就意識到,先前的作法根本是「為了遞迴而遞迴」,我們只是需要透過樹狀結構來指定父子關係,那為什麼每次更新(渲染繪圖)的時候都還要跑遞迴呢?
因此我的思路是,把需要遞迴的放在建構式裡面,其他則透過跑迴圈的方式,於是,簡化了一開始的流程,分別只對樹根Tree進行定位,對於樹枝Stick只提供長度跟角度,接著在這個過程中把樹狀圖給扁平化,把眾樹枝們放到treeNodes裡面。
let treeNodes = [];
let Tree = function(x, y, r, theta, times){
treeNodes = [this];
this.startX = x;
this.startY = y;
this.endX = x + r * Math.cos(theta / 180 * Math.PI);
this.endY = y + r * Math.sin(theta / 180 * Math.PI);
this.r = r;
this.theta = theta;
this.grow = 0;
let shrink = 0.65 + random(0.1);
let diff = random(0.3) - 0.15; // +-0.15
this.son = [new Stick(this, (shrink - diff), 30 * (a+b+1), times - 1),
new Stick(this, (shrink + diff), 30 * (a-b-1), times - 1)];
}
let Stick = function(father, shrink_diff, angleOffset, times){
this.father = father;
this.r = this.father.r * (shrink_diff);
this.theta = this.father.theta + angleOffset;
this.grow = 0;
treeNodes.push(this);
if(times > 0){
let shrink = 0.65 + random(0.1);
let diff = random(0.3) - 0.15; // +-0.15
this.son = [new Stick(this, (shrink - diff), 30 * (a+b+1), times - 1),
new Stick(this, (shrink + diff), 30 * (a-b-1), times - 1)];
}
}
於是,在物件實例化的過程中,我們就拿到了treeNodes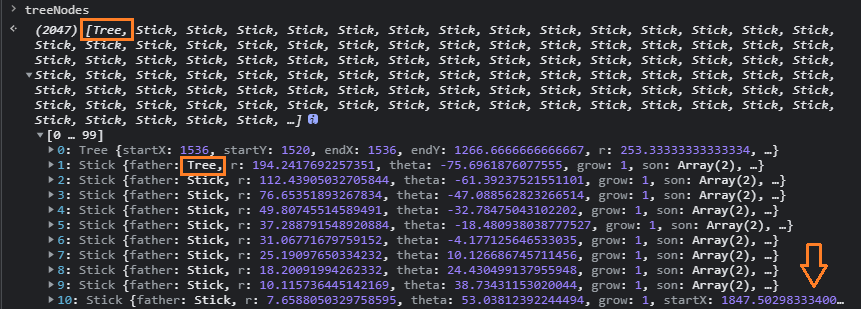
裡面有三處標記,說明一下:
- treeNodes[0]是一開始放進去的Tree物件
- Tree有兩節子樹枝,其中一枝和它後面2^9的子子孫孫都會排序其後
- 右下角顯示該樹枝沒有子代,表示到treeNodes[10]實際上已經遞迴10次
然後就可以把每一偵都要跑的,原本遞迴寫法Transform和Draw通通改成for迴圈,這邊和之前主要的差異在於,之前要用this,現在用node = treeNodes[N],和判斷樹枝在左側或右側。
Tree.prototype.Transform = function(){
let a = myMouse.pointX;
let b = myMouse.pointY;
for(let N = 1; N < treeNodes.length; N++){
let node = treeNodes[N];
let index = node.father.son.indexOf(node);
let parameter = ((index == 0)?(a+b+1):(a-b-1));
// if(index == 0) console.log(0);
// else console.log(1);
node.theta = node.father.theta + 30 * parameter;
// 已知father, r, theta 三個參數,透過father取得座標後進行計算
let x = node.father.endX;
let y = node.father.endY;
let r = node.r;
let theta = node.theta;
node.startX = x;
node.startY = y;
node.endX = x + r * Math.cos(theta / 180 * Math.PI);
node.endY = y + r * Math.sin(theta / 180 * Math.PI);
}
};
Tree.prototype.Draw = function(){
for(let N = 1; N < treeNodes.length; N++){
let node = treeNodes[N];
let x = (node.startX - WIDTH/2) * node.grow + WIDTH/2,
y = (node.startY - HEIGHT)* node.grow + HEIGHT,
r = node.r * node.grow,
theta = node.theta;
context.beginPath();
context.moveTo(x, y);
context.lineTo(x + r * Math.cos(theta / 180 * Math.PI),
y + r * Math.sin(theta / 180 * Math.PI));
context.lineWidth = 1 + r/50;
context.strokeStyle = 'rgba(179, 198, 213, 1)';
context.stroke();
node.grow = Math.min(node.grow + 0.01 / (0.8 + 2 * node.grow), 1);
}
};
值得一提的是父子之間一定有前後順序,不一定相鄰,但是父樹枝一定在陣列比較前面的地方,因此不必擔心父樹枝的座標未經演算,就被子樹枝拿去作使用,這也是扁平化的時候就要先設計好的。
稍作體感上有感受到很微妙的差異,CPU則同樣在50%~80%之間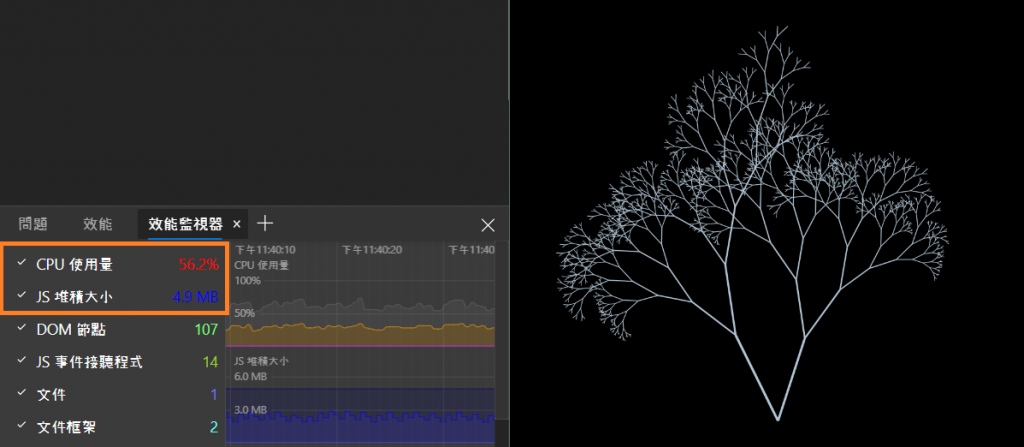
(五年老筆電i7-6700)
後來再回去拜讀了一下開頭貼的文章,發現它談論的只是如何讓遞迴的Stack不要爆炸(記憶體超過最大限制),所以嚴格來說雖然有優化,因為不會占用記憶體空間,不過運算樹的座標本身還是需要演算的時間,要求1秒60偵,也就是每16豪秒計算一次,算是要求相當高,對CPU的負荷仍不會少。
同樣以prototype的寫法來執行一次完整的動畫:
不過原本的是在github.io上做測試,今天的在本地端做測試,可能會有些許誤差
我對資料結構還不夠熟悉,等系列文結束之後再來慢慢研究迭代跟遞迴吧!
不過針對演算的時間,我們理論上應該還是可以透過減少浮點數的運算,來讓程式效率更佳,到時候該做的還是逃不掉!
結果又沒時間美化樹枝了XDD,本著程式越複雜之後越難改的心情,先跑回來重寫遞迴,果然還是沒那麼容易呢!而且今天白天跑去爬柴山了,回來整個動彈不得Ww,差點沒睡死在床上,原本也想仔細解釋上面程式碼在寫什麼,不過時間不太夠了,如果有需要的話,留言跟我說,再補充。
