前言：相信大家對於「樹」都不陌生，資料結構中的樹其實是模擬現實生活中的樹幹、樹枝和葉子，相當於樹狀結構的資料集，這時的資料已經不像之前的陣列、鏈結串列一樣是線性的資料結構，而是階層性的非線性資料結構。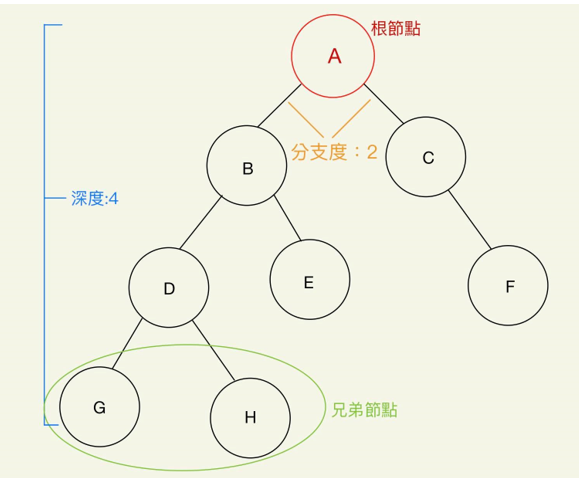

名詞介紹：

• 根節點或樹根(Root)：位於樹狀結構的最頂端，上方沒有其他節點。例如：A

• 父節點(Parent)、子節點(Children)：若A節點的下方還有B節點，則就可稱A節點為B節點的父節點；反之，B節點為A節點的子節點。

• 葉節點(Leaf)：沒有子節點的節點稱為葉節點。例如：G、H、E、F

• 祖先節點(Ancenstors)：指某節點到跟節點之間所經過的所有節點。例如：G的祖先節點為D、B

• 非終端節點(Noterminal)：除了葉節點之外的其他節點，都可稱為非終端節點。例如：A、B、C、D

• 兄弟節點(Siblings)：指有共同的父節點。例如：G和H為兄弟節點

• 分支度(Degree)：指每個節點所擁有的子節點樹。例如A的分支度為2

• 階層(Level)：若樹根是一，其子節點是二，則可依序推算出樹的階層樹。例如：A的階層是一，B、C的階層是二，以此類推。

• 樹深(Depth)：又稱為樹高(Height)，指樹的最大階層數。

• 子樹(Subtree)：每一個子集合也是一棵樹，而這些樹稱為根節點的子樹。

樹的定義：樹的節點個數是一或多個有限集合，必存在一個根節點且各節點之間不能有迴圈產生或不連結的子樹。

二元樹(Binary Tree)：

二元樹的定義：二元樹為資料結構中最廣泛運用的樹狀結構，其特點為樹中的每個節點最多只能有兩個子節點(分支度<=2)。二元樹的節點個數是一個有限集合，或是沒有節點的空集合。二元樹的節點可以分成兩個沒有交集的子樹，稱為「左子樹」（Left Subtree）和「右子樹」（Right Subtree）。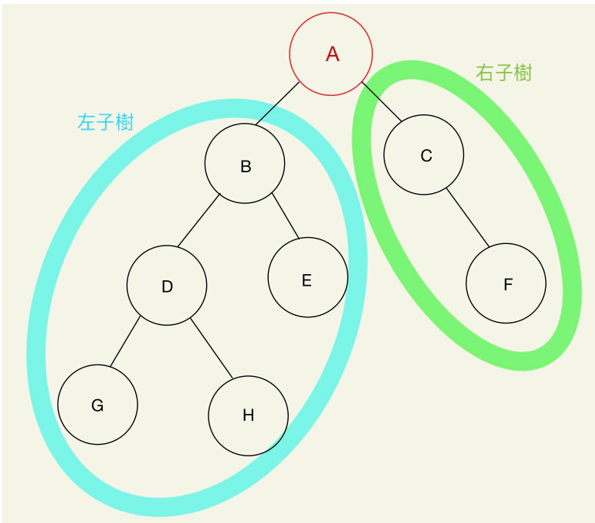

歪斜樹（Skewed Tree）：當一顆樹只有左邊節點或右邊節點時，就可以稱做歪斜樹。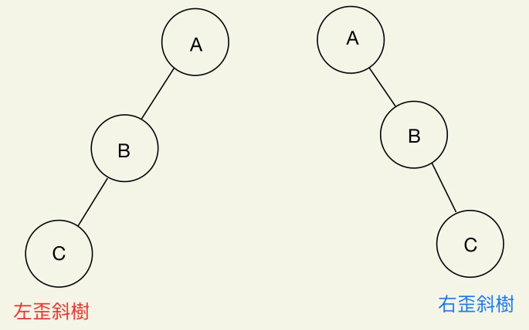

完滿二元樹（Full Binary Tree）：如果二元樹的樹高是h且二元樹的節點數是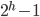 ，滿足此條件的樹則可稱為完滿二元樹。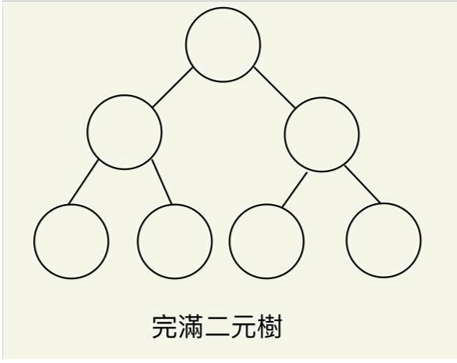

完整二元樹(Complete binary tree)：如果二元樹的深度為h，所含的節點數小於 ，但其節點的編號方式如同深度為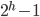的完滿二元樹一般，從左到右，由上到下的順序一一對應結合，則可稱為完整二元樹。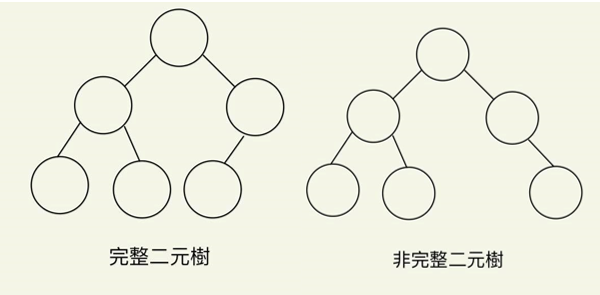

嚴格二元樹：二元樹的每個非終端節點均有非空的左右子樹，則可稱為嚴格二元樹。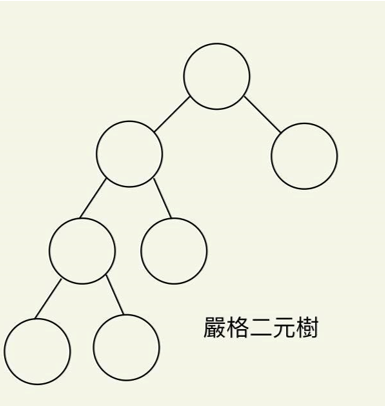

本日小結：今天介紹了樹狀結構和二元樹，這次雖然沒有實作但卻有大量的名詞解釋，先把樹狀結構的名詞記熟再學習二元樹會比較輕鬆喔！二元樹雖然很多中類很複雜，但本質上就算是一種二分法，在生活中我們常常面臨許多選擇，當決策的方式越來越少，事情也就看似簡單了一點，明天就要開始實作二元樹的處存方式o(^∀^*)o