前言：上一篇介紹過了樹狀結構和二元樹，今天要來介紹二元樹存取資料的方法，其中有兩種方法最常使用，這次都會帶大家好好了解。

陣列表示法：

利用陣列結構儲存資料的二元樹，節點編號具有循序性，一此方法可得到節點編號的規則，例如：左節點編號是父節點編號乘以2；右節點編號是父節點編號乘以2+1。

建立規則：
•將陣列的第1個元素插入二元樹成為根節點。

•將陣列元素值與二元樹的節點值做比較，如果元素值大於節點值，將元素值插入成為節點的右子節點，如果右子節點不是空的，重覆比較節點值，直到找到插入位置後，將元素值插入二元樹。

•如果元素值小於節點值，將元素值插入成為節點的左子節點，如果左子節點不是空的，繼續重覆比較，以便將元素值插入二元樹。

優點：適合用來存取完滿二元樹。因為陣列表示法的節點具有循序性，完滿二元樹的儲存能夠有效運用記憶體空間，避免造成不必要的浪費。

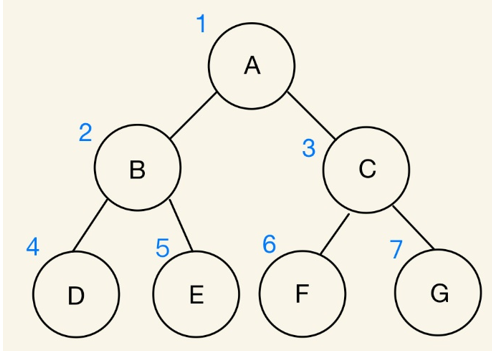
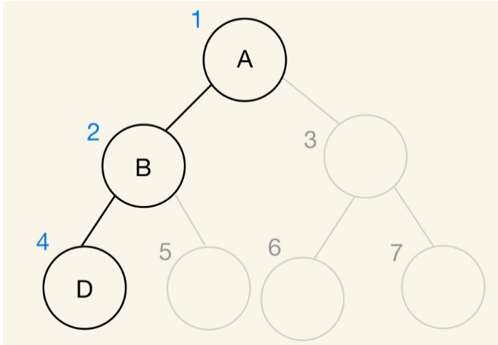
缺點：不適合用來存取歪斜樹。同樣因為節點的循序性，就算節點內沒有資料，陣列也不會刪除儲存子節點資料的記憶體，而是形成一個空集合，造成記憶體的浪費。

實作程式碼：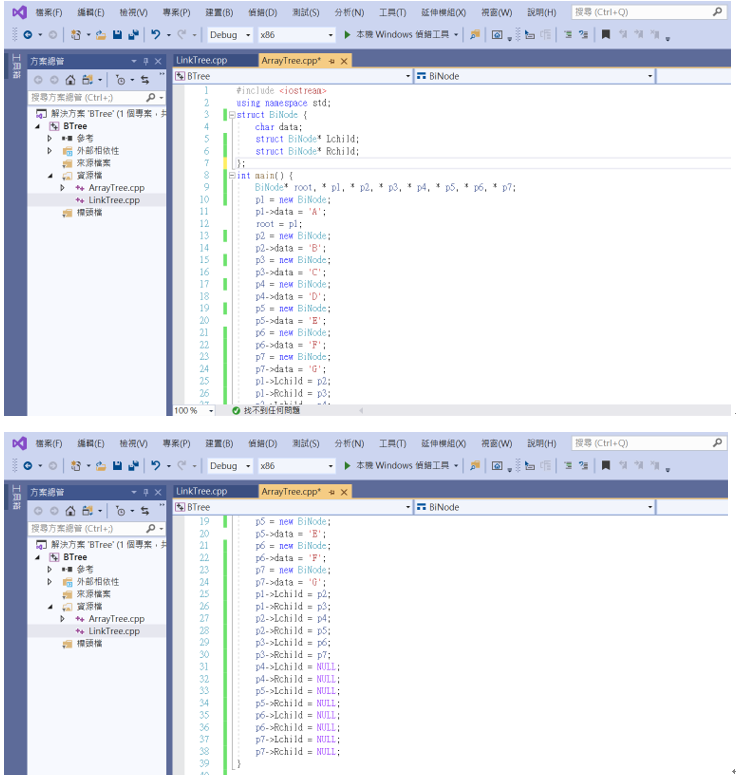

現在沒有執行結果是因為程式碼還沒有走訪的順序，所以執行了也沒有東西，這部分的內容明天就會討論到了喔！

鏈結串列表示法：

利用鏈結串列儲存資料的二元樹，每個節點中會多出兩個指向子節點的指標(一左一右)

優點：適合用來存取歪斜樹，鏈結串列表示法的二元樹只會將指標指向的資料儲存，所以並不會像陣列表示法一樣浪費過多的空間。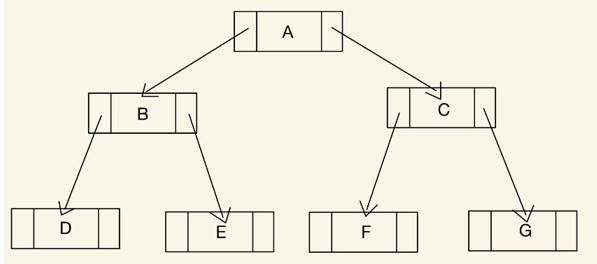

缺點：不適合用來存取完滿二元樹，需要多使用到記憶體空間儲存各節點的左右指標，會比起陣列表示法浪費空間。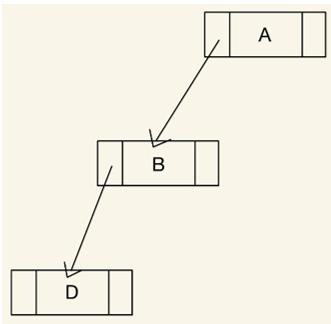

實作程式碼：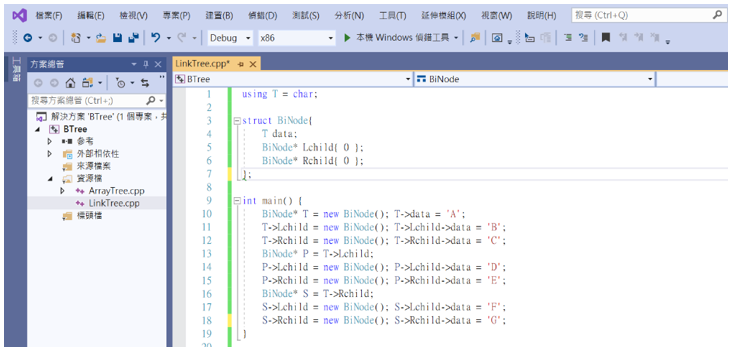

本日小結：今天介紹了二元樹的兩種儲存方式，明天就要照著這個程式碼實作二元樹的走訪，這也是相當重要的環節，不同的走訪方式就會有不同的結果，怎麼樣的走訪方式適合在甚麼地方使用將會是明天的重點o(-д´- ｡)

陣列表示法

#include <iostream>
using namespace std;
struct BiNode {
	char data;
	struct BiNode* Lchild;
	struct BiNode* Rchild;
};

int main() {
	BiNode* root, * p1, * p2, * p3, * p4, * p5, * p6, * p7;
	p1 = new BiNode;
	p1->data = 'A';
	root = p1;
	p2 = new BiNode;
	p2->data = 'B';
	p3 = new BiNode;
	p3->data = 'C';
	p4 = new BiNode;
	p4->data = 'D';
	p5 = new BiNode;
	p5->data = 'E';
	p6 = new BiNode;
	p6->data = 'F';
	p7 = new BiNode;
	p7->data = 'G';
	p1->Lchild = p2;
	p1->Rchild = p3;
	p2->Lchild = p4;
	p2->Rchild = p5;
	p3->Lchild = p6;
	p3->Rchild = p7;
	p4->Lchild = NULL;
	p4->Rchild = NULL;
	p5->Lchild = NULL;
	p5->Rchild = NULL;
	p6->Lchild = NULL;
	p6->Rchild = NULL;
	p7->Lchild = NULL;
	p7->Rchild = NULL;
}

鏈結串列表示法

using T = char;

struct BiNode {
	T data;
	BiNode* Lchild{ 0 };
    BiNode* Rchild{ 0 };
};

int main() {
BiNode* T=new BiNode(); T->data= 'A';
T->Lchild=new BiNode(); T->Lchild->data= 'B';
T->Rchild=new BiNode(); T->Rchild->data= 'C';
BiNode* P=T->Lchild;
P->Lchild=new BiNode(); P->Lchild->data= 'D';
P->Rchild=new BiNode(); P->Rchild->data= 'E';
BiNode* S=T->Rchild;
S->Lchild=new BiNode(); S->Lchild->data= 'F';
S->Rchild=new BiNode(); S->Rchild->data= 'G';
}