圖(Graph)，並非多數人直接聯想到形狀或圖片，在計算機科學或離散數學中的圖，是由數個頂點Vertex(或稱節點Node)及數條邊(Edge)所構成，頂點與頂點之間用邊連接，用來表示兩點的關聯與關係。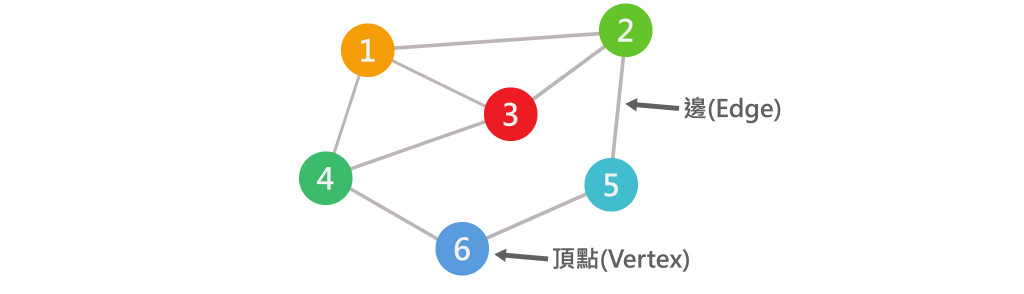

一個圖可以用G=( V, E )來定義

• G： 圖形(Graph)
• V： 所有頂點(Vertice)的集合
• E： 所有邊(Edges)的集合

同構(Isomorphism)

同構是指若兩個以上的圖，它們頂點與頂點之間的關聯是一致的，就是同構的圖。

上方圖，無論直線或曲線，只要頂點間的關聯一樣，就屬於同構圖。

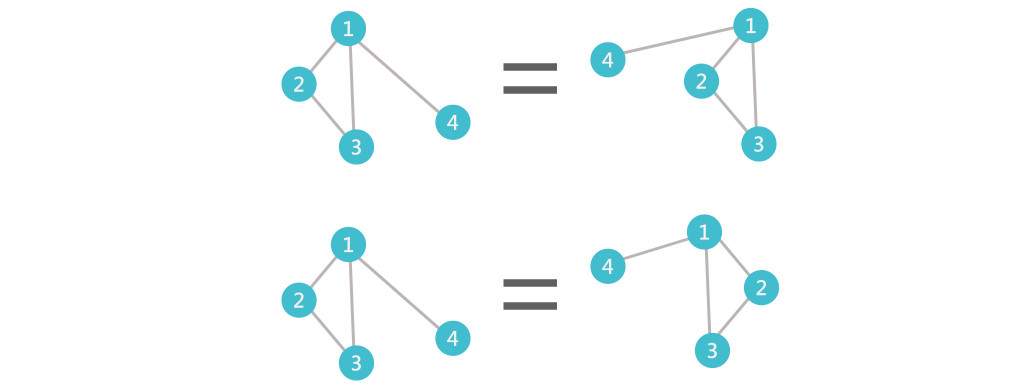
上方圖，頂點位置被任意移動，只要頂點間的關聯一樣，就屬於同構圖。

有向圖(Directed Graph)

具有方向性的邊，表示某個邊是單向的。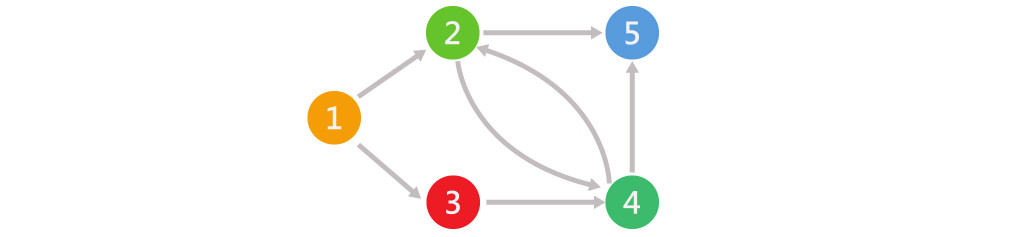

無向圖(Undirected Graph)

不具有方向性的邊，表示某個邊是雙向的。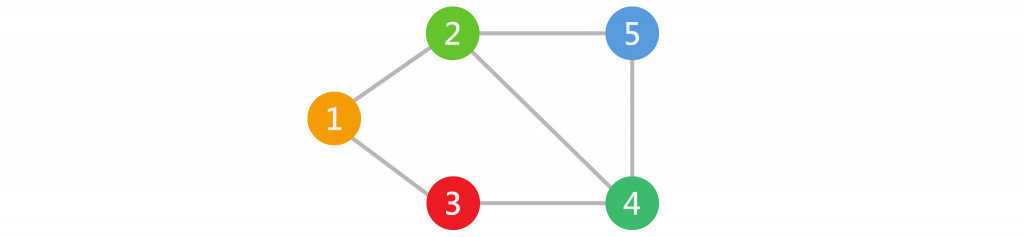

加權圖(Weighted Graph)

邊上附有數值稱為邊的「加權」或 「權重」，可以表示出相聯的兩頂點的連接程度，常見的權值應用有: 成本、距離、時間……等。
可以想像台北捷運圖，各站即為頂點，站與站之間的路線就是邊，各站間會有票價權重;Google地圖，兩景點間路徑計算，會有距離的權重;社交軟體的關係鏈中，誰與誰的共同好友數可以為權重，又或是各伺服器間通訊的時間。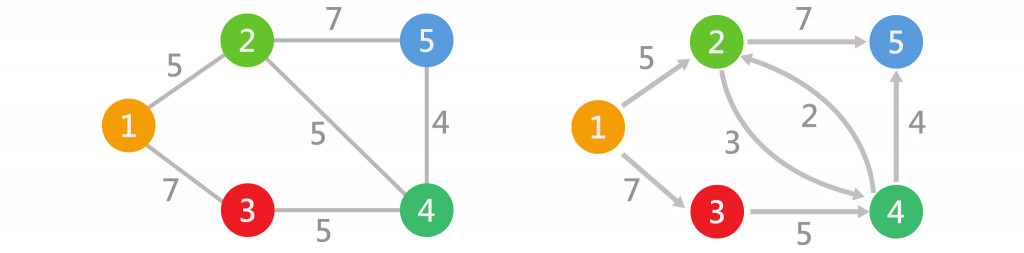

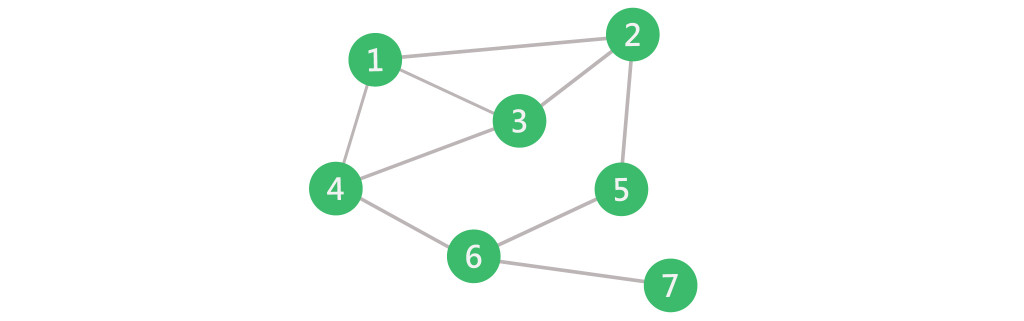
圖的術語

• 路徑(Path)：兩頂點經過的邊。如上圖:1到6，可以從1到4再到6，可以說(1,4,6)為其路徑。
• 路徑長度(Path Length)：兩頂點路徑上包含邊的個數。如上圖:1到6，路徑為 {(1,4), (4,6)}，經過２條邊。
• 簡單路徑(Simple Path)：路徑上除了起點與終點可以相同外，其餘頂點不能被重複經過。如上圖:
  1 4 6為簡單路徑，頂點都未重複。
  1 4 3 2 1為簡單路徑，1為起終點，其餘頂點都未重複。
  2 3 4 1 3 2不為簡單路徑，其中的頂點3出現2次。
• 循環(Cycle)：屬於簡單路徑，且路徑的起點與終點相同能構成循環。如上圖:3 2 1 4 3，起點與終點都是3。
• 相鄰(Adjacent)：兩個頂點間有一條邊相連(不論是否具有方向性)，則這兩個頂點為相鄰。如上圖:3與1 2 4相鄰。
• 分支度(Degree)：

  • 無向圖中: 一個頂點含有幾條邊，如下圖:B的分支度為2。
    

  • 有向圖中: 入分支度與出分支度的總和，如下圖B的分支度為3。

    • 入分支度(In-Degree)： 箭頭指入此頂點的邊數，如下圖B的入分支度為2。
    • 出分支度(Out-Degree)： 箭頭由此頂點指出的邊數，如下圖B的出分支度為1。
      
• 完整圖(Complete Graph)：
  • 無向圖中: n 個頂點，會有n(n-1) ÷ 2條邊，如下圖: 4個頂點，6條邊。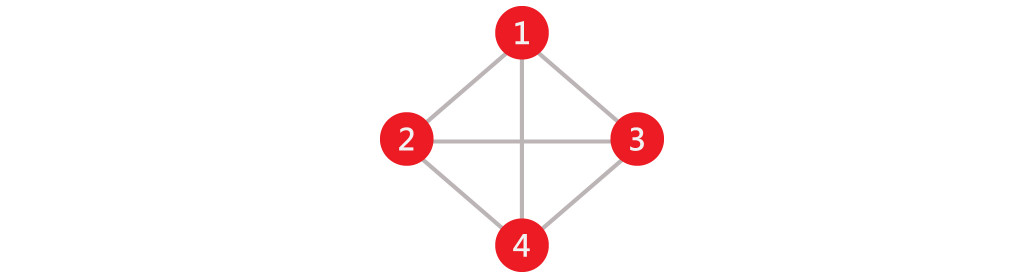
    
  • 有向圖中: n 個頂點，會有n(n-1)條邊，如下圖: 4個頂點，12條邊。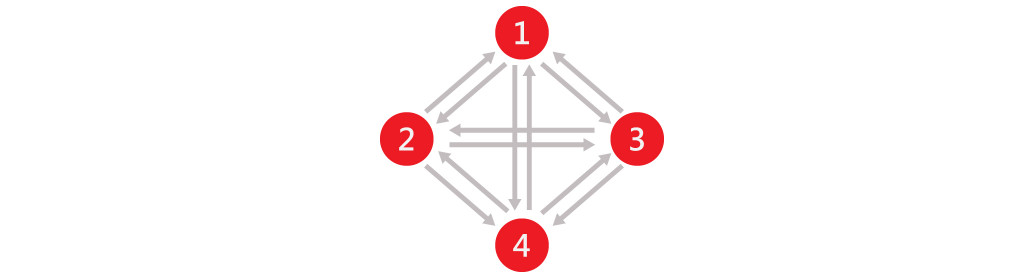
    
• 子圖(Subgraph)：如下圖:乙圖與丙圖的頂點被包含在甲圖的頂點集合中，且乙圖與丙圖的邊也被包含在甲圖的邊集合中，則可以說乙與丙是甲的子圖。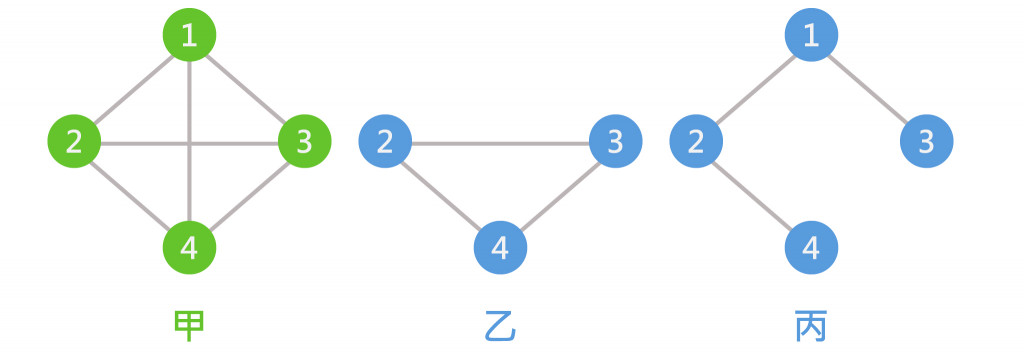
  

常見圖的表示法

相鄰矩陣 (Adjacency Matrix)

一個包含N個頂點的圖，可以使用 N 乘 N 的二維陣列來表示，兩個頂點間，若有邊值為1；若沒有邊值為0。

• 無向圖中:
  

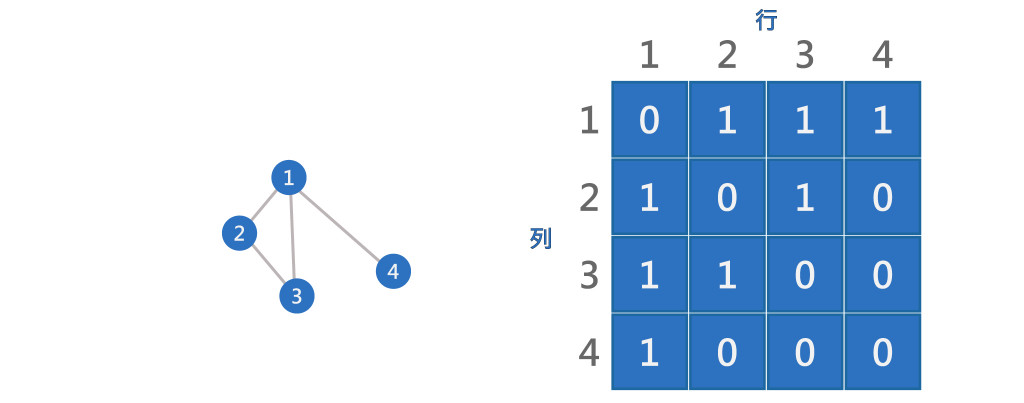
矩陣會是對稱的，如上圖G[2][3] = G[3][2] = 1，只需保存上三角或下三角部份即可，n(n-1)/2的記憶體空間。
分支度: 該頂點在矩陣中列的總和，如上圖：頂點2的分支度 = 1 + 0 + 1 + 0 = 2

• 有向圖中:
  

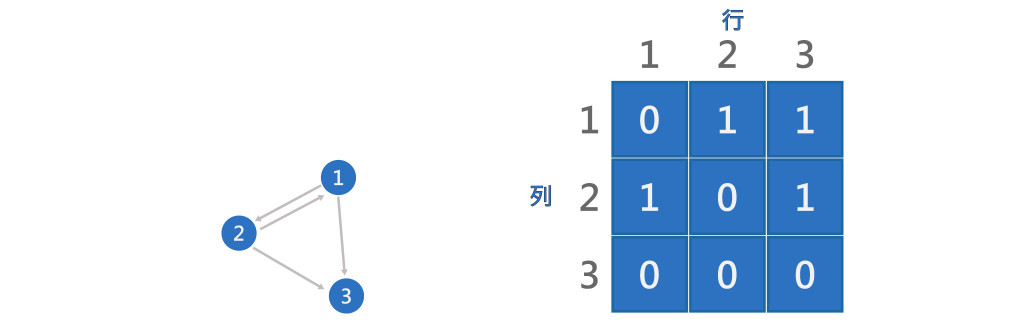
矩陣不一定會是對稱的，如上圖G[1][3]=1，G[3][1]=0。
分支度: 該頂點入分支度與出分支度的總和。
出分支度： 第i列的總和，如上圖的頂點3，出分支度為第3列的總和為 0。
入分支度： 第i行的總和，如上圖的頂點3，入分支度為第3行的總和 1 + 1 + 0 = 2

相鄰串列 (Adjacency List)

每個頂點使用單向鏈結串列來串接相鄰的頂點，只處理有邊的部分，沒有邊的部分不處理，有N個頂點，需準備N個串列，再用指標指向相鄰頂點。

• 無向圖中:
  

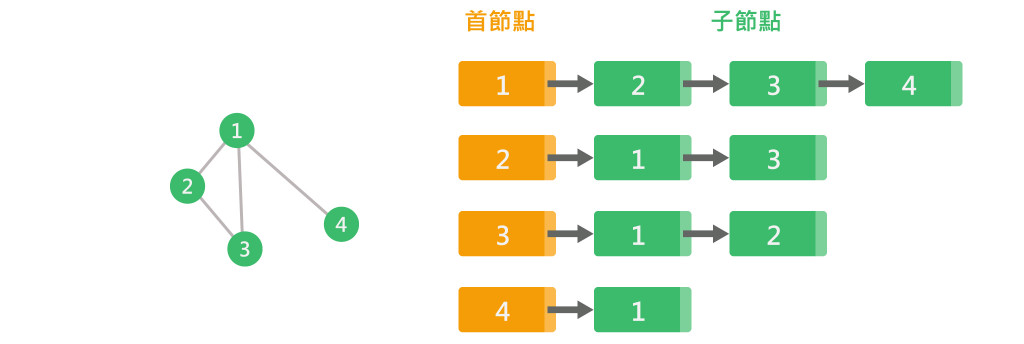
若有n個頂點，e條邊，則需要 n 個首節點與 2乘e 個子節點，如上圖有4個頂點，與4條邊，則需要4個首節點與8個子節點。
分支度: 該頂點串列子節點的總數，如上圖:頂點1的串列，除了首節點之外，有3個子節點，分支度為 3

• 有向圖中:
  

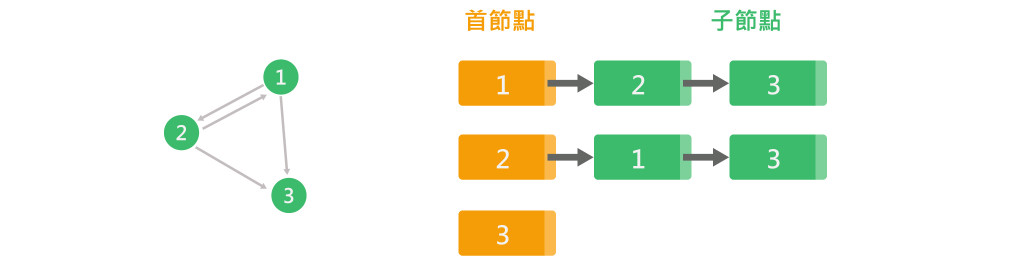
若有n個頂點，e條邊，則需要 n 個首節點與 e 個子節點，如上圖有3個頂點，與4條邊，則需要3個首節點與4個子節點。
出分支度： 該頂點串列子節點的總數，如上圖:頂點1的串列，除了首節點之外，有2個子節點，出分支度為 2。
入分支度： 比較複雜，需要尋找其他頂點串列的子節點，是否出現該頂點，再加總。

相鄰矩陣在路經很少的情況下容易浪費空間，但求分支度就非常方便，而相鄰串列法比較節省空間，但求分支度時比較麻煩。