前言：資料結構的部分已經到了尾聲，今天就要開始初探演算法的搜尋了！間天介紹的這兩個搜尋法都是始於入門款，現在就來看看吧！

搜尋的概念：

在數據集合中尋找滿足某種條件的數據元素。

平均搜尋長度(Average Search Length)
• 搜尋就是不斷將數據元素的關鍵字與待查找關鍵字進行比
較，搜尋法在成功時平均比較的次數稱作平均搜尋長度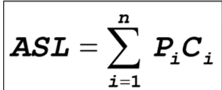

• Pi：搜尋第i個數據元素的機率
• Ci：搜尋該元素的過程中比較的次數

線性搜尋法：

又稱為循序搜尋法(Sequential Search)，這種演算法是最簡單的，從第一筆資料到最後一筆資料進行比對，直到找到想找的資料就行。舉個簡單的例子：在書店買書的時候，若不是像漫畫小說一樣有集數的話，是不是都要一本一本掃過去才能找到像要的書？

圖片來源：https://meet.eslite.com/Content/Images/Article/cats_20190214134118.jpg
這樣就是線性搜尋喔！只不過資料量少還可以，資料量多就越沒有效率了。

接著來實際實作看看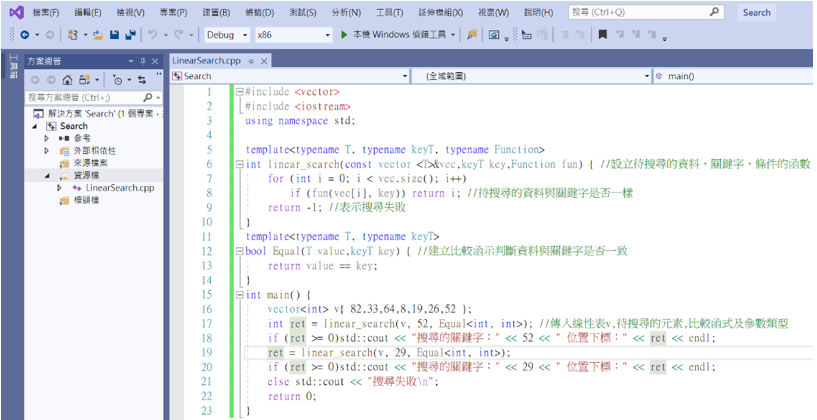

可以看到第一個搜尋的52有成功並標示出下標(82的下標為0)，而第二個搜尋的29則顯示失敗。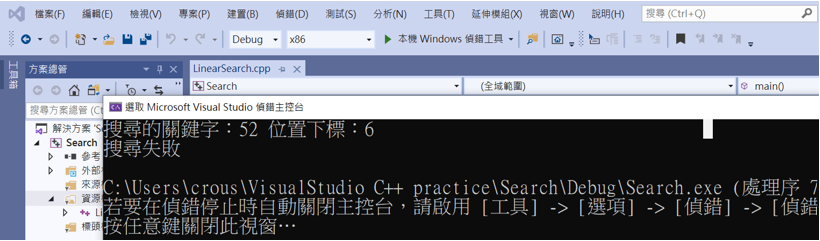

二分搜尋法：

又稱為二元搜尋法(Binary Search)，通常用在已經整理好(有序數組)的資料，會先把資料分成前半部和後半部，如果想要找的資料在前半部，則在把前半部分分成兩半，直到找到資料為止，這種搜尋法適合用在沒有增刪的靜態資料。
P.S.如果資料量為基數，則會無條件進位。

實際時做看看就明白怎麼操作的了。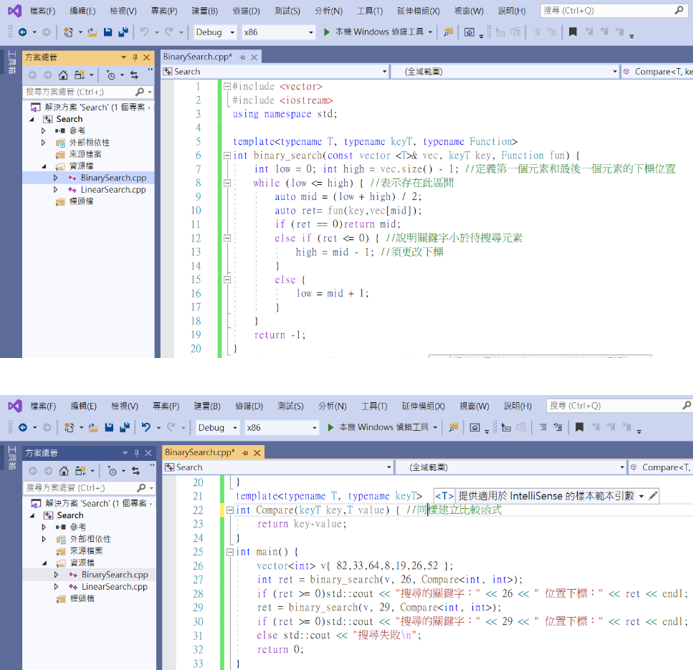

同樣可以輸出結果。

接著來比較看看兩個搜尋法查找的次數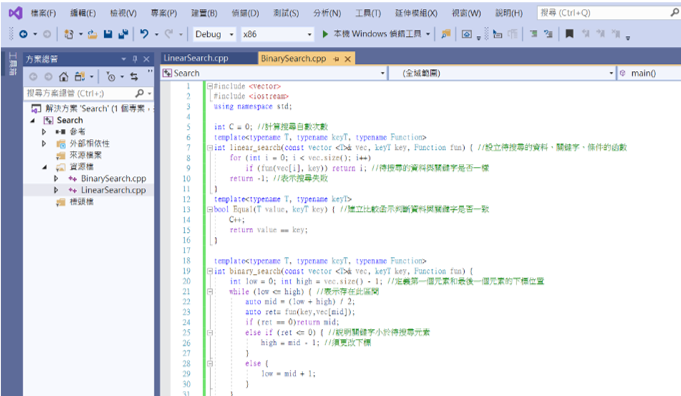


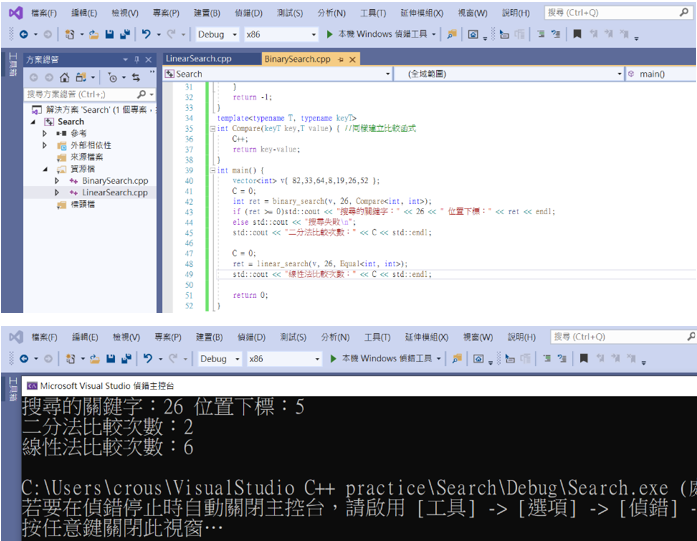
這樣就明顯的必較出瞭著的差異了。

最後再來分析兩個演算法的時間複雜度。(描述演算法的執行時間，時間複雜度越低代表效率越好) P.S.假設資料皆為n筆。

線性搜尋法：
	最壞情況：找到最後一筆才找資料，時間複雜度為O(n)。

    最好情況：第一筆剛好就是想找的資料，時間複雜度為O(1)。
    
二元搜尋法：
	最壞情況：每次找資料都切半，需要網前半部或後半部找，時間複雜度為O(log n)。

    最好情況：第一次切半的中間值剛好就是想找的資料，時間資料的複雜度為O(1)。

本日小結：今天介紹完了兩個基本的搜尋法，其他還有內插和費式同樣也是常見的搜尋法，不過礙於篇幅可能無法介紹到，有興趣的人可以到網路上找找相關資料，幾乎都有很詳細的解說喔o(^∀^)o

線性搜尋法

#include <vector>
#include <iostream>
using namespace std;

template<typename T, typename keyT, typename Function>
int linear_search(const vector <T>&vec,keyT key,Function fun) { //設立待搜尋的資料、關鍵字、條件的函數
	for (int i = 0; i < vec.size(); i++)
		if (fun(vec[i], key)) return i; //待搜尋的資料與關鍵字是否一樣
	return -1; //表示搜尋失敗
}
template<typename T, typename keyT>
bool Equal(T value,keyT key) { //建立比較函示判斷資料與關鍵字是否一致
	return value == key;
}

int main() {
	vector<int> v{ 82,33,64,8,19,26,52 }; 
	int ret = linear_search(v, 52, Equal<int, int>); //傳入線性表v,待搜尋的元素,比較函式及參數類型
	if (ret >= 0)std::cout << "搜尋的關鍵字：" << 52 << " 位置下標：" << ret << endl;
	ret = linear_search(v, 29, Equal<int, int>);
	if (ret >= 0)std::cout << "搜尋的關鍵字：" << 29 << " 位置下標：" << ret << endl;
	else std::cout << "搜尋失敗\n";
	return 0;
}

二元搜尋法

#include <vector>
#include <iostream>
using namespace std;

int C = 0; //計算搜尋自數次數
template<typename T, typename keyT, typename Function>
int linear_search(const vector <T>& vec, keyT key, Function fun) { //設立待搜尋的資料、關鍵字、條件的函數
	for (int i = 0; i < vec.size(); i++)
		if (fun(vec[i], key)) return i; //待搜尋的資料與關鍵字是否一樣
	return -1; //表示搜尋失敗
}
template<typename T, typename keyT>
bool Equal(T value, keyT key) { //建立比較函示判斷資料與關鍵字是否一致
	C++;
	return value == key;
}

template<typename T, typename keyT, typename Function>
int binary_search(const vector <T>& vec, keyT key, Function fun) {
	int low = 0; int high = vec.size() - 1; //定義第一個元素和最後一個元素的下標位置
	while (low <= high) { //表示存在此區間
		auto mid = (low + high) / 2;
		auto ret= fun(key,vec[mid]);
		if (ret == 0)return mid;
		else if (ret <= 0) { //說明關鍵字小於待搜尋元素
			high = mid - 1; //須更改下標
		}
		else {
			low = mid + 1;
		}
	}
	return -1;
}
template<typename T, typename keyT>
int Compare(keyT key,T value) { //同樣建立比較函式
	C++;
	return key-value;
}
int main() {
	vector<int> v{ 82,33,64,8,19,26,52 };
	C = 0;
	int ret = binary_search(v, 26, Compare<int, int>); 
	if (ret >= 0)std::cout << "搜尋的關鍵字：" << 26 << " 位置下標：" << ret << endl;
	else std::cout << "搜尋失敗\n";
	std::cout << "二分法比較次數：" << C << std::endl;

	C = 0;
	ret = linear_search(v, 26, Equal<int, int>);
	std::cout << "線性法比較次數：" << C << std::endl;
	
	return 0;
}