前言：昨天先燒為帶大家認識最簡單的搜尋類型，今天要來介紹之前有稍微提到的二元搜尋樹，並實作給大家看看。

二元搜尋樹：

又可稱為有序二元樹（ordered binary tree）或排序二元樹（sorted binary tree），先來講講二元搜尋樹的定義。
屬於二元樹的一種，如果任意的節點的左右子樹都不為空的話，則左子樹節點的值<根節點的值<右子樹節點的值，任意節點的左右子樹也都為二元搜尋樹，但不允許存在關鍵字相同的兩個節點。
通常使用鏈結串列當作二元搜尋樹的儲存結構。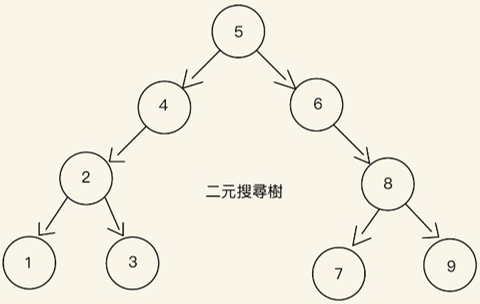

如何用二元搜尋樹進行查找？其實非常簡單，因為右子節點的值一定大於左子節點的值，所以一開始只要從跟節點比較，就可以知道要往左子樹還是柚子樹前進，再與其他子節點比較，就能找出最後所要找的值。

AVL Tree(Adelson-Velsky and Landis Tree)：

中文稱為高度平衡二元搜尋樹，任一節點對應的兩棵子樹的最大高度差為一，所以平常在新增和刪除節點的時候都需要對節點作旋轉，以保持樹的高度是否平衡。
上圖就是標準的AVL Tree，現在簡單示範如何旋轉節點達到平衡。

下圖明顯是高度(紅字)不平衡的二元搜尋樹。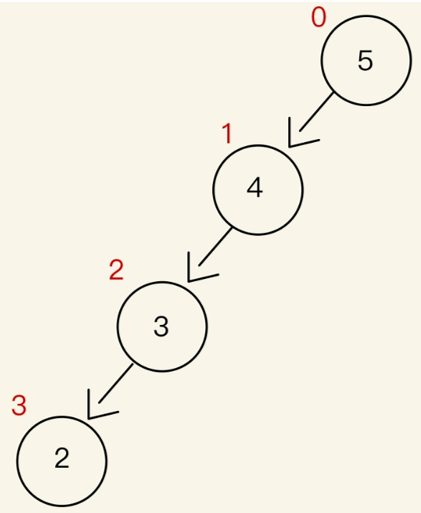

所以必須以3為中心點，順時針旋轉來達到樹的平衡。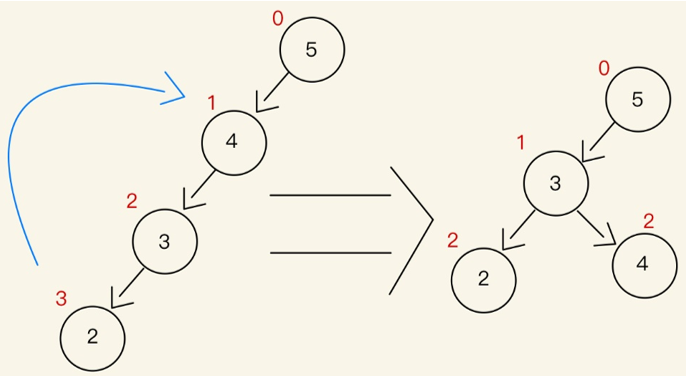

稍微介紹完就來實際建立一遍！
有很多程式與之前寫的Tree類似，可以從那邊複製過來。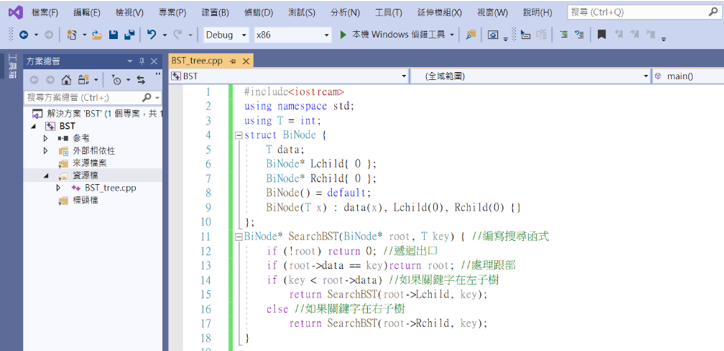

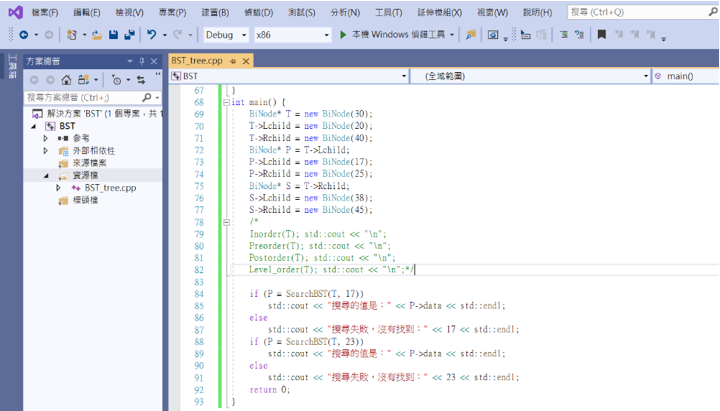
這樣就成功顯示出要搜尋的值和沒有搜尋到的值了。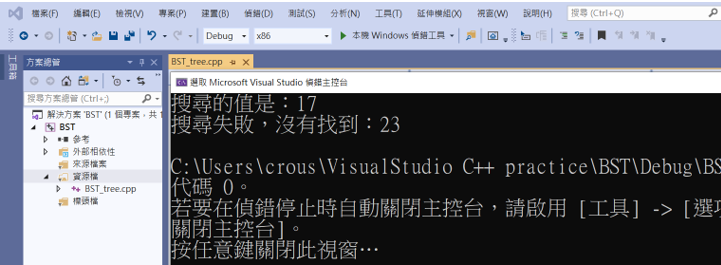

也可以利用疊代法找出想要的值。
疊代：重複回饋過程的活動，通常是為了接近並到達所需的目標或結果。每一次對過程的重複被稱為一次「疊代」，而每一次疊代得到的結果會被用來作為下一次疊代的初始值。

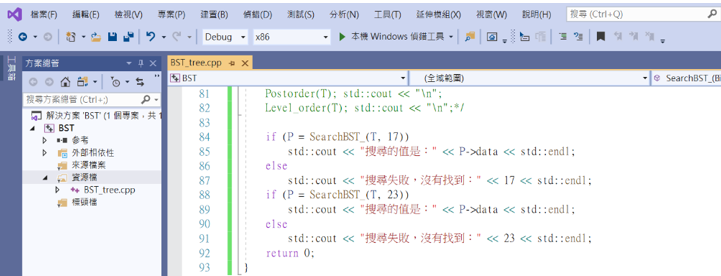
一樣可以得到相同的結果。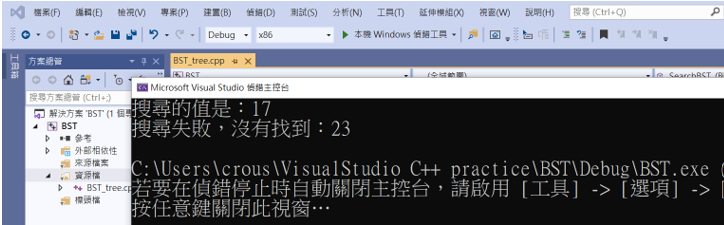

第一個方法是利用遞迴的方式一步步找到目標，而第二種方法是利用指針來找到想要的值。

接著來把二元搜尋樹寫得更完整！
先來實作插入節點。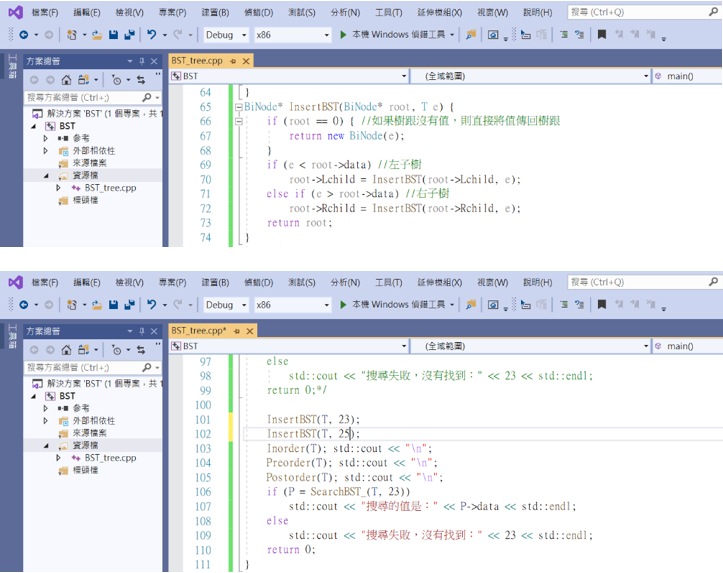

可以看到新增原本沒有的23，不僅排序沒有亂掉，而且有搜尋的到，還有新增原本就有的25也不會造成節點的值重複。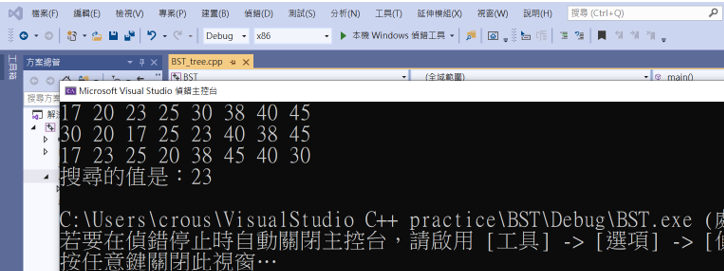

也同樣可以使用疊代法執行，因為結果都一樣，所以就不放上來了。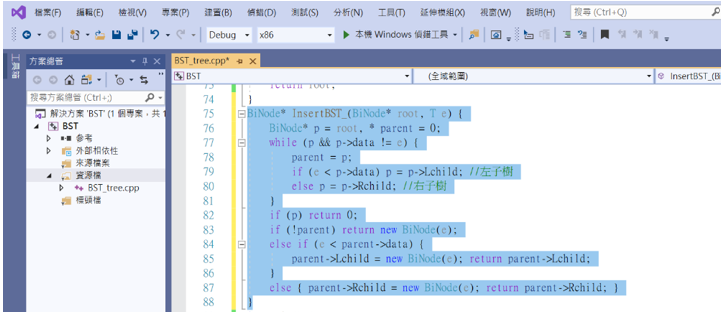

最後來做節點的刪除。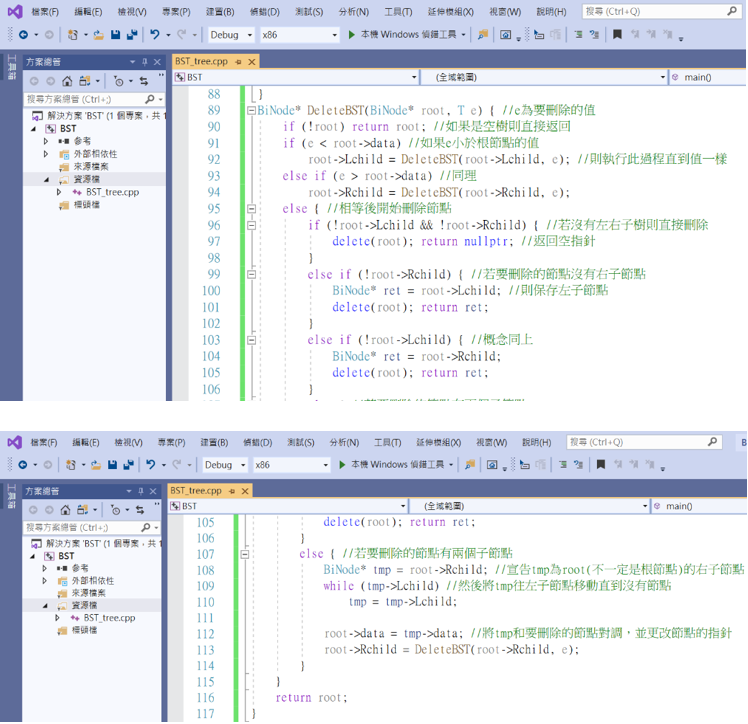

可以看到剛剛加入的23順利被刪除了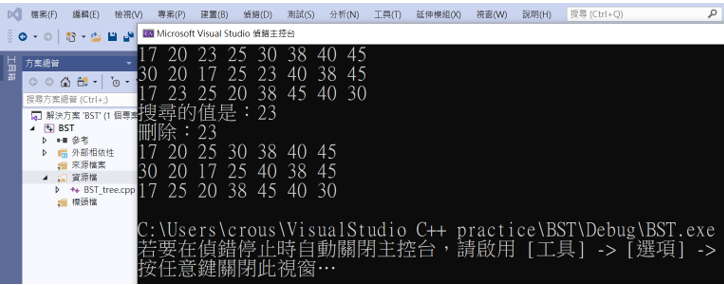

本日小結：呼~今天一口氣講完了二元搜尋樹，東西非常多要花幾天吸收也無訪，況且節點的刪除比較複雜，因為還得涉及刪除後子節點改指向誰，這部分一定要多加小心才不會出錯喔！明天會來介紹「雜湊」的搜尋法໒( ͡ᵔ▾ᵔ )७

參考連結：https://zh.wikipedia.org/zh-tw/%E8%BF%AD%E4%BB%A3#:~:text=%E7%96%8A%E4%BB%A3%E6%98%AF%E9%87%8D%E8%A4%87%E5%9B%9E%E9%A5%8B,%E7%96%8A%E4%BB%A3%E7%9A%84%E5%88%9D%E5%A7%8B%E5%80%BC%E3%80%82

#include<iostream>
using namespace std;
using T = int;
struct BiNode {
	T data;
	BiNode* Lchild{ 0 };
	BiNode* Rchild{ 0 };
	BiNode() = default;
	BiNode(T x) : data(x), Lchild(0), Rchild(0) {}
};
BiNode* SearchBST(BiNode* root, T key) { //編寫搜尋函式
	if (!root) return 0; //遞迴出口
	if (root->data == key)return root; //處理跟部
	if (key < root->data) //如果關鍵字在左子樹
		return SearchBST(root->Lchild, key);
	else //如果關鍵字在右子樹
		return SearchBST(root->Rchild, key);
}

BiNode* SearchBST_(BiNode*root,T key) { //利用疊代法找出想要的值
	BiNode* P = root;

	while (P && P->data != key)  //當P不是空的且P的值與關鍵字不同
		if (key < P->data) 
			P = P->Lchild; //將P改為P的左子節點
		else
			P = P->Rchild; //將P改為P的右子節點
		if (!P) return 0;
		return P;
	
}

void Inorder(BiNode* T) {
	if (!T)return;
	Inorder(T->Lchild);
	std::cout << T->data << " ";
	Inorder(T->Rchild);
}

void Preorder(BiNode* T) {
	if (!T) return;
	std::cout << T->data << " ";
	Preorder(T->Lchild);
	Preorder(T->Rchild);
}

void Postorder(BiNode* T) {
	if (!T)return;
	Postorder(T->Lchild);
	Postorder(T->Rchild);
	std::cout << T->data << " ";
}
#include<queue>
void Level_order(BiNode* T) {
	queue<BiNode*> Q;
	Q.push(T);
	while (!Q.empty()) {
		BiNode* p = Q.front();
		Q.pop();
		std::cout << p->data;
		if (p->Lchild) Q.push(p->Lchild);
		if (p->Rchild) Q.push(p->Rchild);
	}
}
BiNode* InsertBST(BiNode* root, T e) {
	if (root == 0) { //如果樹跟沒有值，則直接將值傳回樹跟
		return new BiNode(e);
	}
	if (e < root->data) //左子樹
		root->Lchild = InsertBST(root->Lchild, e);
	else if (e > root->data) //右子樹
		root->Rchild = InsertBST(root->Rchild, e);
	return root;
}
BiNode* InsertBST_(BiNode* root, T e) {
	BiNode* p = root, * parent = 0;
	while (p && p->data != e) {
		parent = p;
		if (e < p->data) p = p->Lchild; //左子樹
		else p = p->Rchild; //右子樹
	}
	if (p) return 0;
	if (!parent) return new BiNode(e);
	else if (e < parent->data) {
		parent->Lchild = new BiNode(e); return parent->Lchild;
	}
	else { parent->Rchild = new BiNode(e); return parent->Rchild; }
}
BiNode* DeleteBST(BiNode* root, T e) { //e為要刪除的值
	if (!root) return root; //如果是空樹則直接返回
	if (e < root->data) //如果e小於根節點的值
		root->Lchild = DeleteBST(root->Lchild, e); //則執行此過程直到值一樣
	else if (e > root->data) //同理
		root->Rchild = DeleteBST(root->Rchild, e);
	else { //相等後開始刪除節點
		if (!root->Lchild && !root->Rchild) { //若沒有左右子樹則直接刪除
			delete(root); return nullptr; //返回空指針
		}
		else if (!root->Rchild) { //若要刪除的節點沒有右子節點
			BiNode* ret = root->Lchild; //則保存左子節點
			delete(root); return ret;
		}
		else if (!root->Lchild) { //概念同上
			BiNode* ret = root->Rchild;
			delete(root); return ret;
		}
		else { //若要刪除的節點有兩個子節點
			BiNode* tmp = root->Rchild; //宣告tmp為root(不一定是根節點)的右子節點
			while (tmp->Lchild) //然後將tmp往左子節點移動直到沒有節點
				tmp = tmp->Lchild;

			root->data = tmp->data; //將tmp和要刪除的節點對調，並更改節點的指針
			root->Rchild = DeleteBST(root->Rchild, e);
		}
	}
	return root;
}
		
int main() {
	BiNode* T = new BiNode(30);
	T->Lchild = new BiNode(20);
	T->Rchild = new BiNode(40);
	BiNode* P = T->Lchild;
	P->Lchild = new BiNode(17); 
	P->Rchild = new BiNode(25);
	BiNode* S = T->Rchild;
	S->Lchild = new BiNode(38); 
	S->Rchild = new BiNode(45); 
	/*
	Inorder(T); std::cout << "\n";
	Preorder(T); std::cout << "\n";
	Postorder(T); std::cout << "\n";
	Level_order(T); std::cout << "\n";

	if (P = SearchBST_(T, 17))
		std::cout << "搜尋的值是：" << P->data << std::endl;
	else
		std::cout << "搜尋失敗，沒有找到：" << 17 << std::endl;
	if (P = SearchBST_(T, 23))
		std::cout << "搜尋的值是：" << P->data << std::endl;
	else
		std::cout << "搜尋失敗，沒有找到：" << 23 << std::endl;
	return 0;*/

	InsertBST(T, 23);
	InsertBST(T, 25);
	Inorder(T); std::cout << "\n";
	Preorder(T); std::cout << "\n";
	Postorder(T); std::cout << "\n";
	if (P = SearchBST_(T, 23))
		std::cout << "搜尋的值是：" << P->data << std::endl;
	else
		std::cout << "搜尋失敗，沒有找到：" << 23 << std::endl;

	std::cout << "刪除：" << 23 << endl;
	T = DeleteBST(T, 23);
	Inorder(T); std::cout << "\n";
	Preorder(T); std::cout << "\n";
	Postorder(T); std::cout << "\n";
	return 0;
}