前言：昨天講解完了堆積的概念，今天要來實際操作一遍，在查找資料之餘，有發現一個有趣的ACM程式競賽題，實作完堆積後會順便介紹給各位看看。

堆疊的向下調整：

昨天有提到堆積調整的概念及方法，現在就是要來實踐的時候！

向下調整通常在一開始建立堆積的時候或刪除元素的時候會執行。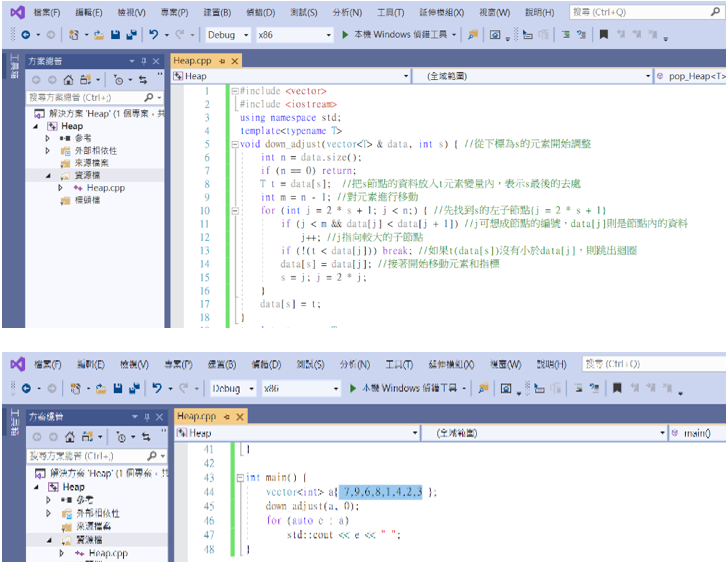

可以看到堆積內的元素已經調整完成，詳細圖形如下。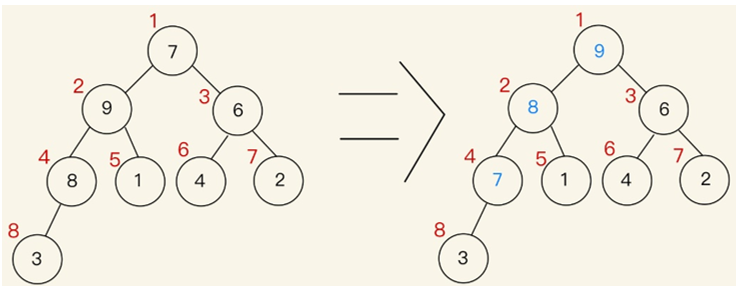

撰寫好向下調整的方法後，還可以再寫一個把雜亂無章的數組調整成堆積的方法。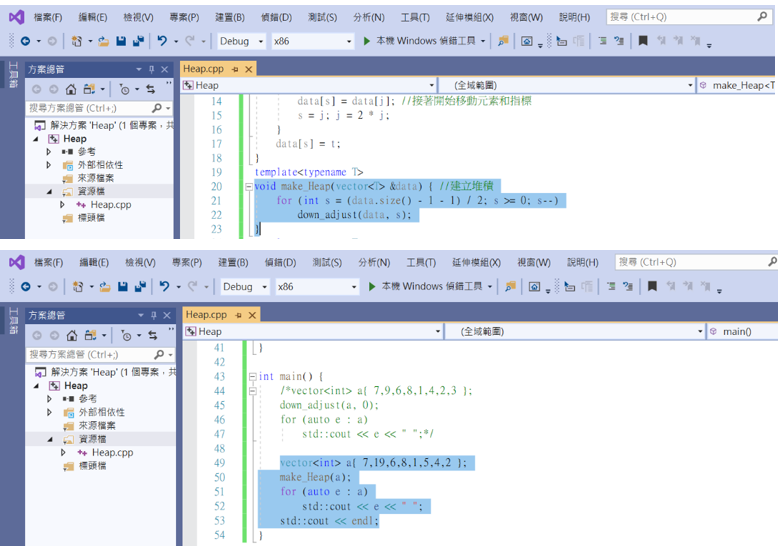

接著來寫刪除元素的方式，並直接調整維持堆疊的規則。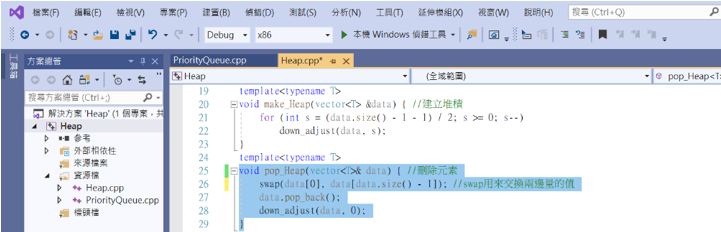

再來撰寫新增元素的方法，且直接向上調整成堆疊。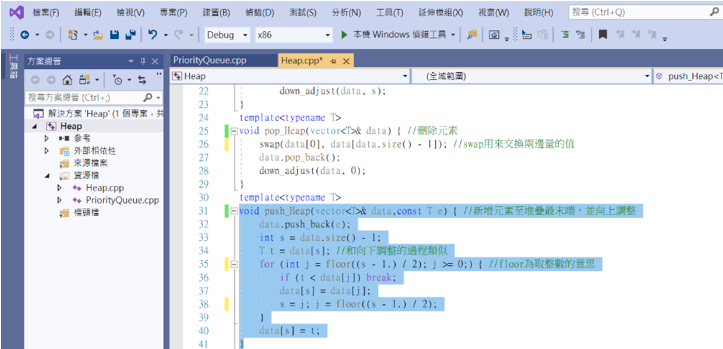

輸出結果，第一行為原本的堆疊，第二行為新增11，第三行則刪除堆疊頂端。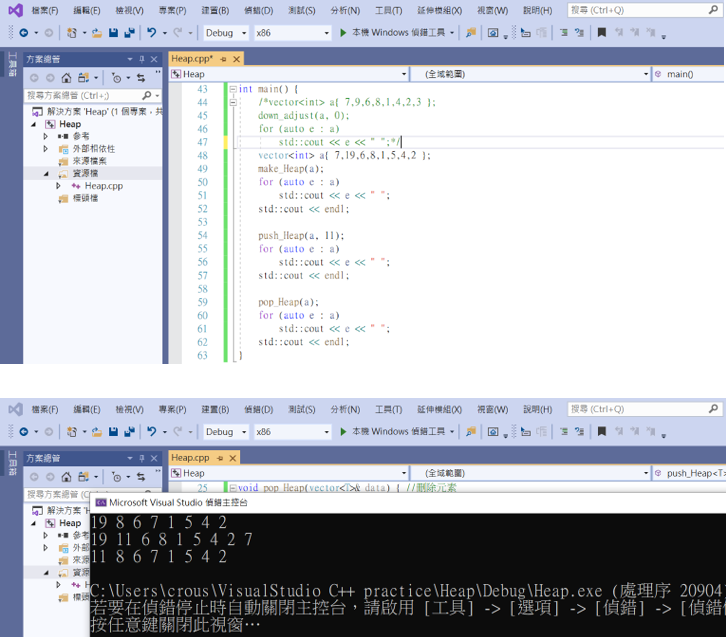

利用堆疊實作優先佇列：

掌握了堆疊，接著可以練習看看優先佇列的建立。
提示：把堆疊想像成優先佇列，新增就是push，刪除就是pop，堆疊頂端就是最優先元素。直接往下繼續寫就好oUo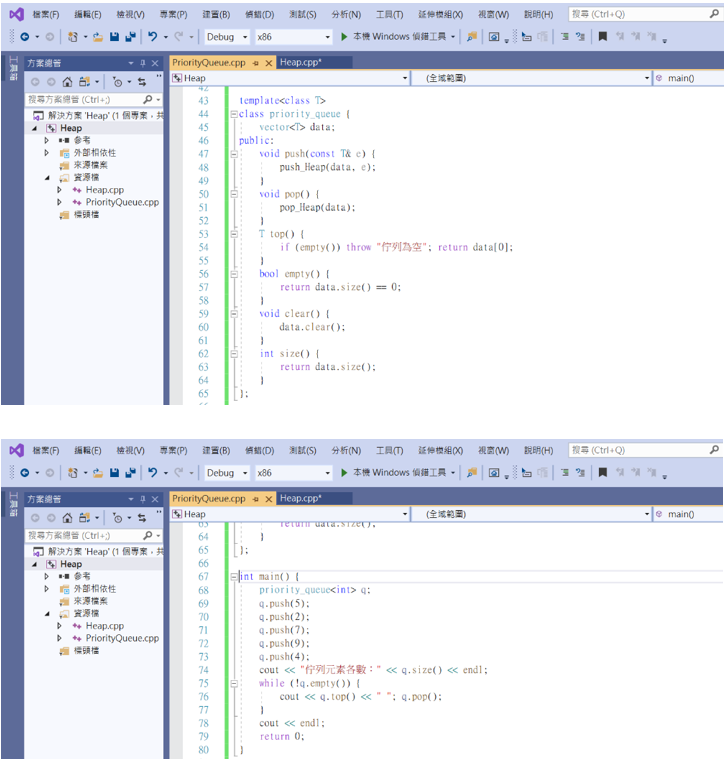

這樣就不需依靠C++內部的程式完成優先佇列。

ACM競賽題 – 聰明的木匠：在查找資料過程中，意外找到了著個題目，就順便分享一下
題目內容：一位木匠需要將一根長的木棒切成N段。每段的長度分別為L1,L2,......,LN（1 <= L1,L2,…,LN <= 1000，且均為整數）個長度單位，且切割時僅在整數點處切且沒有木材損失。
木匠發現，每一次切割花費的體力與該木棒的長度成正比，設切割長度為1的木棒花費1單位體力。例如：若N=3，L1 = 3,L2 = 4,L3 = 5，則木棒原長為12，木匠可以有多種切法，如：先將12切成3+9.，花費12體力，再將9切成4+5，花費9體力，一共花費21體力；還可以先將12切成4+8，花費12體力，再將8切成3+5，花費8體力，一共花費20體力。顯然，後者比前者更省體力。那麼，木匠至少要花費多少體力才能完成切割任務呢？

執行結果如下，第一行為n的值，第二行為每此切割次數的長度，接著就是計算結果。

本日小結：今天也是非常充實的一天，終於結束了堆疊的部分，下一次提到大概就是演算法的時候了，木匠的程式碼雖然不長，但是要理解題目的內容就要花點時間了，如果還是不懂也沒關係，先把基礎的弄明白就好了⋋╏ ❛ ◡ ❛ ╏⋌

堆積

#include <vector>
#include <iostream>
using namespace std;
template<typename T>
void down_adjust(vector<T> & data, int s) { //從下標為s的元素開始調整
	int n = data.size();
	if (n == 0) return;
	T t = data[s];  //把s節點的資料放入t元素變量內，表示s最後的去處
	int m = n - 1; //對元素進行移動
	for (int j = 2 * s + 1; j < n;) { //先找到s的左子節點{j = 2 * s + 1}
		if (j < m && data[j] < data[j + 1]) //j可想成節點的編號，data[j]則是節點內的資料
			j++; //j指向較大的子節點
		if (!(t < data[j])) break; //如果t(data[s])沒有小於data[j]，則跳出迴圈
		data[s] = data[j]; //接著開始移動元素和指標
		s = j; j = 2 * j;
	}
	data[s] = t;
}
template<typename T>
void make_Heap(vector<T> &data) { //建立堆積
	for (int s = (data.size() - 1 - 1) / 2; s >= 0; s--)
		down_adjust(data, s);
}
template<typename T>
void pop_Heap(vector<T>& data) { //刪除元素
	swap(data[0], data[data.size() - 1]); //swap用來交換兩邊量的值
	data.pop_back();
	down_adjust(data, 0);
}
template<typename T>
void push_Heap(vector<T>& data,const T e) { //新增元素至堆疊最末端，並向上調整
	data.push_back(e);
	int s = data.size() - 1;
	T t = data[s]; //和向下調整的過程類似
	for (int j = floor((s - 1.) / 2); j >= 0;) { //floor為取整數的意思
		if (t < data[j]) break;
		data[s] = data[j];
		s = j; j = floor((s - 1.) / 2);
	}
	data[s] = t;
}

int main() {
	/*vector<int> a{ 7,9,6,8,1,4,2,3 };
	down_adjust(a, 0);
	for (auto e : a)
		std::cout << e << " ";*/
	vector<int> a{ 7,19,6,8,1,5,4,2 };
	make_Heap(a);
	for (auto e : a)
		std::cout << e << " ";
	std::cout << endl;

	push_Heap(a, 11);
	for (auto e : a)
		std::cout << e << " ";
	std::cout << endl;

	pop_Heap(a);
	for (auto e : a)
		std::cout << e << " ";
	std::cout << endl;
}

優先佇列

#include <vector>
#include <iostream>
using namespace std;
template<typename T>
void down_adjust(vector<T>& data, int s) { //從下標為s的元素開始調整
	int n = data.size();
	if (n == 0) return;
	T t = data[s];  //把s節點的資料放入t元素變量內，表示s最後的去處
	int m = n - 1; //對元素進行移動
	for (int j = 2 * s + 1; j < n;) { //先找到s的左子節點{j = 2 * s + 1}
		if (j < m && data[j] < data[j + 1]) //j可想成節點的編號，data[j]則是節點內的資料
			j++; //j指向較大的子節點
		if (!(t < data[j])) break; //如果t(data[s])沒有小於data[j]，則跳出迴圈
		data[s] = data[j]; //接著開始移動元素和指標
		s = j; j = 2 * j;
	}
	data[s] = t;
}
template<typename T>
void make_Heap(vector<T>& data) { //建立堆積
	for (int s = (data.size() - 1 - 1) / 2; s >= 0; s--)
		down_adjust(data, s);
}
template<typename T>
void pop_Heap(vector<T>& data) { //刪除元素
	swap(data[0], data[data.size() - 1]);
	data.pop_back();
	down_adjust(data, 0);
}
template<typename T>
void push_Heap(vector<T>& data, const T e) { //新增元素至堆疊最末端，並向上調整
	data.push_back(e);
	int s = data.size() - 1;
	T t = data[s]; //和向下調整的過程類似
	for (int j = floor((s - 1.) / 2); j >= 0;) { //floor為取整數的意思
		if (t < data[j]) break;
		data[s] = data[j];
		s = j; j = floor((s - 1.) / 2);
	}
	data[s] = t;
}

template<class T>
class priority_queue {
	vector<T> data;
public:
	void push(const T& e) {
		push_Heap(data, e);
	}
	void pop() {
		pop_Heap(data);
	}
	T top() {
		if (empty()) throw "佇列為空"; return data[0];
	}
	bool empty() {
		return data.size() == 0;
	}
	void clear() {
		data.clear();
	}
	int size() {
		return data.size();
	}
};
template<typename T>
void heapsort_down_adjust(vector<T>& data, int s,int m) { //從下標為s的元素開始調整
	T t = data[s];  //把s節點的資料放入t元素變量內，表示s最後的去處
	for (int j = 2 * s + 1; j <= m;) { //先找到s的左子節點{j = 2 * s + 1}
		if (j < m && data[j] < data[j + 1]) //j可想成節點的編號，data[j]則是節點內的資料
			j++; //j指向較大的子節點
		if (!(t < data[j])) break; //如果t(data[s])沒有小於data[j]，則跳出迴圈
		data[s] = data[j]; //接著開始移動元素和指標
		s = j; j = 2 * j;
	}
	data[s] = t;
}
template<typename T>
void heap_sort(vector<T>& data){
	int n = data.size();
	for (int s = floor((data.size() - 1 - 1) / 2); s >= 0; s--) //建立堆疊
		heapsort_down_adjust(data, s, n - 1); //s~n-1之間
	for (int i = n - 1; i > 0; i--) {
		swap(data[0], data[i]); //交換兩元素
		heapsort_down_adjust(data, 0, i - 1); //0~i-1之間
	}
}
int main() {
	/*priority_queue<int> q;
	q.push(5);
	q.push(2);
	q.push(7);
	q.push(9);
	q.push(4);
	cout << "佇列元素各數：" << q.size() << endl;
	while (!q.empty()) {
		cout << q.top() << " "; q.pop();
	}
	cout << endl;
	return 0;*/

	vector<int> a{ 7,9,2,8,1,4,6,3 };
	heap_sort(a);
	for (auto e : a)
		std::cout << e << " ";
	std::cout << endl;
}

聰明的木匠

#include<iostream>
#include<queue>
#include<vector>
using namespace std;

int main() {
	std::priority_queue<int, std::vector<int>, std::greater<int> >q;
	//因為每此都要先取小的，所以使用優先佇列
	int n;
	while (cin >> n) { //輸入n，為要切幾此
		for (int i = 0; i < n; i++) {
			int key; //key為每次切割的長度
			std::cin >> key;
			q.push(key); //放入佇列
		}
		int sum = 0;
		while (n >= 2) {
			int a, b;
			a = q.top(); //先從佇列取一個最小的
			q.pop();
			b = q.top(); //在取第二小的
			q.pop();
			q.push(a + b); //把相加的結果在放入佇列中
			sum += a + b; //因為相加的結果必須要參加下一階段
			cout << a << " " << b << " " << sum << std::endl;
			n--; //每執行完一次循環就將n-1
		}
		cout << sum << endl;
	}
	return 0;
}