前言：之前談到的方法都需要透過「關鍵字」的比較來找出想要的值，但是雜湊法與之前的搜尋法有些差異，究竟是甚麼原因讓雜湊法如此特別，想知道原因就繼續看下去吧！

甚麼是雜湊法？
基本上雜湊法就是將原本的資料經過一個特殊的公式所產生的產物，以便後續的利用，而這個特殊的公式稱為雜湊函式，產物則稱為雜湊值。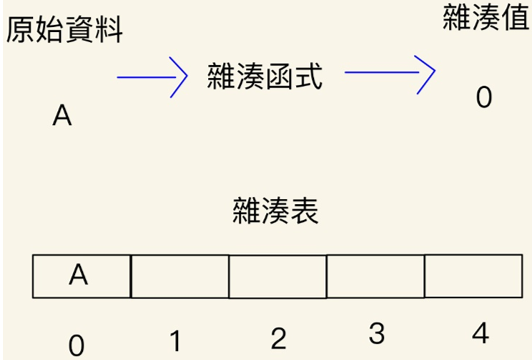

雜湊值最常用來當作儲存原始資料的地址於雜湊表中，且雜湊值是不可逆的，無法將雜奏值推算回原始資料，也就是說如果沒有雜湊表只有雜湊值是沒有任何意義的。

雜湊的應用：第一個就是今天的重點雜湊表，再來因為雜湊值不可逆的關係起到保護資料的效果，其他也有語音辨識、錯誤校正等多種應用方式。

雜湊法名詞整理：

介紹完了定義和應用，再把容易混淆的名詞釐清吧！

雜湊函數 (Hashing Function)
可將資料轉換成資料儲存位址的公式。

雜湊值 (Hash Code)
原始資料經過雜湊函數所計算的結果，計算出來的結果無法回推原始資料。

雜湊表 (Hash Table)
為連續的記憶體，用來儲存原始資料，類似一種索引表格，可根據雜湊值直接查詢儲存資料的位址。(可分為多個桶)

桶 (Bucket)
雜湊表中儲存資料的地方，每一筆資料都對應到唯一的一個位址 (Bucket Address)。(可分為多個槽)

槽 (Slot)
每一筆資料種可會有好幾個欄位，而「槽」就是指「桶」中的欄位。

碰撞 (Collision)
若多筆不同的資料，經過雜湊函數運算後得到相同的位址(雜湊值一樣)，則會使用到同一個Bucket。

溢位 (Overflow)
資料經過雜湊函數的計算後，如果桶已經被其它資料存滿，則此筆資料無法儲存在該位址，會使Bucket發生溢位。

同義字 (Synonym)
當兩個識別字經雜湊函式計算後得到相同的數值時，則稱這兩個識別字與此湊函式是同義字。

載入密度 (Loading Factor)
指識別字的使用數目除以雜湊表內槽的總數。
公式：α(載入密度)=s(每一個桶內的槽數)b(桶的數目)

完美雜湊 (Perfect Hashing)
指沒有碰撞和溢位的雜湊函式。

設計雜湊函式須注意的事：

1. 降低碰撞和溢位的發生。
2. 不要太過複雜，越容易計算越好。
3. 儘量把文字的鍵值轉成數字的鍵值，以方便計算。
4. 得到的雜湊值盡量均勻的分佈在各個桶內，不要太過於集中。

雜湊函式的常見類型：

沒有特別規定必須要用哪種方法，只要多加注意溢位和碰撞的問題即可。

除法 (Mod /Division)
最簡單的雜湊函式，將資料除以一個常數後，取於數來當雜湊值索引。

中間平方法 (Middle Sequare)
和除法類似，先講資料乘上自己，在取中間的某段數字當作雜湊值索引。

折疊法 (Folding Addition)
將資料轉換成一串數字後，在將這串數字分成多個部分，最後再相加起來。
可分為兩種移動折疊法 (Shift Folding)和邊界折疊法 (Boundary Folding)。

數位分析法 (Digits Analysis)
適用於資料都會更改的數字型靜態表，在決定雜湊函式時會先檢查資料的相對位置和分布情形，將重複性高的部分刪除。

碰撞問題及溢為處理：

線性探測法 (Linear Probing)
當發生碰撞時，若該雜湊值已有資料，則以線性的方式往後尋找空的儲存位置，一找到就將資料放入。這種方法通常把雜湊視為環狀結構，一旦後面的位置被填滿而前面還有位置時，可以將資料往前放。

平方探測法 (Quadratic Probing)
若發生溢位，可以代入公式 ，H(x)代表雜湊值，b為資料可儲存在桶中的數量，i=1,2,3,4….持續增加，若i代入1還是有溢位，則將i代入2，以此類推。

再雜湊法 (Rehashing)
當使用第一種雜湊函式發生一位時，則準備第二種雜奏函式，若還是有溢位則再使用第三個，直到沒有溢位為止。

連結串列 (Chaining)
將雜湊表的所有空間(桶)都建立成串列，如果發生溢位，則把一開始的串列當成列首，多出來的資料接在後方即可。

一樣沒有特定的方法處理溢位，如果雜湊函式和溢位處理的種類有那裡不懂的可以查查看網路上的範例，會比較好理解。

本日小結：今天的資訊量已經很多了，在繼續講下去恐怕效果會不好，明天再來實作雜湊的內容，因為之前有學過鏈結串列，所以會用串列法來實作，忘記的人可以回去看看！