在昨天的文章中，我們介紹 Netflix 在測試新功能「顯示Top 10 的節目排名」頁面時，使用 A/B testing。在搜集完資料後，資料科學家要如何判斷新功能是否有成功提升用戶參與度呢？

答案的選項只有兩個：是或否。

根據數據，資料科學家會判斷出一個結果。然而，世界上沒有任何一個方法可以完全消除不確定性和犯錯的可能性。

可能犯的兩種錯誤

• False positive（Type I error）：當資料顯示兩者有差異，但事實上沒有。
  e.g., 當實驗結果顯示 Top 10 會讓用戶參與度提升，但事實上沒有。
• False negative（Type II error）：當資料顯示兩者沒有差異，但事實上有。
  e.g., 當實驗結果顯示 Top 10 不會讓用戶參與度提升，但事實上有提升。

我們不可能同時消除兩種錯誤，因為兩者會互相 trade-off。
不過，認識這兩種錯誤的形成原因是很重要的，可以讓我們更了解實驗的結果。

今天，我們來聊聊這兩種錯誤吧！

（以下會介紹基本的統計觀念，會盡量以淺顯易懂的例子說明，如果有任何不懂之處也歡迎發問。）

Type I error: False Positive (α)

在設計 A/B testing 時，通常會以設定 false positive 為起點。

習慣上，false positive rate 會被設定為 0.05，意即在實際上 A 組和 B 組無差異的情況下，會有 5% 的情況我們會錯誤地認為 A 和 B 是有差異的。而在統計上，稱這種情況為 5% 的顯著水準（siginificance level）。

以本次實驗為例，犯下 Type I error 的狀況是：新增 Top 10 排名實際上不會提升用戶參與度，但是我們錯誤地認為能夠提升參與度。

p-value

Type I error 和 p-value 的關係很緊密，p-value 是看到和 A/B testing 結果一樣極端的機率值（the probability of seeing an outcome at least as extreme as our A/B test result）。

這句話實在太複雜，我們用一個直覺一點的例子來思考。

假設一個箱子中有許多黑球和白球，在兩邊數量相同的情況下，抽出黑球的機率是 50%。而假設黑球數量較較多的話，抽出黑球的機率應該會大於 50%。
這個推論非常直觀，也跟 Netflix 研究用戶行為有非常大的關聯，有些用戶行為是二元問題，例如是否點擊按鈕、是否繼續訂閱。

接下來，我們執行一個實驗，反覆在箱子中抽一百次球，取後放回，看總共抽到黑球幾次。即使黑球和白球的數量相同，也可能不會剛好是黑白球各五十次。究竟要抽到多少次黑球，才能視為黑白球的數量不同呢？六十次？還是七十次？

這個其實就是在做 A/B testing 時，我們想要問的問題，究竟要抽到黑白球的次數差異多少，兩球才能夠視為數量不同呢？

Null Hypothesis

在回答上面問題之前，我們先想像一個比較簡單的版本。

首先，我們假設黑白球的數量相同，意即抽到黑球的機率為 50%。這個假設在統計上被稱為「虛無假設（null hypothesis）」。

再來，我們擴大實驗規模，將這一個抽球實驗重複一千次（i.e., 每次實驗都會在箱子抽一百次球，取後放回，再紀錄本次抽到黑球的數量），可以繪製出如下的圖形：

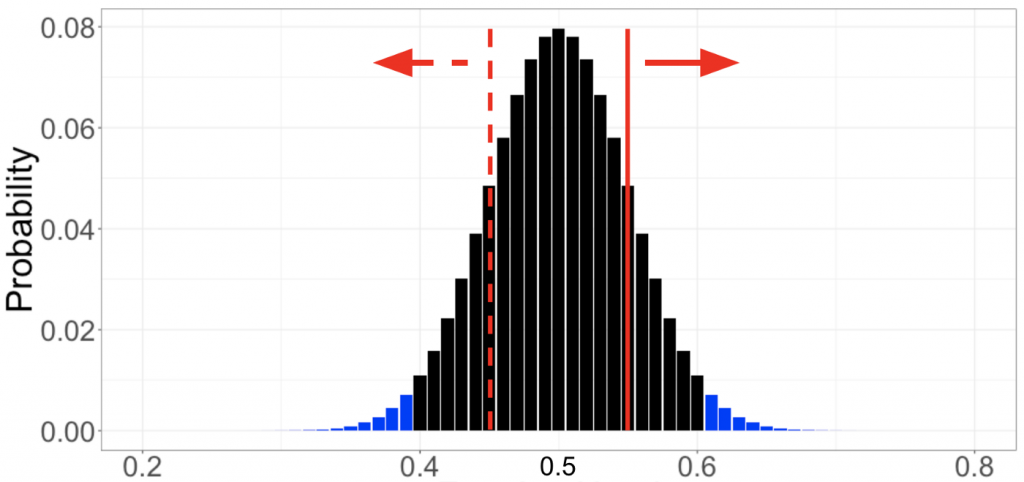
這個分布被稱為 null distribution。
橫軸表示每次實驗抽到的黑球比例，縱軸則是在一千次中，這個比例佔了多少。舉例而言，抽到 50 顆黑球的次數有 80 次，因此在橫軸為 0.5 (= 50/100) 的那條 bar 之高度為 0.08 (= 80/1000)。

最後，我們再執行一次抽球實驗，此次實驗中有 55 次抽到黑球。

為了確定黑白球數量是否一致，回想上述 p-value 的定義「和 A/B testing 結果一樣極端的機率值（the probability of seeing an outcome at least as extreme as our A/B test result）」。

白話一點的翻譯就是：我們要將比抽樣結果更不可能發生事件之所有機率加總。

在這次實驗中我們沒有假設黑白球哪一種可能比較多，因此直接將大於 0.55（假設黑球數量較多） 和小於 0.45（假設白球數量較多）所有 bar 的高度加總，此數值即為 p-value。

好，喘口氣，我們算出 p-value 了，但是這跟 0.05 的 false positive rate 有什麼關係呢？

在統計上，若 p-value 小於 0.05，則可以「拒絕虛無假設」。以本次實驗來說，p-value 為 0.32，沒有小於 0.05，因此我們不能說箱子中黑白球的數量是不同的。

以更淺白的方式來說，p-value 是在 null distribution 看到這筆在真實世界看到的資料之機率，假設 p 為 0.01，代表在 null distribution 看到這個機率很小，所以可以推翻虛無假設。

因為在 null distribution 發生的機率太小了，但我們在現實中觀察到了，所以代表虛無假設是錯的。

回到 A/B testing 中，會有兩種結論：

1. 操弄的變項是有用的。
   e.g., 黑白球的數量不同、放置 Top 10 排名有助於提高用戶參與度。
2. 沒有足夠的證據支持此操弄變項有用。
   e.g., 沒有足夠證據證明黑白球的數量相等、沒有足夠證據支持放置 Top 10 排名有助於提高用戶參與度。

值得注意的是，第二種結論中，用詞是「沒有足夠證據」，而非「沒有用」。
因為這個理論沒有辦法支持我們論述什麼變因沒有用，我們只能說**「沒有蒐集到足夠的證據」證明黑白球的數量不同**。但是，不代表我們可以推論黑白球的數量是相同的，也許在搜集更多證據，意即抽更多次球後，我們能夠拒絕虛無假設也說不定。

由於怕大家難以消化，false negative 的部分留待明天介紹。
今天的內容較長，統計觀念對於初次接觸的人也較複雜。如果太難理解的話可以多看幾次、好好思考消化，有問題也歡迎發問。

我們明天見！

謝謝讀到最後的你，如果喜歡這系列，別忘了按下喜歡和訂閱，才不會錯過最新更新。
也歡迎到我的 medium 逛逛！

Reference:

• Interpreting A/B test results: false positives and statistical significance: https://netflixtechblog.com/interpreting-a-b-test-results-false-positives-and-statistical-significance-c1522d0db27a
• Interpreting A/B test results: false negatives and power: https://netflixtechblog.com/interpreting-a-b-test-results-false-negatives-and-power-6943995cf3a8