在昨天的文章中，我們執行了一個抽球的想像實驗，讓我們來回憶一下

在不知道箱子中黑白球數量的情況下，藉由抽球實驗想要確定兩球之數量：

(1) 虛無假設（null hypothesis）：假設箱子中黑白球的數量相同。
(2) 設定 false positive rate (α) 為 0.05。
(2) 反覆在箱子中抽一百次球，取後放回，看總共抽到黑球幾次。
(3) 擴大實驗規模，將這一個抽球實驗重複一千次（i.e., 每次實驗都會在箱子抽一百次球，取後放回，再紀錄本次抽到黑球的數量），可以繪製出如下被稱為 null distribution 的分佈：

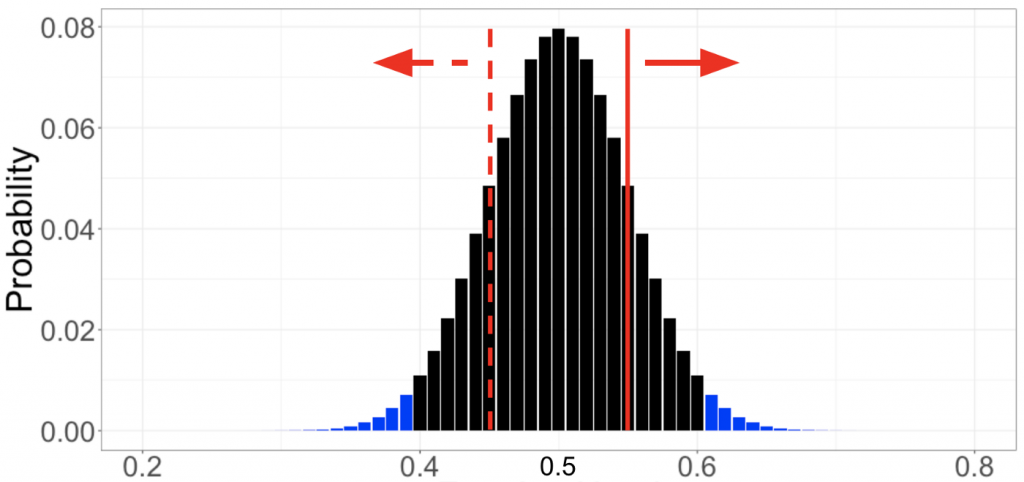
(4) 最後，我們再執行一次抽球實驗，此次實驗中有 55 次抽到黑球。
(5) 將大於 0.55（假設黑球數量較多） 和小於 0.45（假設白球數量較多）所有 bar 的高度加總，得到 p-value 為 0.32。
(6) 由於 p-value (0.32) > α (0.05)，因此無法拒絕虛無假設，黑白球的數量是相等的。

如果以 Netflix 的 A/B testing 為例，結論會是新舊頁面對用戶參與度沒有影響。

再介紹兩個名詞：rejection region 和 confidence level。

1. Rejection region：可以拒絕虛無假設，也就是可以說黑白球數量不同之處。其位置座落於圖中的藍色區域，以 siginificance level 設定為 0.05 為例，左右半邊之藍色區域的 bar 高度加總各為 0.025
2. Confidence level：無法拒絕虛無假設之處，在上圖中兩條紅色線之間。

好，以上是 false positive 的介紹。
再來回顧一下可能犯下的兩種錯誤類型：

• False positive（Type I error）：當資料顯示兩者有差異，但事實上沒有。
  e.g., 當實驗結果顯示 Top 10 會讓用戶參與度提升，但事實上沒有。
• False negative（Type II error）：當資料顯示兩者沒有差異，但事實上有。
  e.g., 當實驗結果顯示 Top 10 不會讓用戶參與度提升，但事實上有提升。

Type II error: False Negative

至於 false negative 則是在 A 組和 B 組有差異的情況下，資料卻顯示他們沒有差異。

False negative rate = 1 - power

Power

在思考 power 是什麼之前，我們先回到箱子抽球的例子。

這次假設黑白球的數量不同（假設黑球的數量佔 64%，意即被抽到的機率為 64%），跟前次實驗一樣，我們不會預期執行一個抽一百次球的實驗時，一定會抽到 64 次黑球。按照上次的實驗步驟，將一個實驗執行一千次，可以繪製如下圖所示的圖：

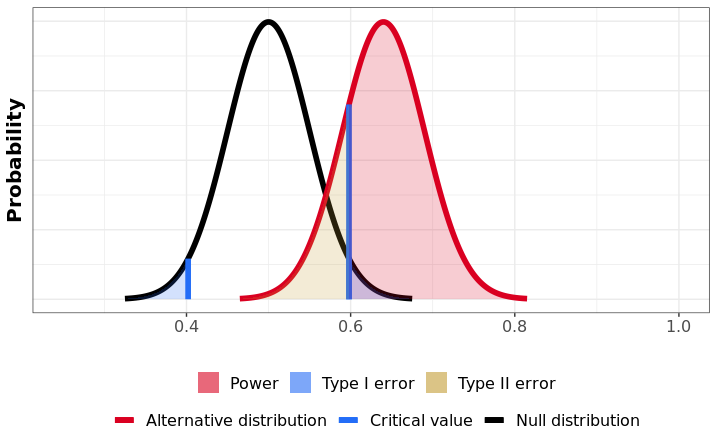
視覺上來說，power 就是 critical value（0.05 的顯著水準）的右邊、在紅線底下佔的面積。

也就是說，在事實上有 64% 的黑球在箱子的前提下，重複執行抽一百次球的實驗。
若顯著水準設為 0.05，有 80% 的機會能夠成功拒絕虛無假設（拒絕黑白球的數量相同的假設），而另外 20% 會犯下 false negative 的錯誤。

兩個可能會影響 type 2 error 的事情：

• the effect size：真實母體參數值和在虛無假設中假設的數值，差異越大，越容易發現。
• 樣本大小（the sample size）：當樣本數 n 變大，會讓抽樣分佈變窄，進而讓 null hypothesis 和抽樣分佈（sampling distribution）的重疊變小。
  樣本數變大，更容易發現差異。在實際應用上，若增加每組的樣本，就需要減少實驗組的數量，也是一種 trade-off。

以上，兩種錯誤有關的統計觀念討論完畢，這些統計判斷對於資料科學是很重要的事，才能夠有足夠的能力解讀實驗數據哦。
大家明天見！

謝謝讀到最後的你，如果喜歡這系列，別忘了按下喜歡和訂閱，才不會錯過最新更新。
也歡迎到我的 medium 逛逛！

Reference:

• Interpreting A/B test results: false negatives and power: https://netflixtechblog.com/interpreting-a-b-test-results-false-negatives-and-power-6943995cf3a8