根據過去的資料來預測決策的樹狀圖,因為決策過程被視覺化,常被用來解釋決策的原因。
比如說租屋公司想要靠過去的資料預測怎樣的公寓條件比較容易租給年輕人。
部分資料:
| 公寓樓層 | 房間大小(坪數) | 幫收垃圾服務 | 租或不租 |
|---|---|---|---|
| 5 | 15 | 有 | 不租 |
| 5 | 12 | 沒有 | 不租 |
| 3 | 10 | 有 | 租 |
| 1 | 8 | 沒有 | 不租 |
程式依照給的資料畫出的決策樹。
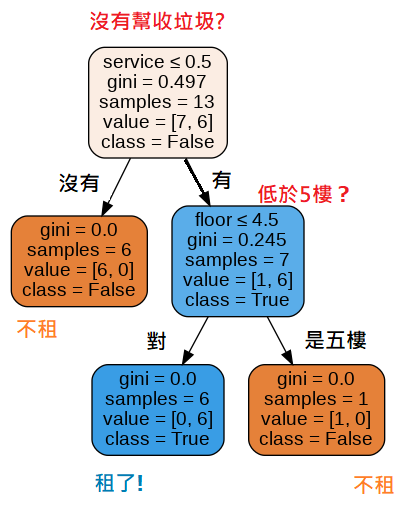
可以看到沒有幫收垃圾服務就不租,有幫收垃圾,但在5樓要爬樓梯就不租,得出有幫收垃圾服務且低於5樓比較容易出租的結論。
不過當資料越多,決策樹做越多層,會有過度擬合的狀況發生,這邊用圖示來示範比較好理解。
決策樹限制深度為2層時分類結果長這樣,看起來雖然有一點分類錯誤,但整體的分類看起來是合理的。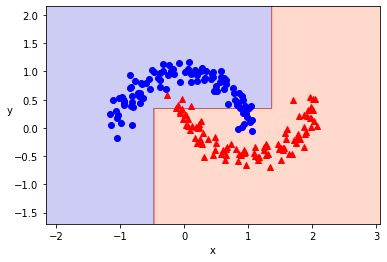
但是做到6層的話,如同下面的圖,變成硬要把已知的分類都分清楚,反而導致對未知資料的分類準確度下降。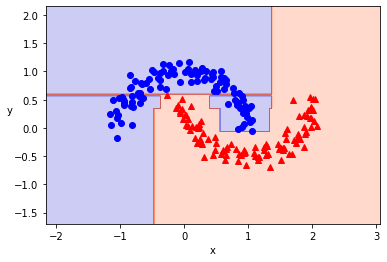
單個決策樹的預測率通常只有60%~80%的準確率,被稱為弱學習器。所以不常使用單個決策樹,而是採用集成學習,使用複數個弱學習器組合成一個準確率較高的強學習器來預測。
使用複數模型來學習的方式。通常會比使用單個模型的預測效果要好
下面的隨機森林和梯度提升都是集成學習的一種。
由很多決策樹隨機組成的森林。
隨機森林的步驟如下:
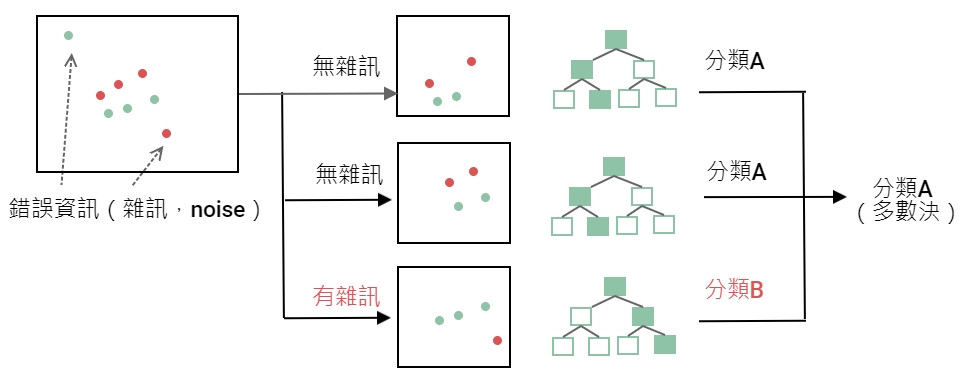
之所以只取一部份資料是因為可以隨機避開錯誤的資訊。讓整體的分類更精確,比較難發生過度擬合的問題。而隨機森林屬於集成學習的袋裝法。
只取一部份資料讓複數模型做學習。而取出來的樣本會放回去讓其他模型可以重複使用叫做自助法(Bootstrapping)。所以袋裝法又被稱為自助聚合法(Bootstrap Aggregation)。
屬於集成學習的提升法。最佳化則是使用梯度下降法所以叫梯度提升。模型通常也是使用決策樹。
梯度提升的步驟如下:
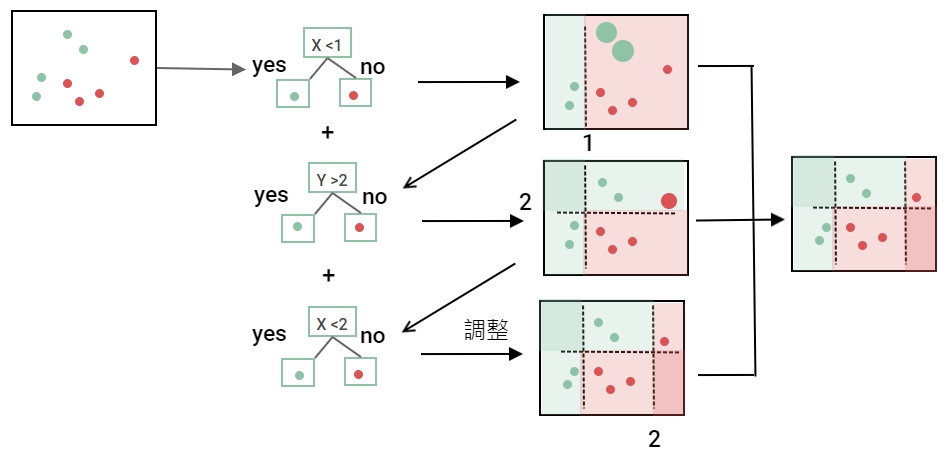
提升法和袋裝法很像,都是使用多個模型然後只使用一部份的資料做學習。差別在於提升法的模型有先後順序,一個計算完換下一個,而袋裝法的模型可以同時並行做計算。所以袋裝法速度較快,提升法速度較慢。但相對地提升法有持續做修正預測比較精準。
梯度下降是一個對機器學習和深度學習都非常重要的演算法,主要是用來做最佳化,也就是最小化損失(Loss),達到讓誤差最小。
前面有說到線性回歸做最佳化是使用最小平方法,但是大多數的時候不是像線性回歸這麼簡單靠公式就能找到最小誤差。所以這時候就會使用梯度下降來找出最佳解。為了簡單解說我們先假設只有一個參數 w 來求最小損失,我們怎麼知道找出讓 Loss 最小的 w?以下面的圖而言就是求斜率。
你可以想像成登山者去山谷下的營地(Loss=0)。可以透過山坡的斜率知道朝哪個方向是下山的路。
| 斜率>0:往負的方向走 | 斜率<0:往正的方向走 |
|---|---|
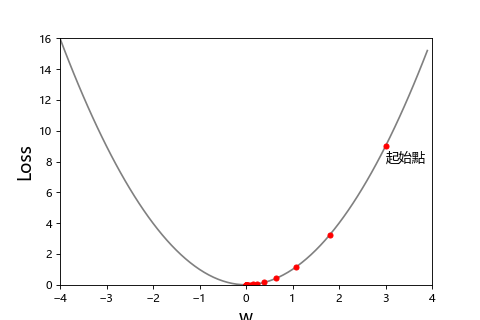 |
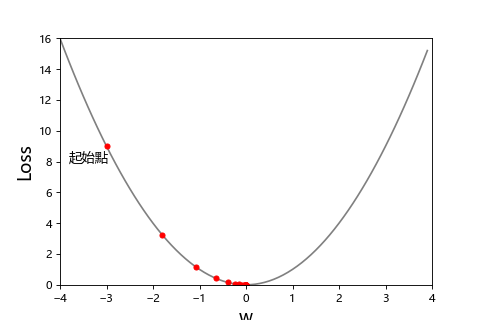 |
求一個參數的最小化損失是使用2維平面求斜率,那多個參數呢,就是多維空間求梯度,梯度一樣是斜率,只是下山的方向變成不是只有一種。像這個3D圖一樣一直下降找到山谷的最低點。所以叫梯度下降。
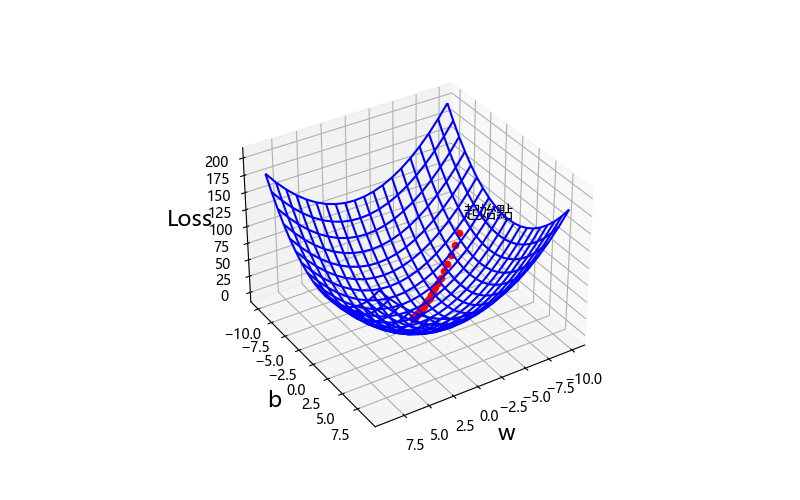
那怎麼求斜率呢?其實就是作函數的微分。
| 隨機森林 | 梯度提升 |
|---|---|
| 集成學習 | 集成學習 |
| 使用決策樹 | 使用決策樹 |
| 袋裝法(並列) | 提升法(順序) |
| 速度較快 | 速度較慢 |
| 精準度較低 | 精準度較高 |
| 不容易過擬合 | 容易過擬合 |
深度學習出現之前非常流行的方法。
基本思想是邊距(Margin)最大化。先來看一下下面這張圖,紅黃綠哪條分界線做分類比較好呢?
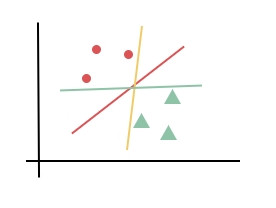
很明顯紅色的分界線比較好,因為它比較有餘裕,和資料點還有一段距離,用來預測未知資料時比較不會有錯誤分類的問題。所以支持向量機就是找到一個比較有餘裕的分界線,該分界線與每個資料點的距離最大。而離分界線最近的資料點叫支持向量(Support Vector)。如下圖所示。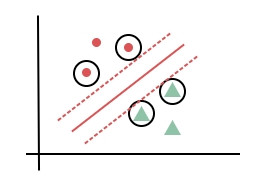
實際試著分類看看。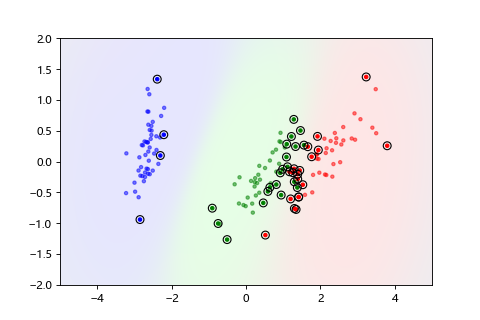
支持向量機之所以非常流行是因為可以處理無法線性分離的問題,使用 核函數(Kernel)將資料映射到更高的維度,達到線性分類的目的,同時可以透過核技巧(Kernel Trick)這個方法解決維度爆炸的問題。
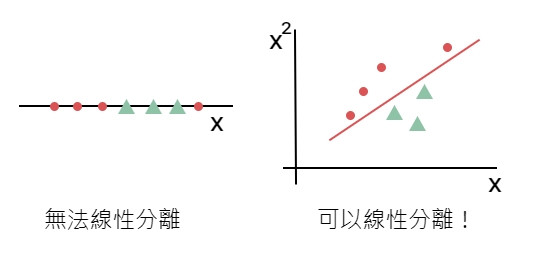
球都在桌子上無法用一條線做分類,用力拍桌子讓球通通浮在空中,就可以用一條空中的斜線做分類!
