今日大綱

• 什麼是線性判別分析?
• 線性判別分析 vs. 主成分分析 LDA vs. PCA
• 程式碼

什麼是線性判別分析?

線性判別分析為監督式學習的演算法，此方法與主成分分析一樣，用在處理資料降維時，讓模型避免發生維度災難的問題。目標為最小化組間內的變異，並且最大化組間的變異。

線性判別分析 vs. 主成分分析 LDA vs. PCA

• 線性判別分析為監督式學習方法，而主成分分析為非監督式學習。
• 線性判別分析目標為最小化投影後組間內的差異並且最大化投影後組間的差異，而主成分分析目標為最大化所有投影後資料之間的差異。兩個方法差別在於線性判別分析還有進一步考慮資料的類別，最小化同個類別資料之間的變異數。
• 假設目標變數維k個類別，線性判別分析特徵的維度最多只能降至k-1個維度，而主成分分析能夠降至任何一個維度。

程式碼

今天使用的程式碼一樣使用鳶尾花的資料集

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
## load the iris dataset
data = load_iris()

將x, y獨立出來

## extract the variables
x = pd.DataFrame(data['data'])
x.columns = data['feature_names']
y = data['target']

使用LDA降維，因為這個資料集的目標變數有3個類別，降為最多至2維，將n_components設為2

## the dimension of x is 4, and the dimension of y is 3. Therefore, we only can reduce the dimension to 2 (3-1).
lda = LinearDiscriminantAnalysis(n_components = 2)
lda_x = lda.fit_transform(x, y)

視覺化經過線性判別分析後的資料

## Visualize the transformed data
import matplotlib.pyplot as plt
plt.scatter(lda_x[:,0], lda_x[:,1], c = y)

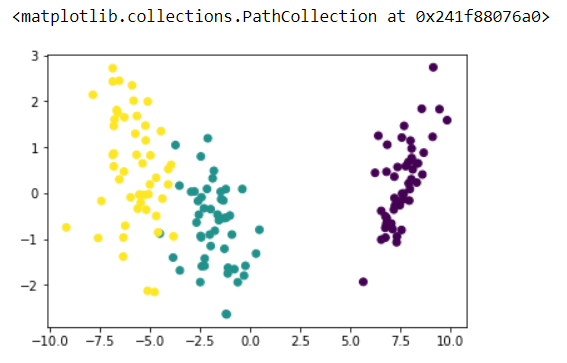
取得2個變數的貢獻率並且畫圖

ratio = lda.explained_variance_ratio_
np.set_printoptions(suppress = True)
print('各變數貢獻率: ', ratio)
plt.bar(['Variable 1' ,'Variable 2'], ratio)

程式碼已上傳至我的Github

參考資料

• Is LDA a dimensionality reduction technique or a classifier algorithm?
• 機器學習: 降維(Dimension Reduction)- 線性區別分析( Linear Discriminant Analysis)

感謝您的瀏覽，我們明天見!