圖片來源

線段是什麼？

點線面構成一切，而目前為止，我們都在花時間在點(Vector)跟面(Mesh)上。

線段由點產生，它也組成面，這之間需要轉換API。除此之外，還要透過多種的方法「繪製」線段，例如貝茲曲線、弧線、橢圓等等各式各樣，這也需要API。

佐為不碰棋也可以下棋。而你不用碰像素你也可以在像素中繪製形狀。你就像佐為一樣，指揮進藤光繪製你的畫面！

三個重要的線段物件：Shape、Path、Curve

1. Shape形狀，可以拿它的API畫畫。可以用來產生Mesh物體，如ShapeGeometry、ExtrueGeometry。
2. Path路徑：單純描述一條線，也可以用它的API畫畫。
3. Curve曲線：可以用它的API，產生幾何的曲線，例如橢圓形。

這三個就衍生很多東西：

1. 曲線可以變成線段嗎？可以——ShapePath
2. 線段可以變形狀嗎？可以——Shape
3. 線段可以變成點嗎？可以——.getPoints()
4. 曲線可以變成面嗎？可以——.getPoints()成為vector3之後建立Shape再建立ShapeGeometry
5. …

整個API主要就是關於線段的繪製，以及這三個東西的轉來轉去。我們先介紹繪製（Path跟Curve 為主），再介紹轉形。

線段物件：線Path

如果有用Canvas畫線，或是用P5.js畫線，那應該會對這個工具相當熟悉，因為Canvas跟P5.js也有用到類似的東西。如果對Canvas繪製有興趣可以看這裡，對P5.js有興趣可以看這裡。基本上three.js有Path就是在解決類似的事情。也就是畫線段。

這些繪畫的API概念是這樣的：

先想像你是棋靈王裡面的佐為。

圖片來源

你是一千年前精通Canvas畫線的鬼魂，在那年鐵人賽當中敗給某個日本Canvas大名，然後被封印起來。一千年後，你終於可以出來繪製Canvas了！然而你卻沒辦法碰到Canvas。

然後你碰到了叫「進藤three」的男孩，你必須透過進藤three才可以下棋。

圖片來源

如果你是佐為，你要怎麼告訴進藤three要怎麼下棋？

圖片來源

「13E」，你肯定是這樣說的。你佐為要把棋下在13E，而對進藤three來說，就是 Path.moveTo(13,E)

圖片來源

好的，接下來就用這個概念去思考以下的函式：

• 當前位置：Path.currentPoint

  這是變數。進藤three幫你作畫時會一直移動他的手指頭，手指頭叫做.currentPoint，預設在原點。

  

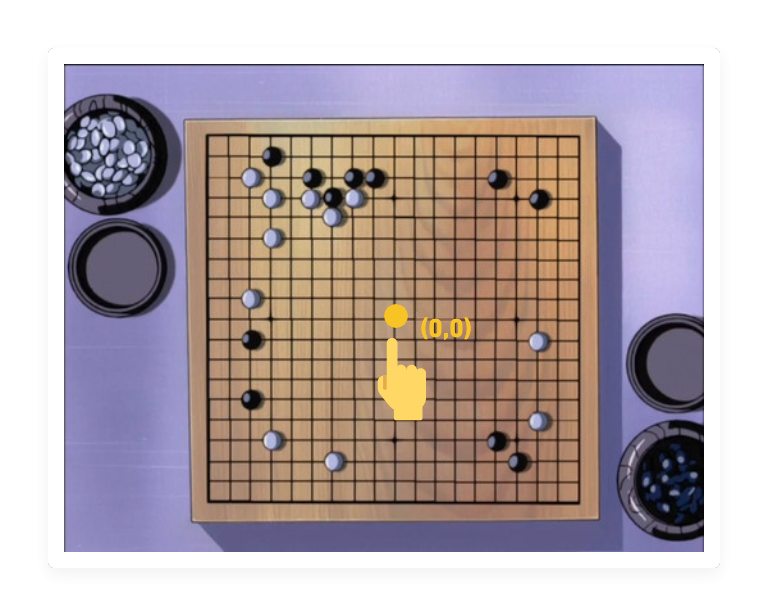
• 位移位置：Path.moveTo(x,y)

  「進藤three，移動你的手到(a,b)！」

  

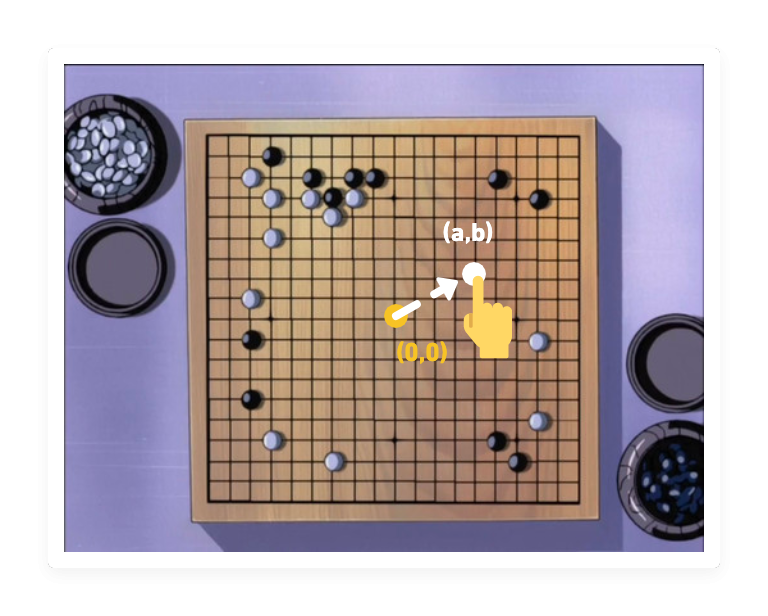
• 畫直線：Path.lineTo(j,k)

  「進藤three，現在畫直線到位置(j,k)！」

  

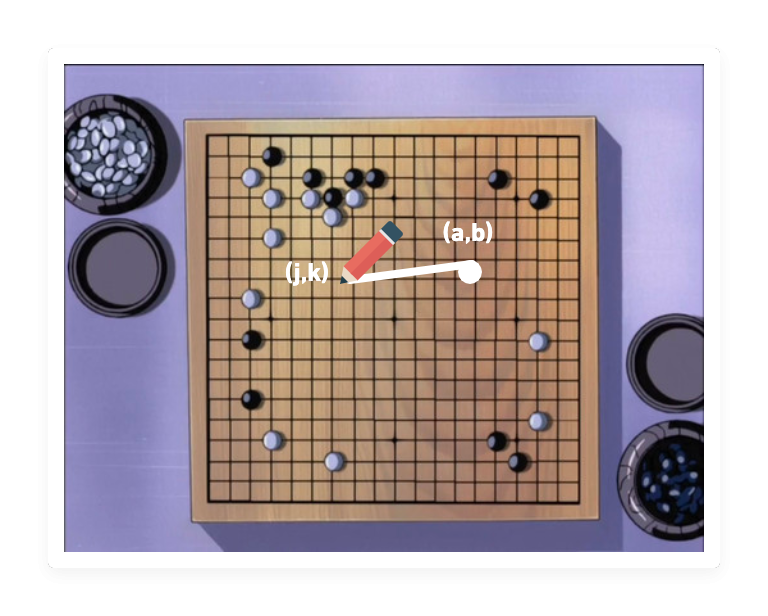
• 畫弧線：Path.arc(x, y, radius, aStartAngle, aEndAngle, aClockwise)

  「進藤three，現在以(x,y)為中心，以radius半徑，以aStartAngle為起始的弧度，以aEndAngle為結束的弧度，以aClockwise為繪製的方向預設以逆時針，繪製一個圓弧！」（進藤three要昏倒了）

  

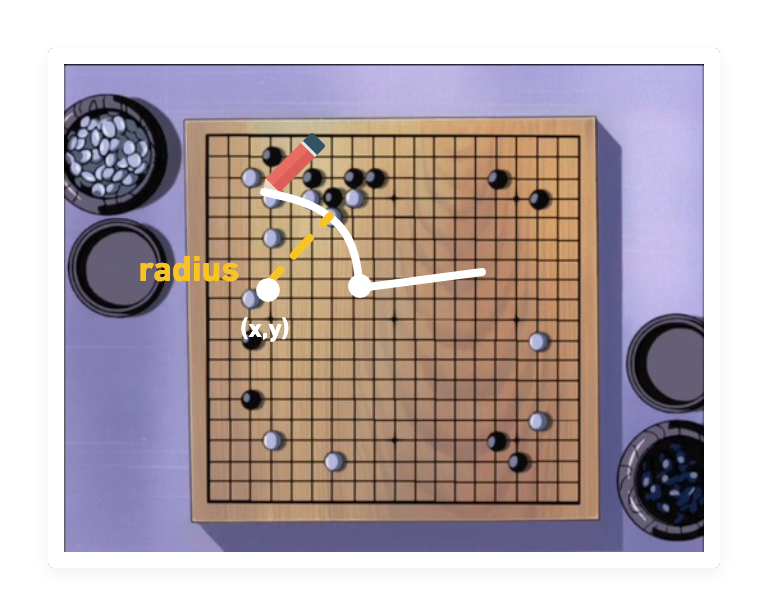
• 也是畫弧線：Path.absarc(x, y, radius, aStartAngle, aEndAngle, aClockwise)

  跟前一個Path.arc一模一樣，只是在名稱上多加了abs。abs是什麼呢？就是絕對值absolute的縮寫。意思是：原本相對於當前原點currentPoint 繪圖的弧線，變成以物件原點繪圖的弧線。

• 畫橢圓弧線：Path.ellipse(x, y, xRadius, yRadius, startAngle, endAngle, clockwise, rotation)

  「進藤three，跟Path.abs差不多，但這次是橢圓，所以有xRadous做為水平半徑，yRadius為垂直半徑，以rotation為偏移，繪製一個圓弧！」

  

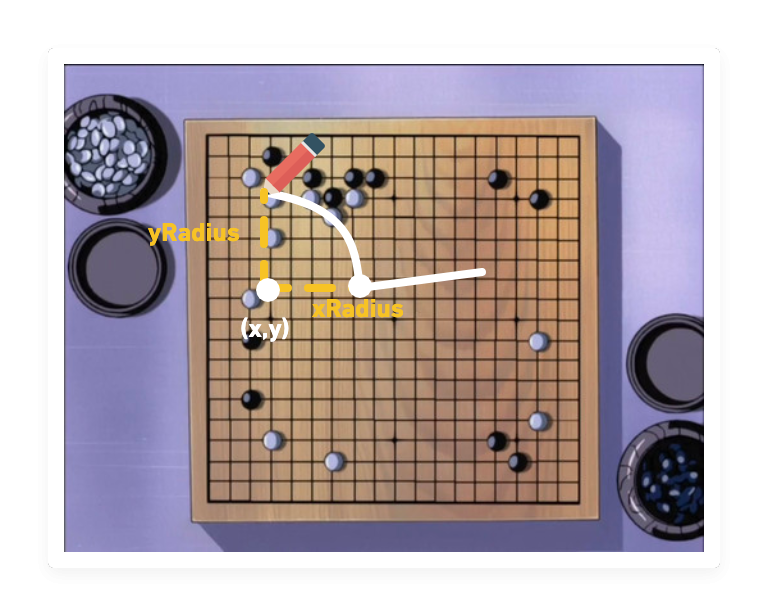
• 也是畫橢圓弧線：Path.absellipse(x, y, xRadius, yRadius, startAngle, endAngle, clockwise, rotation)

  跟前一個Path.ellipse一模一樣，只是多加了abs，意思就是：這裡繪製絕對位置，而不是跟上一個一樣以currentPoint 做為相對位置來畫線。

• 繪製貝茲曲線：Path.bezierCurveTo(v0, v1, v2, v3)

  「進藤three，以v0為第一個控制點，以v1為第二個控制點，以v2為目的地，繪製一條線段！」

  

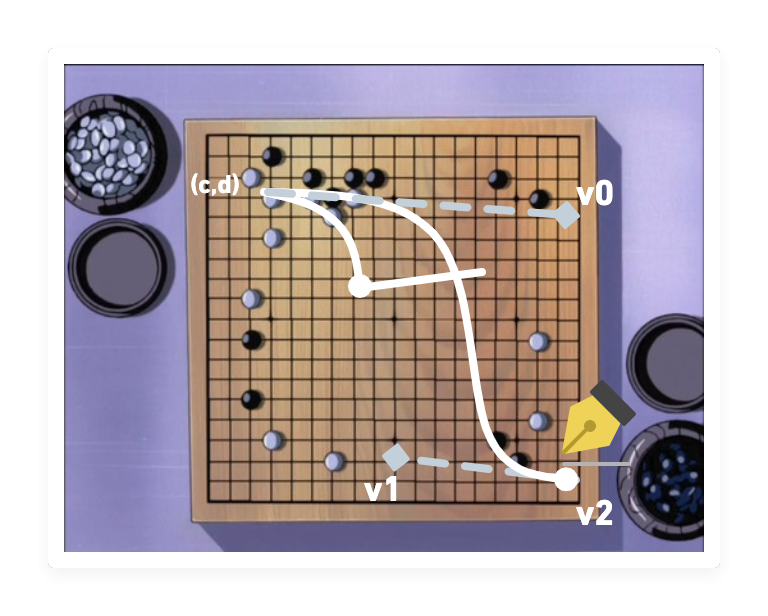
• 繪製二次方貝茲曲線：Path.quadraticCurveTo()

  「進藤three，以v0為第一個控制點，以v1為目的地，繪製一條線段！」

  

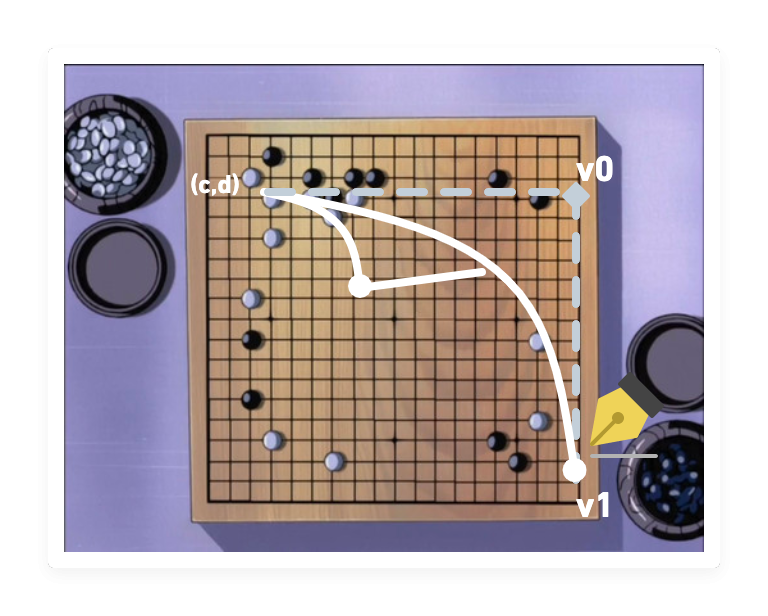
• .getPoint() / getPointAt()

  這個是用在一個線段取點。帶入點的位置，起點是0終點是1，就可以回傳一個錨點，代表該點的位置。

  參考資料：https://threejs.org/docs/?q=curve#api/en/extras/core/Curve

• .getPoints()

  在一個線段取多個點，帶入10就會回傳10個點代表0.1, 0.2, 0.3。回傳一組錨點

• setFromPoints()

  由一組點來產生線段。

線段物件：曲線Curve

上面提到的線，其實就有使用到曲線了。

事實上，當我們使用arc, absarc, ellipse, absellipse 時，就是將曲線加入到Path中。然而這只處理曲線部分的弧線而已。除了弧線以外，曲線還有很多API可以使用。

Three.js裡面Curve分很多種物件，包含

1. QuadraticBezierCurve ⇒ 二次貝茲曲線

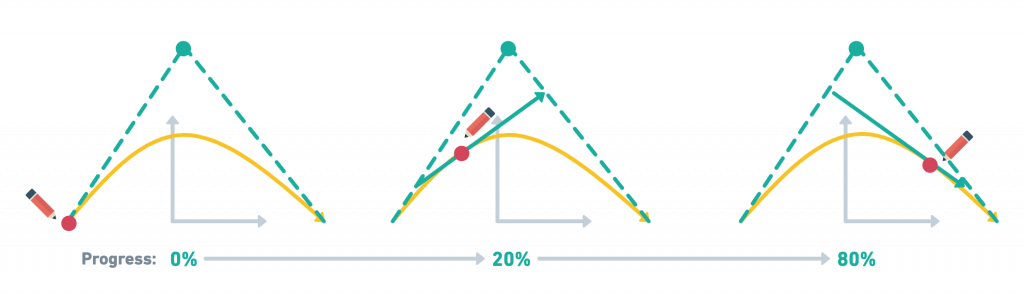
   • Quadratic有平方的意思。為一個控制點所形成的曲線。不僅在three.js，在SVG也常見。下圖可以見到與虛擬的控制點相連的兩條虛線，沿著進度繪製的話，可以繪製出曲線。

     

     

     圖片來源

   • 實例化方式

     const curve = new THREE.QuadraticBezierCurve(
     	new THREE.Vector2( 0, 0 ),
     	new THREE.Vector2( 30, 15 ),
     	new THREE.Vector2( 20, 0 )
     );
     

   • 相當於：

     

   • 相當於SVG的指令Q （取Quadratic首字）：

     <svg width="30" height="30" viewBox="0 0 30 30" fill="none" xmlns="http://www.w3.org/2000/svg">
     	<path d="M0,30 Q30,15 20,30" stroke="black"/>
     </svg>
     

2. CubicBezierCurve ⇒ 三次貝茲曲線

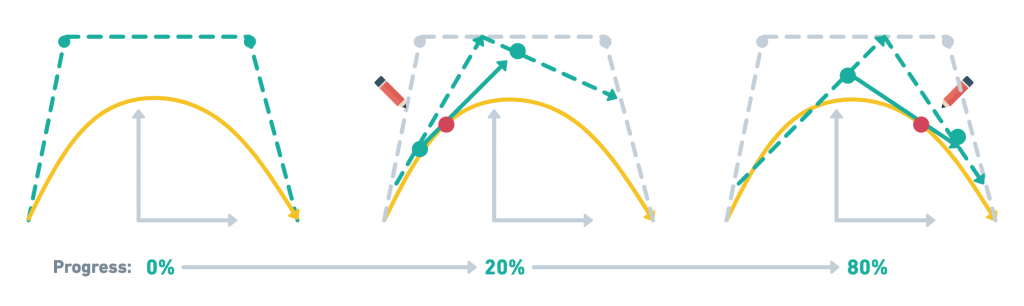
   • Cubic有代表三次元的意思。為一個控制點所形成的曲線。不僅在three.js，在SVG也常見。下圖可以見到與兩個虛擬的控制點相連的三條虛線，沿著進度繪製出兩條虛線，用那兩條虛線做二次貝茲曲線，可以繪製出曲線。

     

   • 實例化方式

     const curve = new THREE.CubicBezierCurve(
     	new THREE.Vector2( 0, 0 ),
     	new THREE.Vector2( 5, 15 ),
     	new THREE.Vector2( 30, 15 ),
     	new THREE.Vector2( 20, 0 )
     );
     

   • 相當於：

     

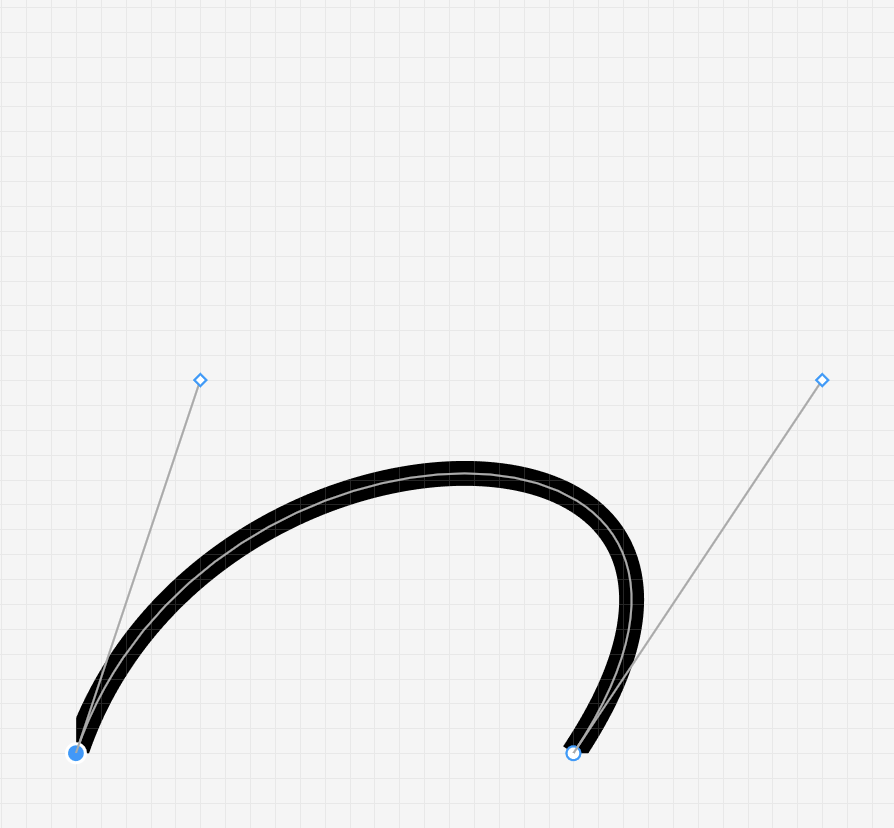
     這就等同於Illustrator的鋼筆工具（有兩個控制點時）的狀態：

     

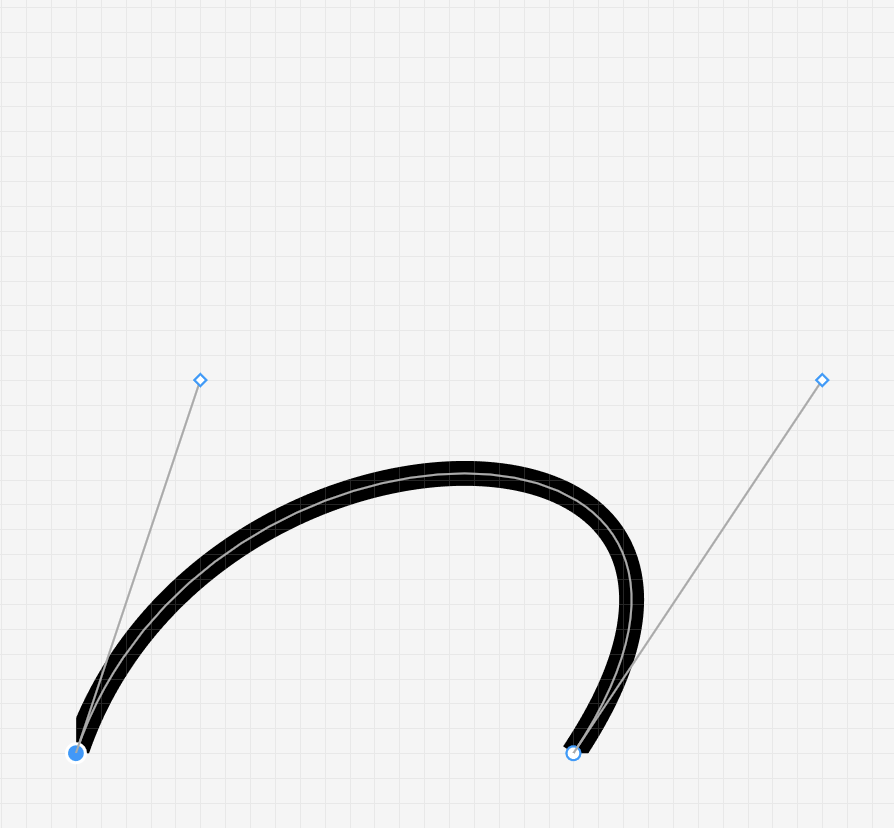
     等同figma的（有兩個控制點時的）線段工具：

     

   • 相當於SVG的指令C （取Cubic首字）：

     <svg width="30" height="30" viewBox="0 0 30 30" fill="none" xmlns="http://www.w3.org/2000/svg">
     <path d="M0,30 C5,15 30,15 20,30" stroke="black"/>
     </svg>
     

3. LineCurve ⇒ 直線，等同一次貝茲曲線

   • 實例化方式

     const curve = new THREE.LineCurve(
     	new THREE.Vector2( 0, 0 ),
     	new THREE.Vector2( 5, 15 ),
     );
     

   • 相當於：

     

   • 相當於SVG的指令L （取Line首字）：

     <svg width="30" height="30" viewBox="0 0 30 30" fill="none" xmlns="http://www.w3.org/2000/svg">
     <!-- 
         path標籤裡面有屬性d，d裡面有數字跟英文。英文就代表指令。這裡含有指令L。 
     -->
     <path d="M0,30 L5,15" stroke="black"/>
     </svg>
     

4. EllipseCurve ⇒ 橢圓弧線

   • 實例化方式

     const curve = new THREE.EllipseCurve(
     	10,  10,            // ax, aY
     	5, 3,           // xRadius, yRadius
     	0,  2 * Math.PI,  // aStartAngle, aEndAngle
     	false,            // aClockwise
     	0                 // aRotation
     );
     

   • 相當於：

     

   • 相當於SVG的ellipse ：

     <svg width="30" height="30" viewBox="0 0 30 30" fill="none" xmlns="http://www.w3.org/2000/svg">
     <path d="M0,30 L5,15" stroke="black"/>
     </svg>
     

5. ArcCurve ⇒ 弧線 ⇒ 即是EllipseCurve

6. CatmullRomCurve ⇒基於Catmull-Rom（樣條）而生成的曲線

7. SplineCurve

補充說明：貝茲曲線的前世今生？

在1912年，貝茲曲線的前身「伯恩斯坦多項式」由俄羅斯數學家謝爾蓋·納塔諾維奇·伯恩施坦提出，最早可不是貝茲本人提出呢！

圖片來源

直到1959年，為了發展省油的流線型汽車，汽車空氣力學的應用導入了歐洲的汽車工業中，物理學家兼數學家保羅（Paul de Casteljau at Citroen）成功將這個曲線導入到汽車的設計之中，可惜因為他所屬的公司雪鐵龍不允許他發表這個設計，使得事後導入曲線的雷諾汽車工程師貝茲先生Pierre Bezier成功申請專利，並且發揚光大。

直到1982年，貝茲曲線才出現在軟體產業。三位電腦工程師因為不滿提案被科技公司駁回，於是出走創業，透過研發PostScript並應用貝茲曲線，他們的公司得以出名，畢竟貝茲曲線是很新潮的概念，它使當時的字形跳脫了點陣圖思維，畢竟能讓文字無限縮放且不失真在當時是相當了不起的事情。

1985年，這家公司讓PostScript變成具有GUI的桌面軟體，貝茲曲線也在這時被廣泛應用在設計與軟體開發中，而這個軟體正是illustrator。這家公司的名字其實就是Adobe。

圖片來源

補充說明：貝茲曲線的核心概念

概念很簡單，我們先從直線說起：

從直線說起

假裝我們是縫紉機好了，縫紉機有一個「車針」會隨著時間前行，縫出（繪製出）一條直線。

假設時間是0~1，縫紉機車針位置為L，走了一條直線由P0到P1，我們假設P0跟P1都是平面上的一個二維向量，則移動的公式為：

// t: 時間，0≤t≤1
// P0:起點二維向量
// P1:終點二維向量
L = P0+(P1-P0)*t
// 展開變成：
L = (1-t) * P0 + t * P1

可以用下面的圖說來呈現其過程：

圖片來源

如果看不懂的話，我拆解公式：

1. 你可以先想像P0是原點(0,0)，那麼L就是(P1-P0)*t 。(P1-P0) 代表兩點之間的線段向量。就如同下圖：

   

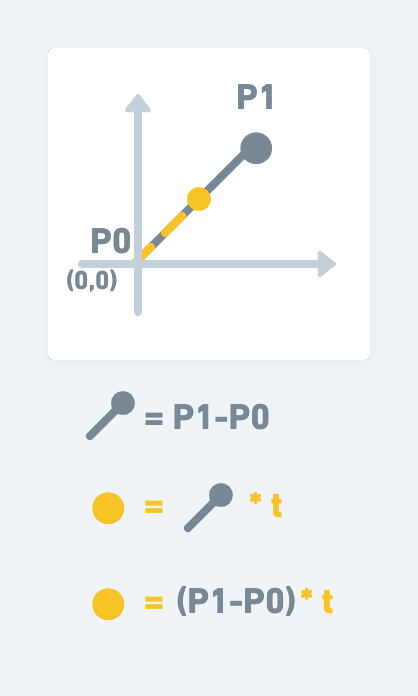
2. 現在思考：實際上P0不一定位於原點(0,0)，有可能在他處，所以P0必須當起點，也因此公式上必須再加上P0 + 才行，就像下圖：

   

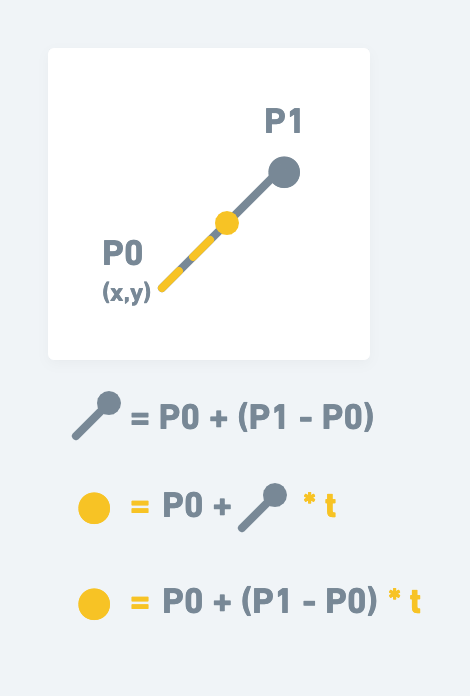
3. 公式可以展開，變成：

   

以上是直線的車針移動過程。我們透過以上概念，延伸到二次方貝茲曲線上：

二次貝茲曲線

// t: 時間，0≤t≤1
// P0:
// P1:
// P2:二次貝茲的線段終點
// 黃點: 直線邏輯時從P0到P1所得出的車針位置
// 綠點: 比照黃點，直線邏輯時從P1到P2所得出的車針位置
// 紫點: 二次貝茲曲線時在P0,P1,P2所得出的車針位置，以下解釋
黃點 = (1-t) * P0 + t * P1
綠點 = (1-t) * P1 + t * P2
Q = (1-t) * 黃點 + t * 綠點

1. 假設我們有三個點：P0, P1, P2，二次貝茲曲線至少要有三個點。

   

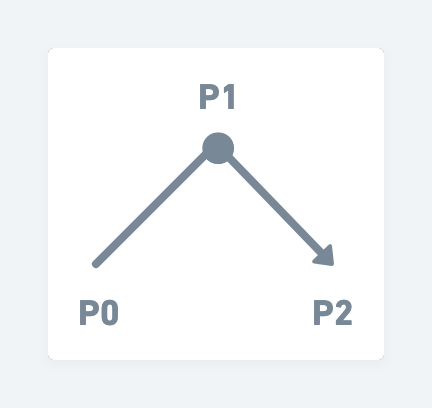
2. 我們從剛才推導的直線概念，得知了黃色的點位置，以及綠色的點位置。

   

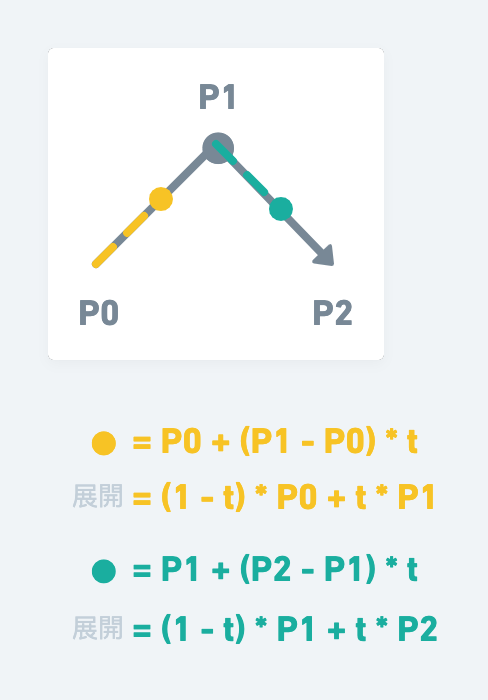
3. 現在我們建立一條直線（藍線），由黃點到綠點的直線，也就是綠點減黃點的向量

   

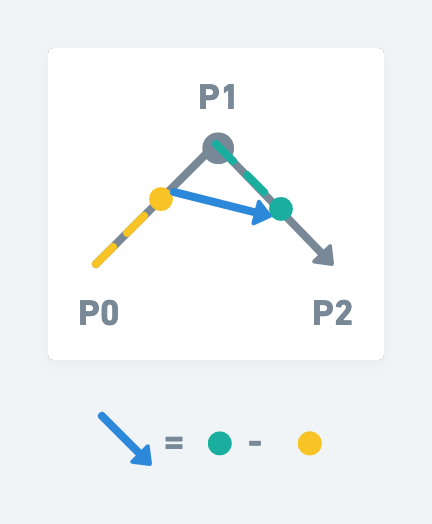
4. 如果結合前兩步驟，就可以得到藍線的向量

   

5. 在藍線上，我們用同樣的時間t 帶入到藍線上的位置，則紫色的點就是「車針」要走的位置

   

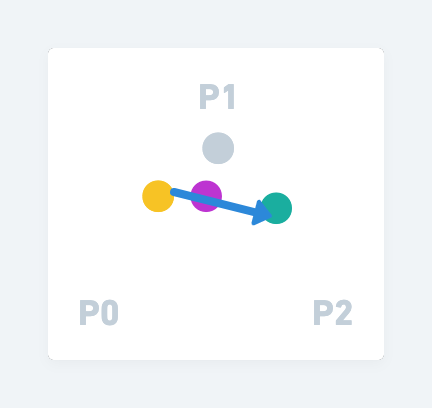
6. 這個車針位置怎麼取得呢？
   我們回想一下在最一開始討輪直線時，我們運用的公式：

   黃點 = P0+(P1-P0)*t
   

   這個公式中，線段中的起點P0跟終點P1可得出黃色的點。而今我們要得出紫色的點，只要把黃點跟綠點視作直線中P0跟P1般存在，就可求得。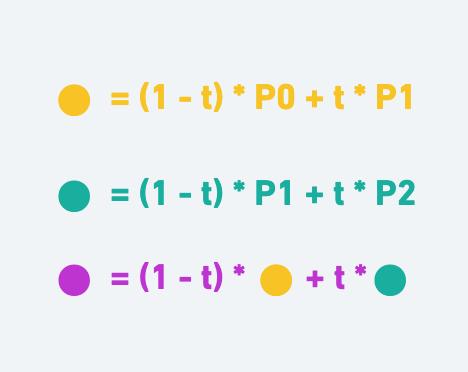
   

7. 於是，車針就可以走完線段，完成二次方貝茲曲線

   

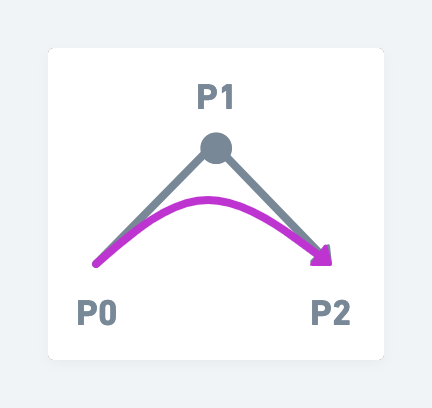
三次貝茲曲線

三次貝茲曲線，可以想成：以上同樣的邏輯，操作三次。

// t: 時間，0≤t≤1
// P0
// P1
// P2
// P3
// 黃點: 直線邏輯時從P0到P1所得出的車針位置
// 綠點: 比照黃點，直線邏輯時從P1到P2所得出的車針位置
// 灰點: 比照黃點，直線邏輯時從P1到P2所得出的車針位置
// 紫點: 二次貝茲曲線時在P0,P1,P2所得出的車針位置
// 棕點: 比照紫點的邏輯，二次貝茲曲線在P1,P2,P3所得出的車針位置
// 紅點: 三次貝茲曲線在P0,P1,P2,P3所得出的車針位置，下面解釋
黃點 = (1-t) * P0 + t * P1
綠點 = (1-t) * P1 + t * P2
灰點 = (1-t) * P2 + t * P3
紫點 = (1-t) * 黃點 + t * 綠點
棕點 = (1-t) * 綠點 + t * 灰點
紅點 = (1-t) * 紫點 + t * 棕點

1. 三次貝茲曲線至少要有四個點

   

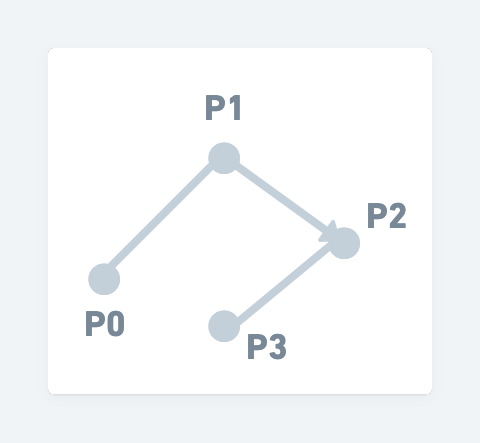
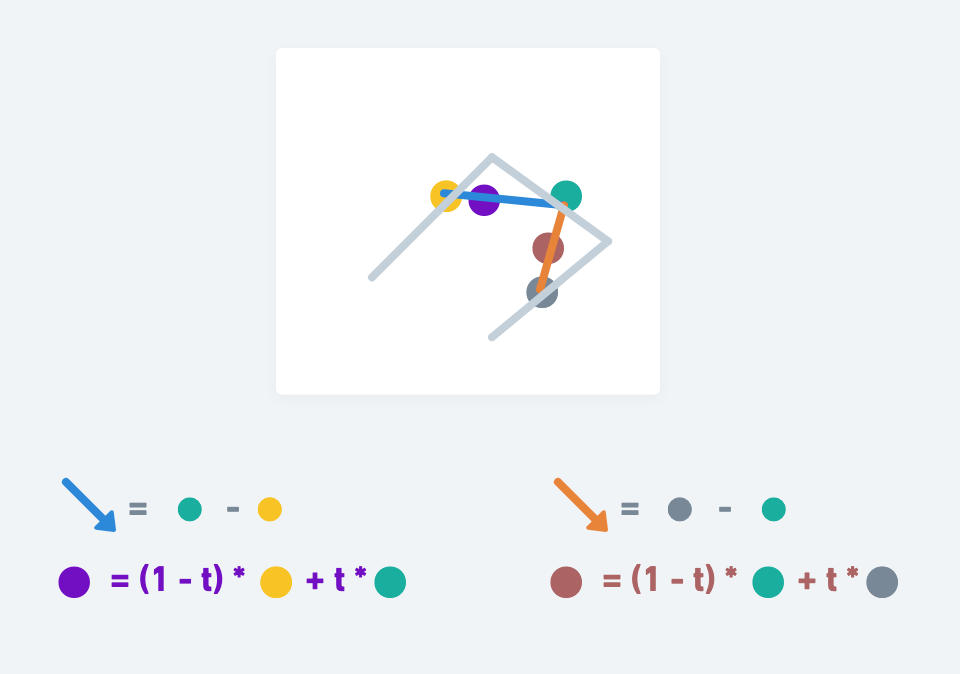
2. 沿用二次貝茲曲線的邏輯，我們可以找出兩條直線：藍線跟橘線，以及找到紫色點跟棕色點

   

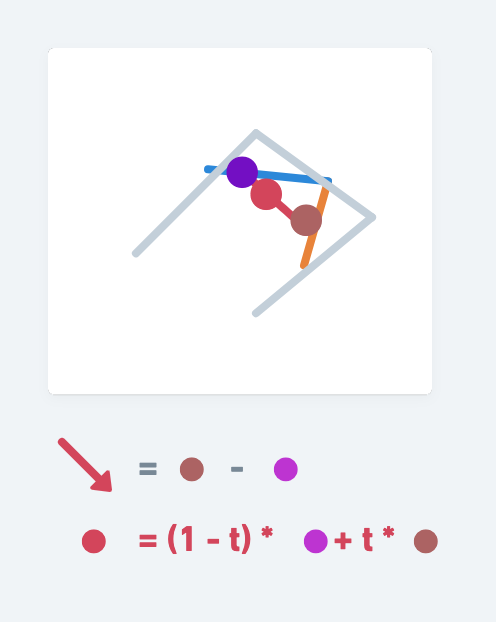
3. 在這個架構下，再疊加一層同樣的邏輯，就可以取得紅線以及紅點。紅點就代表車針的位置。

   

由此，我們就可以透過公式認識二次、三次的貝茲曲線。

我需要精通這些東西嗎？

如果要設計線條，才需要精通線段。我們如果生在一個Illustrator剛出來的年代，貝茲曲線可說是當紅炸子雞，潮到像是Web3一樣新穎。

但時間到了現代，如果真的要設計線條，可以直接在Figma, Adobe Illustrator上面設計即可。對於2D線段來說，還有更多更有趣函式庫可以運用，例如P5.js。

除非線段是raw data產生的，不然用其他工具繪製即可。那如果線段是raw data呢？那在開發時會更注重物件之間的轉換。例如：將SVG經由線段轉換成面。

轉換物件對應用來說相當重要

所以說，我們不用精通線段，只要能夠拿來應用即可。但麻煩的是，當我們要轉換線段物件時，容易被搞得很複雜。下圖是我製作的關係圖，可供參考有關線段的物件之間的關係。有了這張表對我自己的幫助很大：

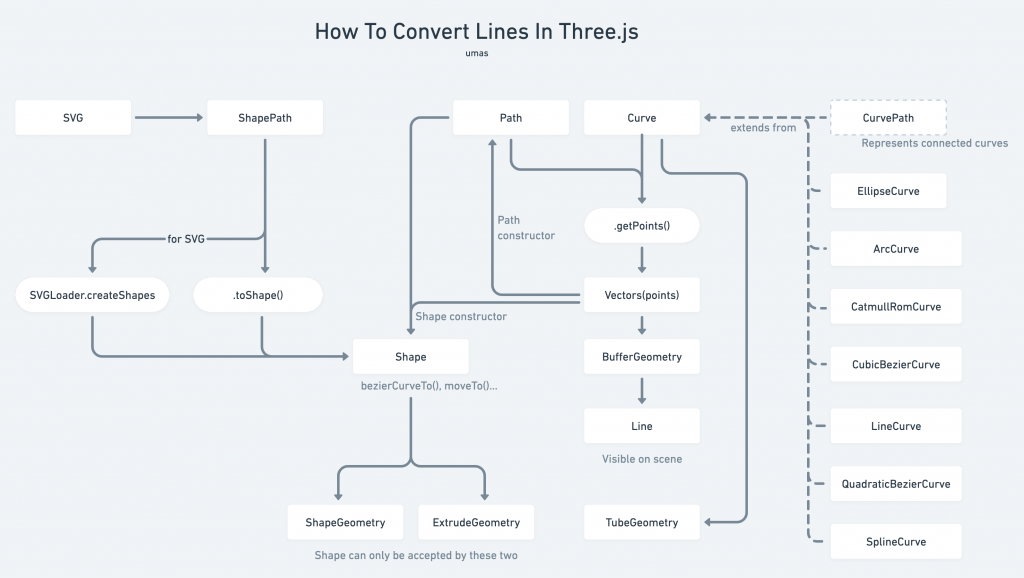
以這張圖表我們就可以很清楚的看到Three.js 各種元件的轉換關係。

比如說，如果我要從SVG匯入線段資料，並且製作成面，那該怎麼辦？

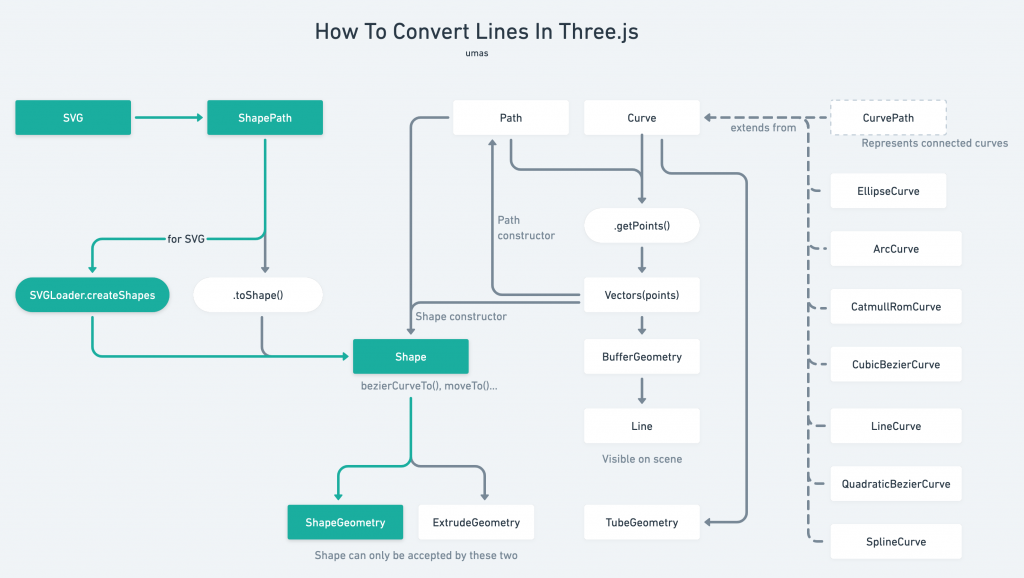
走這個轉換的路線即可。

那麼如果說要把流體力學的三維錨點資料轉成線段該怎麼處理呢？

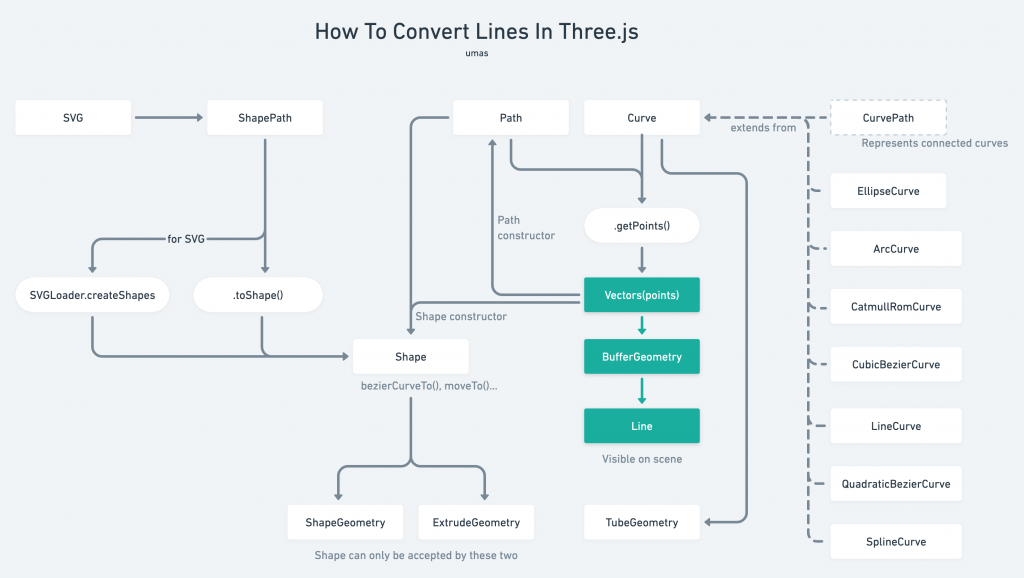
將點轉成Line物件即可。

那麼如果要在場景中的地球加上一個拋物線以相連兩座城市呢？

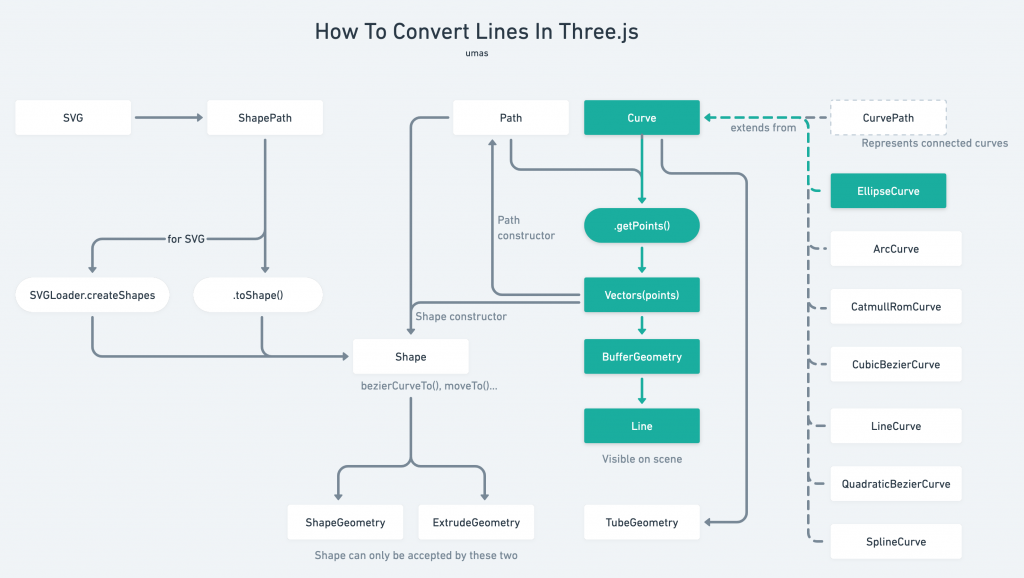
製作一個曲線，再轉成點，再轉成線即可。

線段的工作流程

從上面的圖可以理解：通常工程師通常不用自己畫線，我們只要使用某個原始資料（rawdata）的線段，然後呈現在畫面上就好。舉例來說：

1. 將SVG的線段繪製成面，SVG為rawdata
2. 將流體力學的計算結果（例如火災的二氧化碳飄逸情況）以線段呈現方向
3. 用戶在3D場景選擇建築物的起訖點，網頁得找到最佳路徑，並以線段標記路徑
4. 將定時回傳的飛機位置資訊連成線段，呈現在地球上
5. 場景有地球，地球有兩個座標要用拋物線相連
6. 火車模型得沿著軌道移動，其軌道為資料庫物抓來的一組(x,y)資料。
7. 給定高架橋的橫切面還有高架橋的路徑，工程師用這兩個資料製作3D高架橋

下篇

我將實戰線段。使用線段去產生3D的圓餅圖。圖表跟線段關聯很大，如果要製作一個數位中控台儀表板，圖表是不可或缺的元素，而圓餅圖不僅是常見的圖表，將其做成3D也能夠讓畫面更為絢麗、獨有。使得產品能在競爭對手之間脫穎而出。

結語：塔矢亮看完這篇一定感到震驚。

圖片來源

好好當sai就好了當three幹嘛

圖片來源

參考資料

一次搞懂SVG中的d屬性中的指令

Paths

d

EllipseCurve

貝茲曲線公式