筆者決定用以下三點結論規劃接下來的實作：

結論一：決定不用機器學習處理目前的資料

1. 資料量太少，僅百餘筆，訓練可能導致 overfitting 等問題。
2. 任何事情別急著想用 AI 解決，用其他的方式或許可以更快、更有效達成我們期待的效果。

結論二：決定使用平均數作為預測基準

戴久永教授現代統計學的發展
一文提到：「對於集中趨勢的測度。最早的集中趨勢的測度實際上可追溯至古希臘，是算術平均數......對大多數的目的而言算術平均數是最常用的集中趨勢測度，這當然有它學理上的意義。」

而在林嘉澍教授迴歸分析的三個基本概念一文中，認為可以用平均值來作為預測以及將來預測的比較基準：「我們想像一下最簡單的迴歸公式，其實就是一直線! 比方我要預測期末可成績，就用Y=85這個全班平均值來預測即可。當然，我們想要做更精密的預測，所以引入了X變項(出席時間)，看看加入個別出席時間這個變項以後，得到的預測值會不會比Y=85來得更好。」

這句話給了我當頭棒喝，仔細想想其實我們問題的本質並不複雜！雖然用平均數作為預測結果或許會導致一些誤差（例如他們最近兩個月可能因為人員流動，導致將來三個月內每個人都會晚 10 分鐘下班），但這些優化都是後事，讓我們先取得一個參考基準作為 POC (Proof of concept)。

根據「迴歸分析的三個基本概念」，我們可以有兩種模式來預測：

1. 模式A：不考慮X變項的影響，直接用一個常數來預測Y值。所以對每個一個Xi，預測的結果永遠都是Y。
2. 模式B：考慮X變項的影響，除了常數以外，再根據每一個X來預測Y (Y=bX+a)。

在此我們使用模式A，亦即針對每一個同樣的星期幾，都使用一樣算術平均數來作出預測。

將來若要設計其他的預測模型，我們可以用平均數作為比較的基準。例如，我們最初的需求是十分鐘前發出通知提醒要關門了，所以假設今天預測值提前了五分鐘，那麼這五分鐘便可以特別記錄，思考是什麼因素造成誤差，如季節、溫度等。

所以我們也需要一併記錄後續的誤差以及其他可能的影響因素。在沒有更好的點子之前，我們後續的記錄除了維持 Day 07 提到的「小時分鐘+日期+星期幾+備註」以外，至少還要加入預測時間以及實際關門時間的欄位。

結論三：將預測時間切割為上午及下午時段分別預測

讓我們再看一次昨天生成的散佈圖：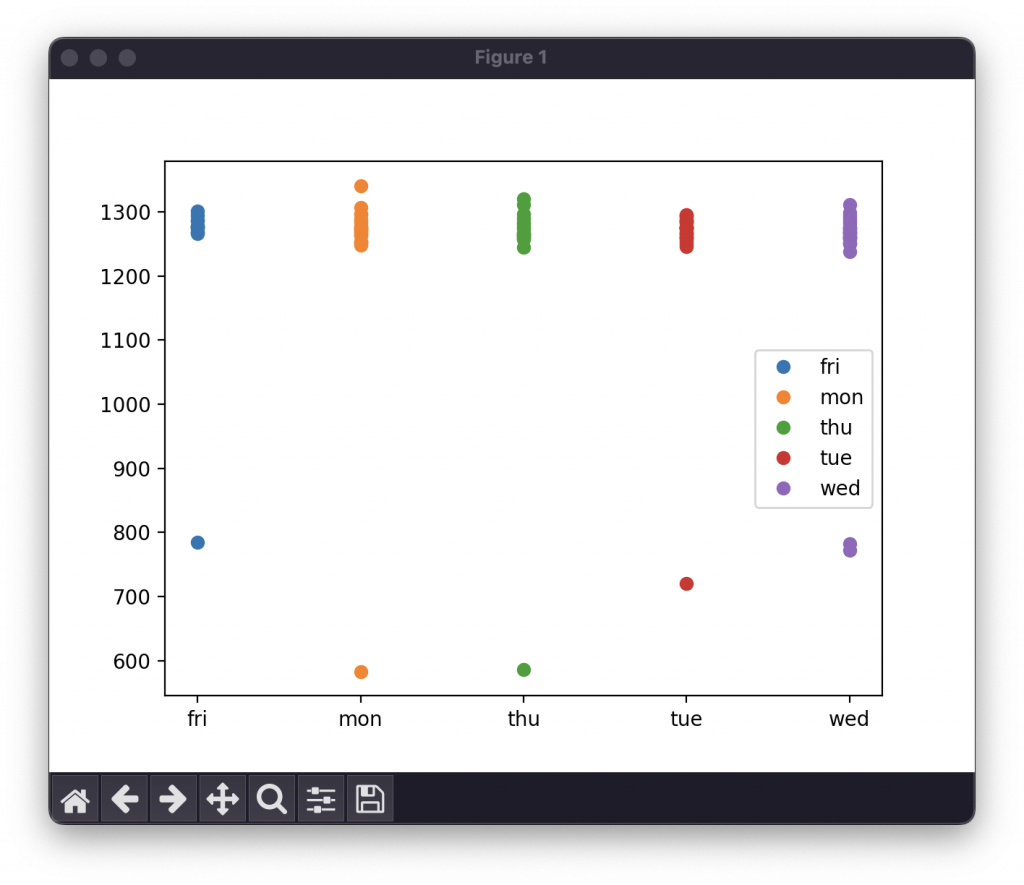

1. 早上關門的筆數明顯比晚上來得還要少很多。
2. 需要解決週六以及週日沒有任何記錄的問題。

筆者決定試圖用以下兩點來解決我們碰到的困境：

1. 週六、週日一併適用週五的預測值：因為該店三天工作量大致相等（參照 Day 19 的觀察），我們先用週五的預測值當作週六以及週日的預測值。待後續有記錄後，再來觀察校準。
2. 早上關門的時間統一處理：早上的筆數太少，但仍需要預測，故我們將五天的早上時間統一加總，計算平均數作為每一天的早上時間預測。透過後續記錄，再來校準誤差。

明天讓我們開始實作。

今天收工！

延伸閱讀

• 所需資料量：10 倍法則
• How much data is required for machine learning?
• 數據分析POC的三大原則