有限狀態機

維基百科中有一段有限狀態機的定義

有限狀態機（英語：finite-state machine，縮寫：FSM）又稱有限狀態自動機（英語：finite-state automaton，縮寫：FSA），簡稱狀態機，是表示有限個狀態以及在這些狀態之間的轉移和動作等行為的數學計算模型。

也許大家不清楚有限狀態機的用途，但是我們應該對於循序電路有一定了解，因此我會用「計數器」來解釋狀態機。

大家不妨再次想想計數器怎麼有辦法從非初始狀態開始運作？最主要的原因是，計數器的電路包含記憶元件，因此我們可以知道上一步運行的結果。記憶元件，以過往的例子就是正反器(flip-flop)。

狀態也許有點抽象，但是你不妨視他為可能的結果。舉例來說，一個 mod-9 計數器，共包含 9 種狀態，分別是 0, 1, 2, ..., 8。這些就是所謂的「有限個狀態」。

另一個重點是「狀態之間的轉移」，同樣是 mod-9 計數器，我們假設當前的狀態是 7 ，如果此時我們接收到的輸入是 1 ，那是不是代表我們的狀態會被轉移至 8 。這其實就是循序電路的核心概念，下一個狀態是根據前一個狀態和輸入來決定的，因此同樣都是狀態 7 ，當接收的輸入是 0 ，也許可以將下一個狀態設定為 6 。

狀態轉移圖表

狀態與輸入的關係，除了可以條列式地列出來，另一種表示方式是使用狀態轉移圖表 (State-transition table)，大致的樣貌如下圖 (圖片來源：維基百科)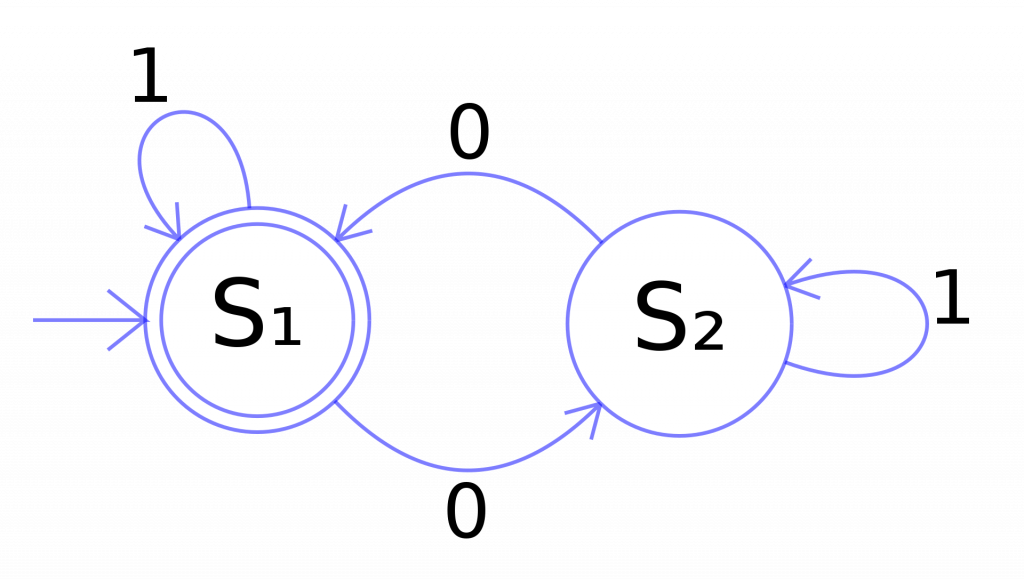

從這種圖表中，你可以很清楚的了解到各個狀態之間是怎麼轉移的，例如上圖有提到 S1 如果搭配輸入 1 ，可以將狀態變為 S2 ，反之如果搭配輸入 0 ，狀態仍舊維持 S2 。

要特別注意的是，狀態的切換時機是在「時脈正緣」的瞬間，因為在 Verilog 的程式碼中，我們通常是以

always @ (posedge clk) begin
    // some statements
end

來觸發正反器的運作，因此你可以理所當然的將狀態的切換時機定在「時脈正緣」！