在不同領域對於名詞的使用略有差異,不過指的都是同一件事,所以這邊稍微統整一下。
| 名詞 | 數學符號 | 圖例 |
|---|---|---|
| 節點Node, Vertex |  |
|
| 邊、連結、關係Edge, Link, Connection, Relation |  |
|
| 圖、網路Graph, Network |  |
|
| 社群Cluster, Community |  |
在 Network Science 中,有兩種最基本的圖,分別是『無向圖』以及『有向圖』。
| 無向圖Undirected Graph | 有向圖Directed Graph | |
|---|---|---|
| 定義 | 連接線無方向性,也可以視為雙向 | 每條邊有特定方向 |
| 範例 | 社交網路中的友誼關係,友誼是雙向的,沒有明確的起點或終點 | 飛機航線,每條航線有出發地和目的地,具有明確的方向 |
| 圖例 |  |
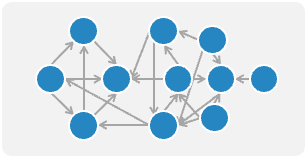 |
在進階一點又分為 binary 或是 weighted graphs
| 二元圖Binary Graph | 加權圖Weighted Graph | |
|---|---|---|
| 定義 | 邊只有兩種狀態,存在(1)或是不存在(0) | 每條邊都帶有一個額外的權重,像是這條邊的成本、距離等 |
| 範例 | 像是社群網路圖,認識就是(1);不認識就是(0,通常直接不畫出來)下面的圖只是一個範例,通常就直接省略不畫出來 | 假設節點是城市,邊的權重就是城市跟城市之間的實際距離 |
| 圖例 | 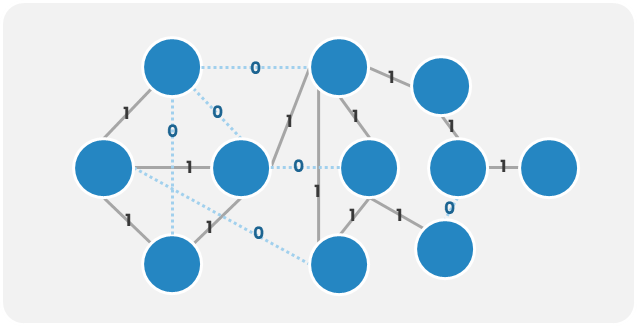 |
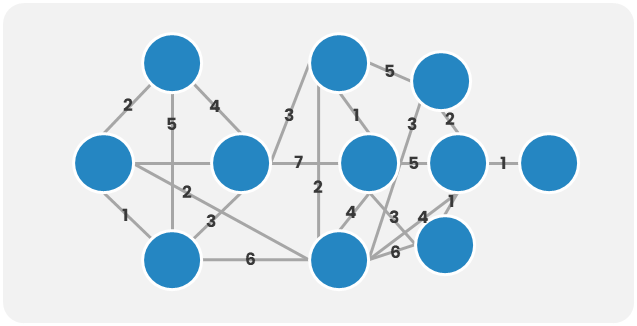 |
如果以節點來看,有有分成 homogeneous/heterogeneous graphs
| 同質圖Homogeneous Graph | 異質圖Heterogeneous Graph | |
|---|---|---|
| 定義 | 所有節點和邊都屬於同一種類型,彼此之間沒有區別 | 節點/邊擁有多種類型,有些人會稱呼這種圖為『知識圖譜』 |
| 範例 | 例如班級內的互動網路圖,只顯示每個人之間的互動關係。節點都是人;邊都是互動 | 例如下圖中每個節點的屬性就不相同名詞(碩士、論文、貓)、姓名(皮皮、小咪、牛奶)、形容詞(可愛)、地點(台科)等... |
| 圖例 | 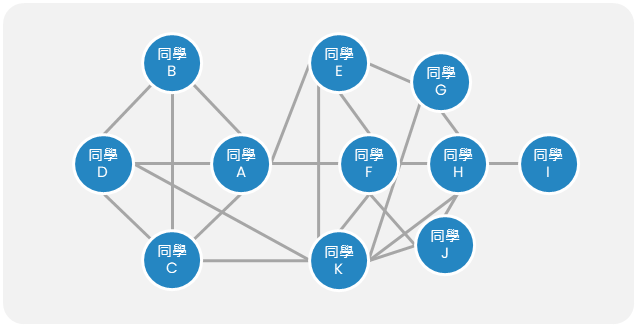 |
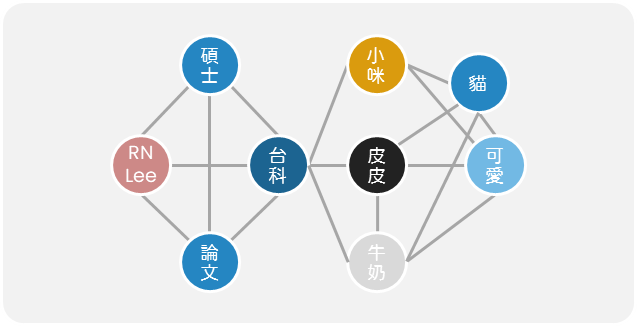 |
雖然我稱呼它們是特殊類型的圖,但其實下面者幾種圖更符合現實生活中的狀況
| 類型 | 特色 | 圖例 |
|---|---|---|
| Multigraphs | 兩個節點之間擁有多條邊,這些邊可能有相同或不同的屬性 | 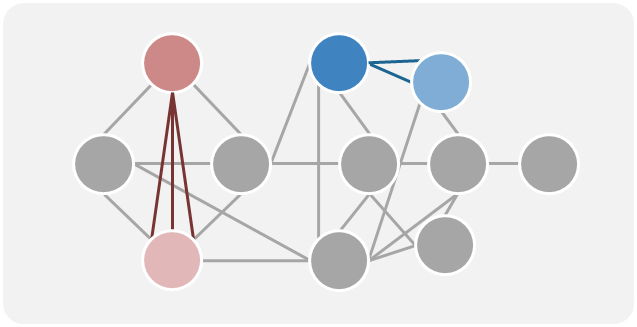 |
| Self-loop | 節點與自己之間存在一條環狀邊 | 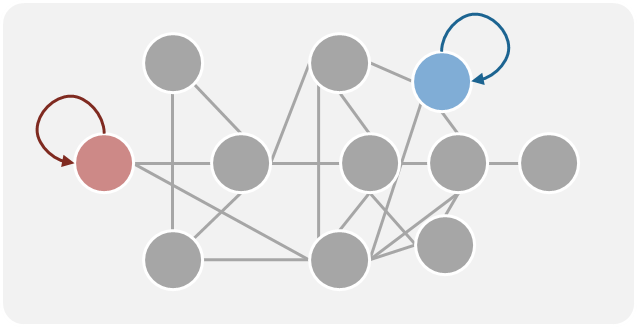 |
| Hypergraph | 在 Hypergraph(超圖)中,一條邊可以連接多個節點,稱為 Hyperedge(超邊)。這種圖補足了一般圖中只能顯示節點之間有連接的關係,可以額外顯示出這些節點是『同時』連接在一起的。有些人會用框起來的方式表達這些節點是同時發生;也有人用方形(事件)來把節點連在一起 | 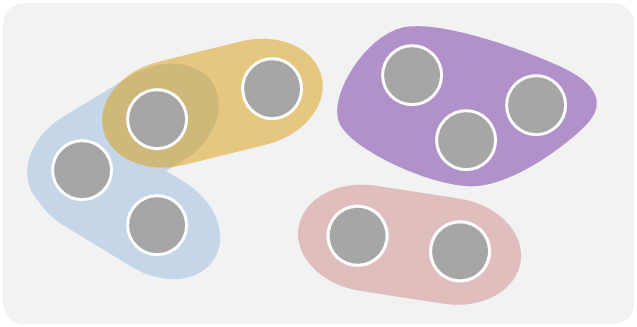 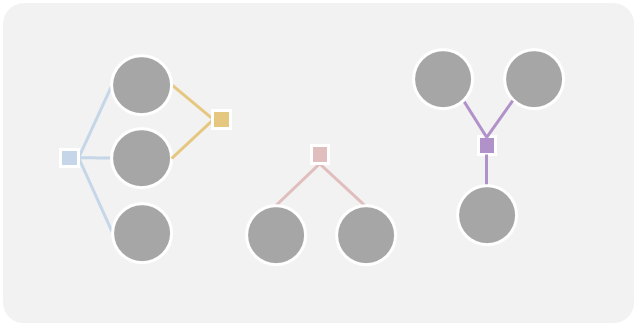 |
| Dynamic Graph | 與一般的靜態圖不同的點在於,它可以隨著時間的推移而變化,意思是指圖中的節點和邊可以隨時間添加、刪除或更改屬性 | 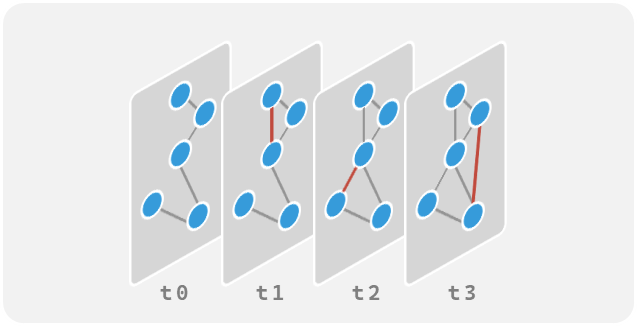 |
