一、 介紹

本次主題會探討影像處理中最重要的概念，如何以數學方式來表示影像，並詳細介紹摺積（Convolution）的原理。這一概念的重要性體現在它在影像處理中的廣泛應用，可用於實現平滑、銳化、邊緣檢測等各種操作。同時，摺積也是深度學習中卷積神經網路（CNN）的核心操作之一。因此，可以說，如果你不熟悉摺積，那麼你就不太可能理解影像處理的精髓。因此看到很多數學式正要跳出去的你，請你留下來！這個真的很重要！

二、 原理

1. 影像的數學表式

影像的數學表達方式使用函數f(x,y) 表示影像在座標 (x,y)處的像素值。在這個表示法中，x 和 y分別代表影像的水平和垂直座標位置，而 f(x,y) 則代表了這個位置的像素強度或顏色值。這種函數表示法讓我們能夠用數學的方式描述影像中每個位置的像素資訊，並且可以應用數學和影像處理技術來分析、處理和修改影像。

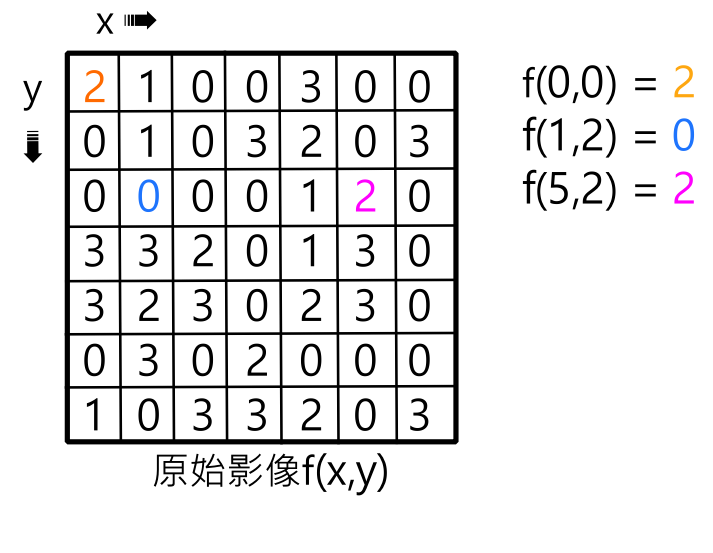
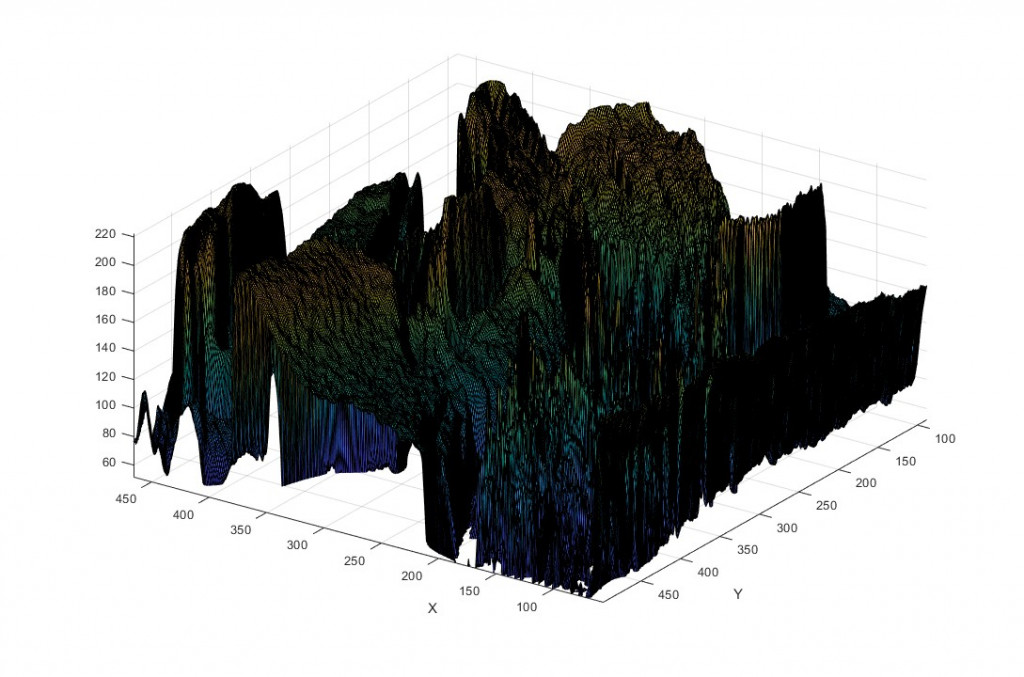
一張數位影像可以也可以使用3D的方式表達f(x, y)，其中：

• x 和 y 是影像上的座標，代表影像的行和列。這些座標指示了影像中的特定位置。
• f(x, y) 是在位置 (x, y) 上的像素值或顏色值。這個函數表示了該位置的亮度、顏色或灰階值。

我們可以將影像看作是一個立體的表面，每個點的高度（像素值）決定了該點的顯示效果。這種3D表示方法可以將影像的每個像素視為一個座標點，並將像素值（或顏色值）作為這個點在座標點的高度。

2. 核(Kernel)

在影像處理中，核（Kernel）有多種別名，這些別名的使用取決於具體的應用。常見的別名包括濾波器（Filter）、卷積核（Convolution Kernel）、權重矩陣（Weight Matrix）、形態學元素（Structuring Element）、鄰域（Neighborhood）等。這些名稱用於描述核在不同操作中的不同用途，但它們都指的是一個小型矩陣或陣列，用於對影像進行運算。

下面的圖片展示了一個3x3大小的核函數w(x,y) 的例子。在這個核函數中，w(x,y) 是核的中心，我們稱它為這個核的錨點(Anchor Point)。其他矩陣元素的位置是相對於核的錨點而定的。

3. 相關性和摺積運算

1) 相關性(Correlation)

有一個1x3大小的核w(x,y)和一個3x3大小的影像f(x,y)。我們將核w(1,2)也就是數字2，對準影像的f(0,0)也就是字母a，將重疊的元素相乘並相加，然後依序使用w(1,2)對f(x,y)的每個元素對齊並做運算，輸出的影像被定義為g(x,y)，這些運算稱為相關性。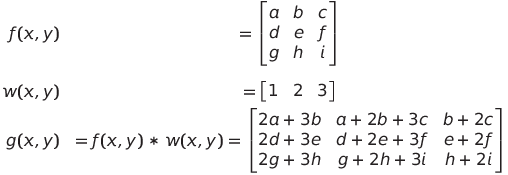

相關性運算在數學定義如下：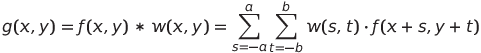

• a：核在x方向的大小除以2，使用無條件捨去忽略小數點，以上面的例子a=1。
• b：核在y方向的大小除以2，使用無條件捨去忽略小數點，以上面的例子b=0。
• w(x,y)：核函數。
• f(x,y)：輸入影像函數。
• g(x,y)：輸出影像函數。

以上的例子中，f(x,y)僅是一個3x3大小的影像，而且核函數是一維的。然而，實際上影像通常具有512x512甚至更大的尺寸，而且二維的核函數也經常出現在影像處理，比前面的例子更複雜，因此我們需要舉一個更大的例子。

1. 假設w(x,y)的所有元素都是1，大小為3x3。
2. 將核心對準在f(x,y)的左上角f(0,0)位置，然後將核心的每個數值與該位置及其鄰近的8個像素的像素值進行相乘。
3. 將這些相乘的結果加總在一起，得到輸出影像的左上角像素值。
4. 將核心向右移動一個像素到f(1,0)，再對新位置處的核心和像素值進行相關性運算，得到輸出影像的第二列像素值。
5. 重複步驟4，直到將核心在水平方向上完整掃過整張照片的第一行。
6. 將核心向下移動一個像素到f(0,1)，再從步驟2開始，對新位置處的核心和像素值進行相關性運算，直到將核心在垂直方向上完整掃過整張照片。
7. 當核w(x,y)到達右下角後，即完成相關性運算，得到一張新的輸出影像g(x,y)。

2) 摺積(Convolution)

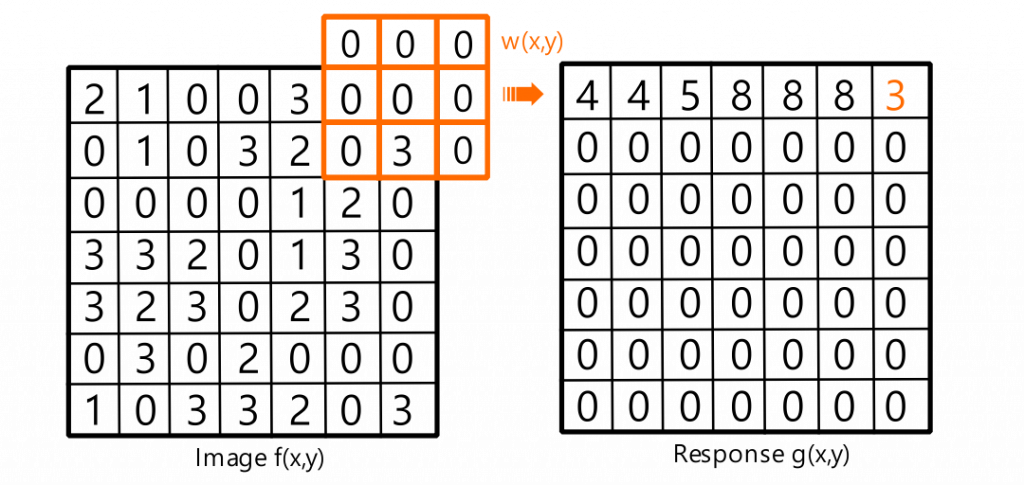
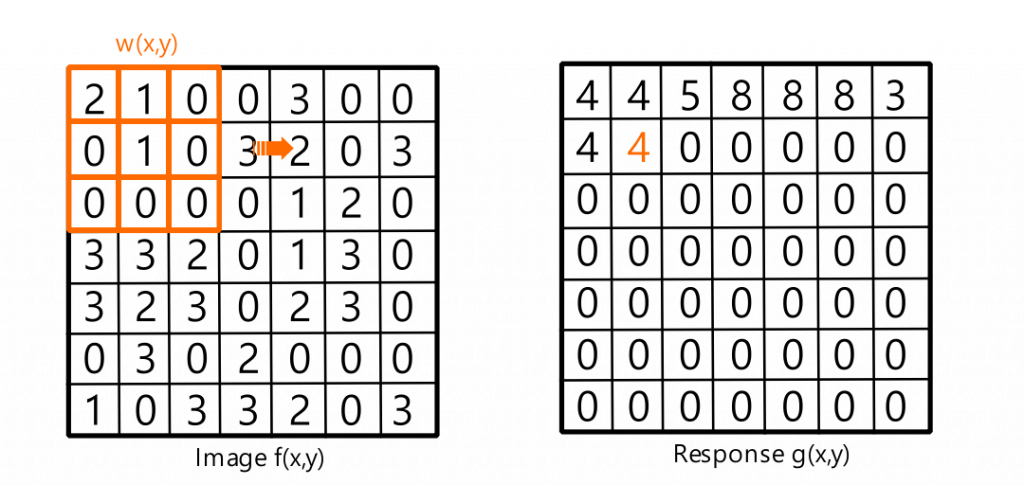
觀察下方的例子，你會發現只要將核旋轉180度在進行相關性運算，就是摺積運算。無論是摺積運算還是相關性運算，都會將核滑動到影像上的每個位置，並將核和影像的對應元素進行相乘並相加。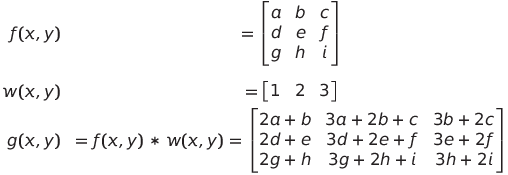

摺積在數學定義如下：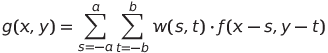

3) 觀念釐清? 相關性? 摺積? 空間濾波到底用哪個運算?

以下是我個人的見解，如有錯誤，歡迎指正。

儘管從數學角度來看，空間濾波器的操作看似使用相關性運算，但在實際的應用和教學中，常常被視為摺積運算。這是因為在許多影像處理的應用中，核函數是對稱的(但並非全部，如Sobel)，將其旋轉180度後仍保持相同的性質。

因此，在核函數對稱的情況下，相關性運算可以等效於摺積運算。另外，摺積運算在訊號處理領域是一個常見且常用的數學運算，對於有訊號處理基礎的人來說，使用摺積運算表示會更加直觀。

接下來的內容將會使用以摺積來代稱相關性的運算，因為這樣比較好理解。