一、介紹

離散傅立葉轉換（Discrete Fourier Transform，簡稱DFT）是一種信號處理技術，用於將時域（或空間域）中的離散數據序列轉換成頻域中的頻譜表示。DFT可視為將信號分解為不同頻率成分的過程。它在許多領域中都有廣泛的應用，包括影像處理、音訊處理、通信、數據壓縮等。

我們之前的主題都集中在空間域中進行核函數的摺積，並分析這種在空間域中的摺積效果。然而，使用核函數對影像進行空間域摺積是一個相對較慢的過程，而轉向頻域處理則可以使運算效率更高，且可以透過頻譜分析影像的特性。

二、原理

1. 離散傅立葉轉換(Discrete Fourier Transform)

一維的離散傅立葉轉換數學定義如下：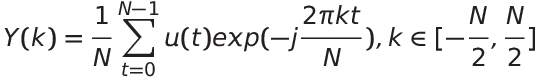

其中：

• k：頻率變數，值必須在-N/2到N/2的範圍內，超過這個範圍的頻率會出現混疊(Aliasing)。
• u(t)：輸入訊號。
• N：取樣總數。

舉個例子，假設有一個**f(t)**函數，包含了兩個頻率的正弦波1Hz和3Hz，其函數為：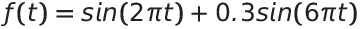

我們可以看到這個函數在時域上的波形。

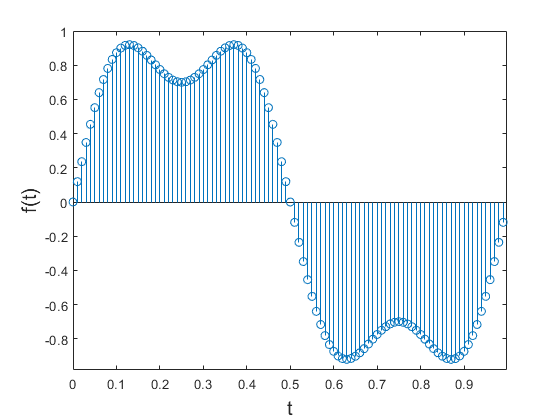
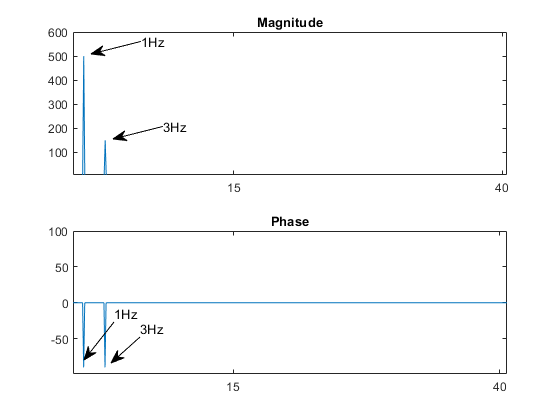
接著我們對這個函數做傅立葉轉換，可以得到下圖在1Hz和3Hz出現脈衝，這代表這個函數是由一個振幅較大的1Hz正弦波以及振幅較小的3Hz正弦波組成。正好驗證了我們上面函數的特性。藉此，我們可以透過DFT分析離散訊號在頻域上的特性。

由於我們的圖片是離散的二維訊號f(x,y)，無法使用上述的公式做轉換。因此，我們需要使用二維的離散傅立葉轉換，對影像做DFT。

二維的離散傅立葉轉換數學定義如下：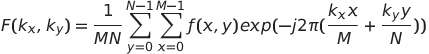

其中：

• kx、ky：X、Y座標個別頻率。
• M：影像的寬度(width)。
• N：影像的高度(height)。

三、程式碼

1. 逐行解釋

1) 最佳化影像大小

傅立葉轉換通常要求輸入的長、寬是2、3、5的次方。這樣的數字可以讓 DFT 的效率更高。使用 cv::getOptimalDFTSize()可以獲得取得最佳化長、寬大小。並使用cv::copyMakeBorder將輸入影像的邊界向外延伸，延伸的深度即為最佳化大小減去原影像大小。

cv::Mat padded; 
// 將輸入影像擴展至最佳大小
int n = cv::getOptimalDFTSize(I.rows);
int m = cv::getOptimalDFTSize(I.cols);
// 在邊界上添加零值，以確保影像大小為偶數
copyMakeBorder(I, padded, 0, n - I.rows, 0, m - I.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));

2) 使用OpenCV進行離散傅立葉轉換

將延伸過後的輸入影像和一個大小相同且元素全為0的矩陣合併成一個雙通道的影像。並使用cv::dft()對這張影像做傅立葉，要注意輸入的影像必須是CV_32F、CV_64F。

// 將影像轉換為複數格式，用於DFT計算
cv::Mat input_channels[] = {cv::Mat_<float>(padded), cv::Mat::zeros(padded.size(), CV_32F)};
cv::Mat input;
cv::merge(input_channels, 2, input); // 將兩個平面合併成一個複數影像

// 執行離散傅立葉變換（DFT）
cv::Mat complexI;
cv::dft(input, complexI);

3) 計算複數平面振幅

由於傅立葉係數的動態範圍太大，無法顯示。造成高值全部顯示為白點，而低值全部顯示為黑點。如果要使用灰階圖顯示頻譜，必須將線性標度轉換為對數標度，其數學公式如下：

// 分離複數影像的實部和虛部
cv::split(complexI, dft_result); 
//使用實部和虛部計算大小
cv::magnitude(dft_result[0], dft_result[1], magnitude);
cv::Mat magI = magnitude + cv::Scalar::all(1);
cv::log(magI, magI);

• cv::magnitude()：對頻譜的實數、虛數部分取歐氏距離。
• cv::log()：對影像的每一個元素取對數。

4) 剪裁頻譜並重新排列傅立葉象限

接下來將第一步擴展的影像裁切掉。為了讓頻譜可視化，我們可以重新排列結果的象限，以便原點(0,0)與影像中心相對應。

• 左上與右下象限交換
• 右上與左下象限交換。

// 裁剪頻譜以適應偶數大小
magI = magI(cv::Rect(0, 0, magI.cols & -2, magI.rows & -2));
// 重新排列傅立葉變換的象限，使原點位於影像中心
int cx = magI.cols / 2;
int cy = magI.rows / 2;
cv::Mat q0(magI, cv::Rect(0, 0, cx, cy)); // 左上 - 建立象限區域
cv::Mat q1(magI, cv::Rect(cx, 0, cx, cy)); // 右上
cv::Mat q2(magI, cv::Rect(0, cy, cx, cy)); // 左下
cv::Mat q3(magI, cv::Rect(cx, cy, cx, cy)); // 右下
cv::Mat tmp; // 交換象限（左上和右下）
q0.copyTo(tmp);
q3.copyTo(q0);
tmp.copyTo(q3);
q1.copyTo(tmp); // 交換象限（右上和左下）
q2.copyTo(q1);
tmp.copyTo(q2);

2. 完整程式碼

#include <iostream>
#include "opencv2/opencv.hpp"
#include "opencv2/core/utils/logger.hpp"

using namespace std;

int main()
{
    // 設定 OpenCV 日誌等級為 SILENT，以抑制除錯訊息
    cv::utils::logging::setLogLevel(cv::utils::logging::LOG_LEVEL_SILENT);

    // 讀取灰階影像 Lenna.png，如果無法讀取則輸出錯誤並退出
    cv::Mat I = cv::imread("C:\\Users\\vince\\Downloads\\Lenna.png", cv::IMREAD_GRAYSCALE);
    if (I.empty()) {
        cout << "Error opening image" << endl;
        return EXIT_FAILURE;
    }
	cv::Mat padded; 
    // 將輸入影像擴展至最佳大小
    int n = cv::getOptimalDFTSize(I.rows);
    int m = cv::getOptimalDFTSize(I.cols);
    // 在邊界上添加零值，以確保影像大小為偶數
    copyMakeBorder(I, padded, 0, n - I.rows, 0, m - I.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));

    // 將影像轉換為複數格式，用於DFT計算
    cv::Mat input_channels[] = {cv::Mat_<float>(padded), cv::Mat::zeros(padded.size(), CV_32F)};
    cv::Mat input;
    cv::merge(input_channels, 2, input); // 將兩個平面合併成一個複數影像

    // 執行離散傅立葉變換（DFT）
    cv::Mat complexI;
    cv::dft(input, complexI);

    // 計算傅立葉變換的振幅，並轉換為對數尺度
    cv::Mat dft_result[2];
    cv::Mat magnitude;
    // 分離複數影像的實部和虛部
    cv::split(complexI, dft_result); 
    //使用實部和虛部計算大小
    cv::magnitude(dft_result[0], dft_result[1], magnitude);

    // 轉換為對數尺度
    cv::Mat magI = magnitude + cv::Scalar::all(1);
    cv::log(magI, magI);

    // 裁剪頻譜以適應偶數大小
    magI = magI(cv::Rect(0, 0, magI.cols & -2, magI.rows & -2));

    // 重新排列傅立葉變換的象限，使原點位於影像中心
    int cx = magI.cols / 2;
    int cy = magI.rows / 2;
    cv::Mat q0(magI, cv::Rect(0, 0, cx, cy)); // 左上 - 建立象限區域
    cv::Mat q1(magI, cv::Rect(cx, 0, cx, cy)); // 右上
    cv::Mat q2(magI, cv::Rect(0, cy, cx, cy)); // 左下
    cv::Mat q3(magI, cv::Rect(cx, cy, cx, cy)); // 右下
    cv::Mat tmp; // 交換象限（左上和右下）
    q0.copyTo(tmp);
    q3.copyTo(q0);
    tmp.copyTo(q3);
    q1.copyTo(tmp); // 交換象限（右上和左下）
    q2.copyTo(q1);
    tmp.copyTo(q2);

    // 正規化至 [0, 1]
    normalize(magI, magI, 0, 1, cv::NORM_MINMAX);

    // 顯示原始灰階影像
    cv::imshow("Input Image", I);

    // 如果輸入影像為浮點數，影像會自動乘以 255 並顯示
    cv::imshow("Spectrum Magnitude", magI);
    cv::waitKey();
    return EXIT_SUCCESS;
}

3. 輸出結果

經過離散傅立葉轉換後，我可以得到下圖的結果，右邊即為影像f(x,y)的頻譜。

四、參考資料

• OpenCV：Discrete Fourier Transform