一、介紹

在上一個章節，我們學習了如何使用離散傅立葉轉換來生成頻譜。然而，離散傅立葉轉換還有另一個極其重要的應用。我們可以透過信號處理中的摺積定理，將影像轉換為頻域，並在頻域中進行元素相乘運算，同時避免了繁瑣的空間域中的摺積運算，提高影像處理的效率。

二、原理

1. 摺積定理

摺積定理是信號處理中的一個基本原理。當我們對一個函數f(x,y)和另一個函數g(x,y)進行摺積運算，然後對其結果進行傅立葉轉換，我們會得到這兩個函數在頻域中的相乘結果。我們可以將空間域中的濾波操作轉換為頻域中的相乘運算。

摺積定理的數學定義如下：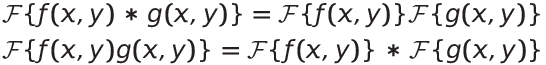

其中：

• f(x,y)：原始影像。
• g(x,y)：核函數。

三、程式碼

1. 逐行解釋

1) 選擇核函數

可以使用 FILTER 選擇要使用平均濾波或是高斯濾波，分別觀察不同的輸出效果。

#define FILTER_MEAM 0
#define FILTER_GAUSSIAN 1
#define FILTER FILTER_GAUSSIAN

2) 初始化核函數

1. 使用 cv::getOptimalDFTSize 函數計算最佳的傅立葉變換大小，並將大小儲存於dft_rows、dft_cols。
2. 建立一個空白的 cv::Mat 矩陣 dft_kernel，用於存儲核函數在傅立葉域表示，並將其初始化為零矩陣。
3. 建立一個子矩陣 dft_kernel_part，其大小與核函數 kernel 相同。
4. 通過 convertTo 函數將核函數 kernel 複製到dft_kernel_part。
5. 進行傅立葉變換，結果儲存於dft_kernel。

void init_kernel(cv::Size image_size,cv::Mat kernel) {
    dft_rows = cv::getOptimalDFTSize(image_size.height + kernel.rows - 1);
    dft_cols = cv::getOptimalDFTSize(image_size.width  + kernel.cols - 1);
	dft_kernel = cv::Mat::zeros(dft_rows,dft_cols,CV_32F);
    cv::Mat dft_kernel_part = dft_kernel(cv::Rect(0, 0, kernel.cols, kernel.rows));
    kernel.convertTo(dft_kernel_part, dft_kernel_part.type(), 1, 0);
    cv::dft(dft_kernel, dft_kernel,0, kernel.rows);
}

3) 在頻域上的摺積操作

1. 建立一個名為 dft_image 的空白矩陣，用於存儲 DFT 結果。
2. 建立一個子矩陣 dft_image_part，其大小等於輸入影像的大小。
3. 預處理輸入影像，將其轉換為單精度浮點數數據類型並確保平均值為零。
4. 執行離散傅立葉變換（DFT）操作，將影像轉換為頻域表示。
5. 將 DFT 影像與預先計算的 DFT 核函數進行逐元素相乘，實現摺積操作。
6. 執行逆離散傅立葉變換（IDFT）操作，將頻域結果轉換回空間域，同時進行剪裁。

cv::Mat convolute_on_frequency_domain(cv::Mat image){
    cv::Mat dft_image = cv::Mat::zeros(dft_rows,dft_cols,CV_32F);
    cv::Mat dft_image_part = dft_image(cv::Rect(0, 0, image.cols, image.rows));
    
    image.convertTo(dft_image_part, dft_image_part.type(), 1,-cv::mean(image)[0]);

    cv::dft(dft_image, dft_image,0,image.rows);

    cv::mulSpectrums(dft_image, dft_kernel, dft_image, 0, true);
    cv::idft(dft_image, dft_image, cv::DFT_SCALE, image.rows + kernel.rows - 1);
    cv::Mat corr = dft_image(cv::Rect(0, 0, image.cols + kernel.cols - 1, image.rows + kernel.rows - 1));
    return corr;
}

2. 完整程式碼

#include <iostream>
#include "opencv2/opencv.hpp"
#include <chrono>
#include "opencv2/core/utils/logger.hpp"
#define FILTER_MEAM 0
#define FILTER_GAUSSIAN 1
#define FILTER FILTER_GAUSSIAN      

using namespace std;
cv::Mat kernel;
cv::Mat dft_kernel;
int dft_rows;
int dft_cols;

cv::Mat convolute_on_frequency_domain(cv::Mat image){
    cv::Mat dft_image = cv::Mat::zeros(dft_rows,dft_cols,CV_32F);
    cv::Mat dft_image_part = dft_image(cv::Rect(0, 0, image.cols, image.rows));
    
    image.convertTo(dft_image_part, dft_image_part.type(), 1,-cv::mean(image)[0]);

    cv::dft(dft_image, dft_image,0,image.rows);

    cv::mulSpectrums(dft_image, dft_kernel, dft_image, 0, true);
    cv::idft(dft_image, dft_image, cv::DFT_SCALE, image.rows + kernel.rows - 1);
    cv::Mat corr = dft_image(cv::Rect(0, 0, image.cols + kernel.cols - 1, image.rows + kernel.rows - 1));
    return corr;
}

void init_kernel(cv::Size image_size,cv::Mat kernel) {
    dft_rows = cv::getOptimalDFTSize(image_size.height + kernel.rows - 1);
    dft_cols = cv::getOptimalDFTSize(image_size.width  + kernel.cols - 1);
	dft_kernel = cv::Mat::zeros(dft_rows,dft_cols,CV_32F);
    cv::Mat dft_kernel_part = dft_kernel(cv::Rect(0, 0, kernel.cols, kernel.rows));
    kernel.convertTo(dft_kernel_part, dft_kernel_part.type(), 1, 0);
    cv::dft(dft_kernel, dft_kernel,0, kernel.rows);
}
int main() {
    cv::utils::logging::setLogLevel(cv::utils::logging::LOG_LEVEL_SILENT);

    // 讀取灰度影像
    cv::Mat image = cv::imread("C:\\Users\\vince\\Downloads\\Lenna.png", cv::IMREAD_GRAYSCALE);

    cv::Mat kernel;
#if FILTER==FILTER_MEAM 
    kernel = cv::Mat::ones(cv::Size(21, 21), CV_32FC1);
    kernel /= kernel.rows*kernel.cols;
#endif

#if FILTER==FILTER_GAUSSIAN
    cv::Mat x_kernel=cv::getGaussianKernel(21, 4);
    cv::Mat y_kernel=cv::getGaussianKernel(21, 4);
    cv::transpose(y_kernel, y_kernel);
    kernel = x_kernel * y_kernel;
#endif

    init_kernel(image.size(),kernel);

	auto t1 = std::chrono::high_resolution_clock::now();

    cv::Mat dft_result=convolute_on_frequency_domain(image);

	auto t2 = std::chrono::high_resolution_clock::now();
	auto int_us = std::chrono::duration_cast<std::chrono::microseconds>(t2 - t1);
    cv::normalize(dft_result,dft_result, 0, 1, cv::NORM_MINMAX);
    printf("Time cost(DFT):%dus\n", int_us);

    cv::Mat space_result;

	auto t3 = std::chrono::high_resolution_clock::now();
    cv::filter2D(image,space_result, CV_8U, kernel);
	auto t4 = std::chrono::high_resolution_clock::now();

	auto int_us2 = std::chrono::duration_cast<std::chrono::microseconds>(t4 - t3);

    printf("Time cost(Space):%dus\n", int_us2);
    
    cv::imshow("Image", image);
    cv::imshow("DFT Output",dft_result);
    cv::imshow("Space Output",space_result);
    
    cv::waitKey(0);
    return 0;
}

3. 輸出結果

可以看到輸出結果，在頻域下摺積的影像顏色對比度較強，但是平滑化效果和在空間域下摺積的效果差不多。在效能上，一個21x21大小的平均濾波核，在頻域內摺積比在空間域摺積節省的接近4ms。一個21x21大小的高通濾波核，在頻域內摺積比在空間域摺積節省的接近6.7ms。

1) 平均濾波

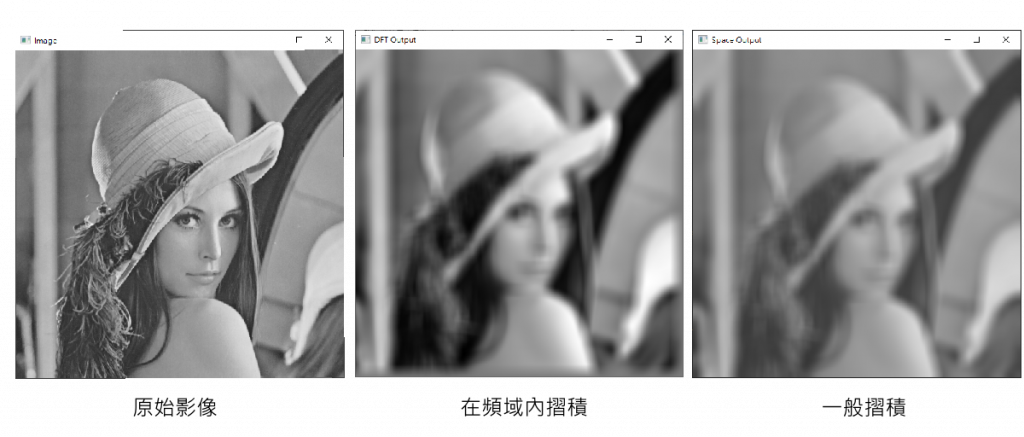
Time cost(DFT):13809us
Time cost(Space):17740us

2) 高斯濾波

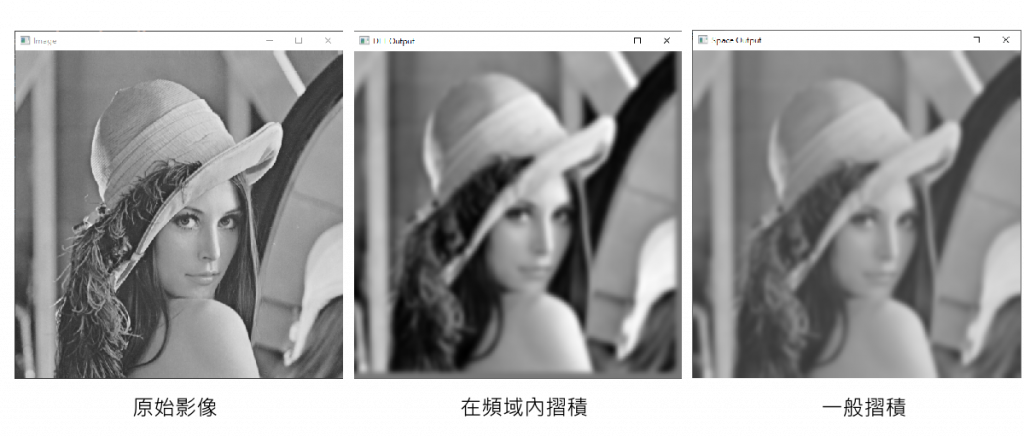
Time cost(DFT):10848us
Time cost(Space):17626us