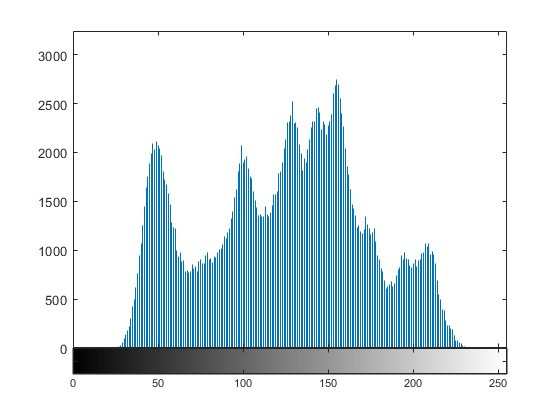
直方圖是用來描述一幅影像中各個灰階值出現頻率的統計圖表。影像的每個像素都有一個對應的灰階值,而直方圖顯示了不同灰階值在整個影像中的分佈情況。直方圖的橫軸代表灰階值,而縱軸則表示該灰階值在影像中出現的次數或像素數量。
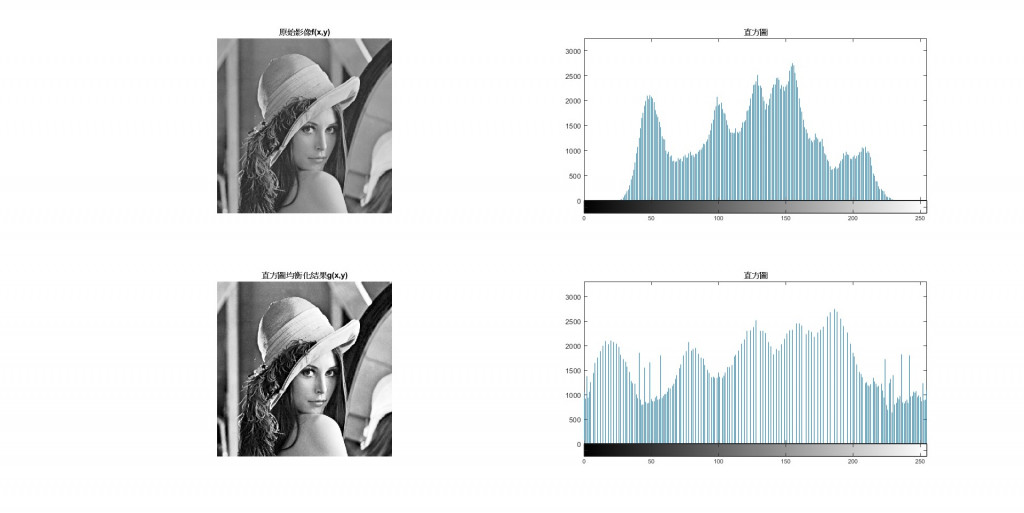
而直方圖均衡化是一種影像處理技術,用於改善影像的對比度和亮度分佈。它是一種強度轉換方法,通過重新分配像素的亮度值,使得影像的亮度分佈變得均勻,從而增強影像的視覺效果。這是通過將原始影像的直方圖轉換成一個均勻分佈的直方圖,從而實現亮度的均衡化。
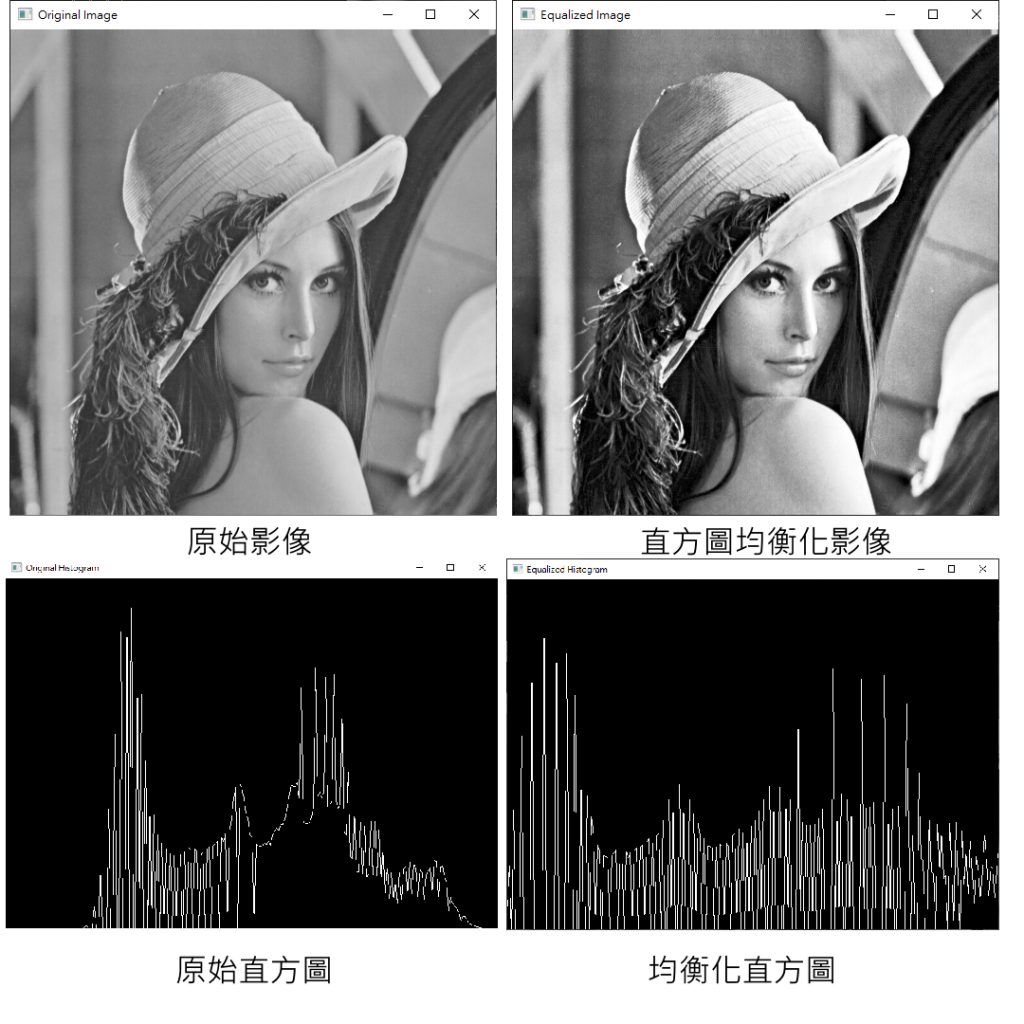
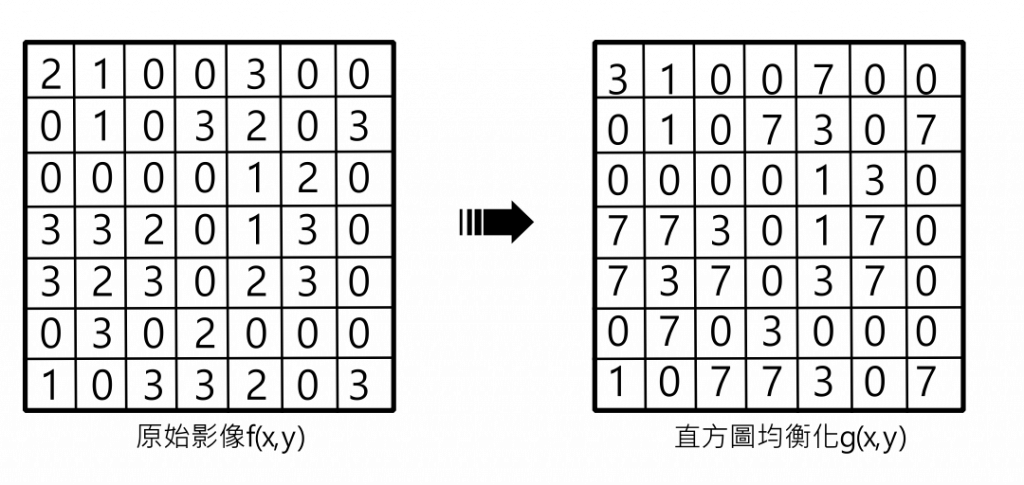
下圖展示經過直方圖均衡化對於影像處理的效果
這個視覺化的展示幫助我們理解直方圖均衡化如何影響影像的對比度和整體外觀,以及如何使影像的像素值更加均勻地分佈在不同的強度範圍中。
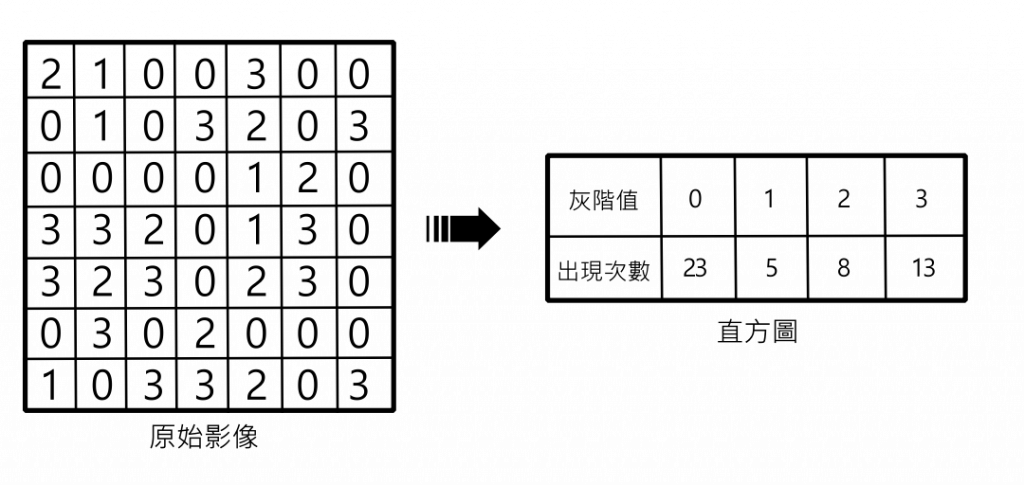
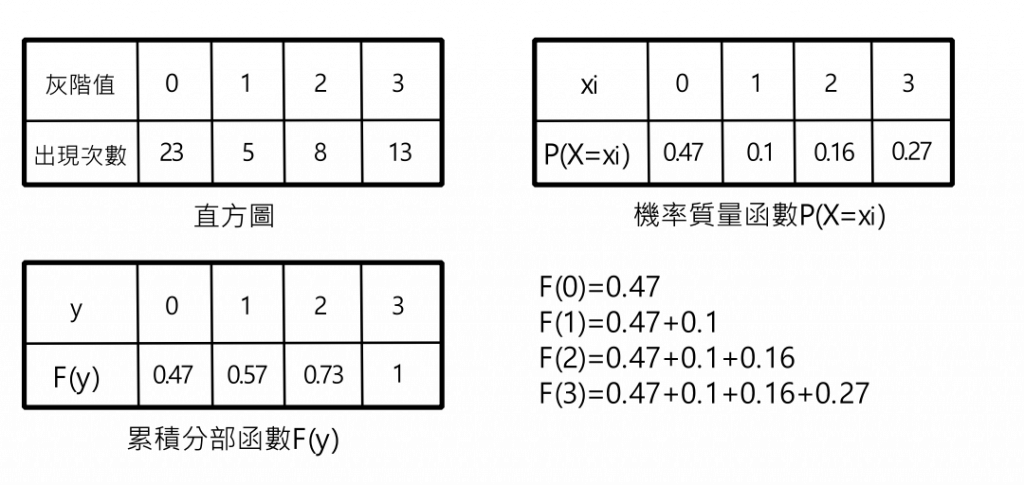
直方圖以柱狀圖的形式呈現,其中每個灰階值對應一根柱子,柱子的高度代表該灰階值在影像中出現的頻率。可以看到下圖圖例,右邊的表格第二行記載了每個灰階值在這張灰階圖片中出現了幾次。
PMF(Probability Mass Function)是概率質量函數的簡稱,用於描述離散型隨機變量的概率分佈。PMF定義了每個可能的取值與其對應的概率之間的關係。它告訴我們每個可能的取值在隨機變數中出現的概率。
在數學上,對於一個離散型隨機變數X,PMF可以表示為: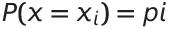
PMF在直方圖的運用上其實概念很簡單,由上個圖例的值方圖可以知道每個灰階值出現在這張圖的次數,也就是說透過特定灰階值出現的次數除以這張圖片的總像素,就是這個灰階值在這張圖片出現的機率值,稱他為這個灰階值在這張圖片上的機率質量函數。你也可以把這個過程想成正規化,把0~255的灰階值重新導向到0~1。
以上面直方圖為例,灰階值0在這張圖片出現23次,這張圖片為7X7大小,所以有49個像素,則23/49就是在這張圖片出現灰階值0的機率。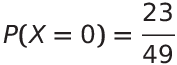
此外,當你把所有的機率質量函數加總起來,就會是1,達到正規化的目的。
累積分布函數(CDF),全稱Cumulative Distribution Function,是用來描述一個隨機變數的機率分佈的數學函數。它給出了這個隨機變數小於或等於一個特定值的加總概率。簡單來說,CDF告訴我們在某個值之前累積出現的概率。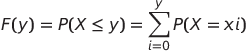
用這個數學是可能比較不好看懂,我們透過下圖的圖例來解釋,看下來其實也很簡單,你只要把小於等於y的機率質量函數做加總,就會得到累積分部函數,而因為機率質量函數有經過正規化,累積分部函數的最後一個數值一定是1。
講解了那麼多機率的的概念,接下來要進入到我們的正題,直方圖均衡化(Histogram Equalization)。
這個公式的作用是將灰階圖像中每個像素的灰階值轉換為0到L-1之間的範圍內的值,使圖片的灰階值更平均。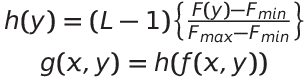
舉上面直方圖的例子,假設灰階的深度只有3位元,也就是只有8個可灰階值可供表示;最大的累計分部函數值為1;最小的累計分部函數值為0.47,則可以列出下列公式: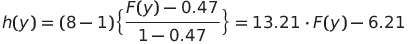
接下來將直方圖的所有灰階值y帶入到上述的公式,就會得到下表,h(y)就是經過直方圖均衡化的結果,可以看到灰階值被重新分布到一個新的灰階值,且灰階值的分布也平均的被分配到了0~7。但要注意,因為我們的原始圖像是3位元的深度,不能儲存浮點數,所以須將輸出的結果四捨五入得到整數值。
| 原始灰階值y | 累計分部函數 F(y) | 均衡化後灰階值 h(y) |
|---|---|---|
| 0 | 0.47 | 0 |
| 1 | 0.57 | 1.32 |
| 2 | 0.73 | 3.43 |
| 3 | 1 | 7 |
最後,將舊的灰階值取代為新的灰階值,就完成直方圖均衡化了。
這個程式碼提供了兩種運算方式,一個是使用OpenCV內建的函式,另一個是使用蜂巢迴圈實現的演算法,兩者效果一樣。你可以透過設定USE_OPENCV 成1或0來決定你要使用前者還是後者的實現方式。
#define USE_OPENCV 1
計算影像陣列的直方圖。
cv::calcHist(&grayImage, 1, 0, cv::Mat(), hist,1, &histSize, histRange, true, true);
images:原始圖像陣列,具有相同的深度和大小,且可以有多個通道。nimages:原始圖像數量(1張)。channels: 計算直方圖的通道(0表示灰階)。mask:可選的遮罩,指定要計算直方圖的元素。這裡使用空白遮罩。hist:輸出的直方圖陣列。dims:直方圖維度(1維)。histSize:每個維度的直方圖的大小,灰階8-bits為256。ranges:每個維度的直方圖灰階值的範圍,灰階8-bits為0~256。uniform:標誌,指示直方圖是否均勻。accumulate:如果設置了這個標誌,在分配直方圖時,它在開始時不會被清除。這個功能使你能夠從多個數組集合中計算一個單一的直方圖,或者隨著時間更新直方圖。非常的簡單,將 grayImage(原始灰階圖像)進行直方圖均衡化,並將結果存儲在 equalizedImage 中。
cv::equalizeHist(grayImage, equalizedImage);
equalizedImage 存儲均衡化後的結果。original_hist,用於存儲原始圖像的像素值直方圖。這個矩陣的每個元素代表對應的像素值出現的次數。(y, x) 獲取灰階值。level 的直方圖計數增加1。equalizedImage = cv::Mat(grayImage.rows, grayImage.cols, grayImage.type());
original_hist= cv::Mat::zeros(256,1,CV_32F);
for (int y = 0;y < grayImage.rows;y++) {
for (int x = 0;x < grayImage.cols;x++) {
uchar level=grayImage.at<uchar>(y, x);
original_hist.at<float>(level) += 1;
}
}
equalizedImage 。float total_pixels = grayImage.rows * grayImage.cols;
cv::Mat pmf = original_hist / total_pixels;
cv::Mat cdf =cv::Mat::zeros(256,1,CV_32F);
float cdf_min=0.0f;
float cdf_max=1.0f;
for (int i = 0;i < pmf.rows;i++){
cdf.at<float>(i) = pmf.at<float>(i) + cdf.at<float>(max(i - 1, 0));
if (cdf_min == 0.0f&&cdf.at<float>(i) > 0.0f) {
cdf_min = cdf.at<float>(i);
}
if (cdf.at<float>(i) > cdf_max) {
cdf_max = cdf.at<float>(i);
}
}
int L = 256;
for (int y = 0;y < grayImage.rows;y++) {
for (int x = 0;x < grayImage.cols;x++) {
uchar level=grayImage.at<uchar>(y, x);
float cdf_y = cdf.at<float>(level);
equalizedImage.at<uchar>(y, x) =((uchar)(L-1) * (cdf_y - cdf_min)/(cdf_max-cdf_min));
}
}
#include <iostream>
#include "math.h"
#include "opencv2/opencv.hpp"
#include "opencv2/core/utils/logger.hpp"
#define USE_OPENCV 1
using namespace std;
void showHistogramWindow(const char* windowName, cv::Mat hist) {
int hist_w = 720, hist_h = 512;
int bin_w = cvRound( (double) hist_w/hist.rows);
cv::Mat histImage=cv::Mat::zeros(hist_h, hist_w, CV_8UC1);
cv::normalize(hist, hist, 0, histImage.rows, cv::NORM_MINMAX);
for( int i = 1; i < hist.rows; i++ )
{
cv::line(histImage,
cv::Point(bin_w*(i-1), hist_h -cvRound(hist.at<float>(i-1)) ),
cv::Point(bin_w*(i), hist_h - cvRound(hist.at<float>(i)) ),
cv::Scalar( 255, 255, 255));
}
cv::imshow(windowName, histImage);
}
cv::Mat calcHist(cv::Mat grayImage) {
cv::Mat hist;
int histSize = 256;
float range[] = { 0, 256 };
const float* histRange[] = { range };
cv::calcHist(&grayImage, 1, 0, cv::Mat(), hist,1, &histSize, histRange, true, true);
return hist;
}
int main()
{
cv::utils::logging::setLogLevel(cv::utils::logging::LOG_LEVEL_ERROR);
cv::Mat grayImage = cv::imread("C:\\Users\\vince\\Downloads\\Lenna.png",cv::IMREAD_GRAYSCALE);
cv::Mat equalizedImage;
cv::Mat original_hist;
cv::Mat dst_hist;
#if USE_OPENCV
original_hist = calcHist(grayImage);
cv::equalizeHist(grayImage, equalizedImage);
#else
equalizedImage = cv::Mat(grayImage.rows, grayImage.cols, grayImage.type());
original_hist= cv::Mat::zeros(256,1,CV_32F);
for (int y = 0;y < grayImage.rows;y++) {
for (int x = 0;x < grayImage.cols;x++) {
uchar level=grayImage.at<uchar>(y, x);
original_hist.at<float>(level) += 1;
}
}
float total_pixels = grayImage.rows * grayImage.cols;
cv::Mat pmf = original_hist / total_pixels;
cv::Mat cdf =cv::Mat::zeros(256,1,CV_32F);
float cdf_min=0.0f;
float cdf_max=1.0f;
for (int i = 0;i < pmf.rows;i++){
cdf.at<float>(i) = pmf.at<float>(i) + cdf.at<float>(max(i - 1, 0));
if (cdf_min == 0.0f&&cdf.at<float>(i) > 0.0f) {
cdf_min = cdf.at<float>(i);
}
if (cdf.at<float>(i) > cdf_max) {
cdf_max = cdf.at<float>(i);
}
}
int L = 256;
for (int y = 0;y < grayImage.rows;y++) {
for (int x = 0;x < grayImage.cols;x++) {
uchar level=grayImage.at<uchar>(y, x);
float cdf_y = cdf.at<float>(level);
equalizedImage.at<uchar>(y, x) =((uchar)(L-1) * (cdf_y - cdf_min)/(cdf_max-cdf_min));
}
}
#endif
showHistogramWindow("Original Histogram",original_hist);
dst_hist = calcHist(equalizedImage);
showHistogramWindow("Equalized Histogram",dst_hist);
cv::namedWindow("Original Image", cv::WINDOW_AUTOSIZE);
cv::imshow("Original Image", grayImage);
cv::namedWindow("Equalized Image", cv::WINDOW_AUTOSIZE);
cv::imshow("Equalized Image", equalizedImage);
cv::waitKey(0);
return 0;
}
原始圖像通常可能因光線變化、曝光不足等原因導致部分區域的細節不易辨識,對比度不高。可以看到,在經過直方圖均衡化後,圖像的像素值重新分佈,使灰階值在整個像素值範圍內均勻分布,同時提高整體的對比度,但當然,雜訊也會更明顯。