接續昨天的「十進位」和「二進位」的轉換，今天這篇會以例子的方式來探討「十六進位」和「二進位」的互換。如果你對進位法還不是很了解，可以參考之前的文章電腦的魔法語言 - 探索二進制世界的奧秘

「二進位」轉「十六進位」

在正式進入進位法的轉之前，先來了解十六進位是什麼
十六進位是指以基數 16 的運算系統，由 0 ~ 9 和大寫字母A ~ F組成。十六進位的值會對應十進位的 0 ~ 15(共 16 個數字)，例如 A = 10, F = 15，可以直接看下圖：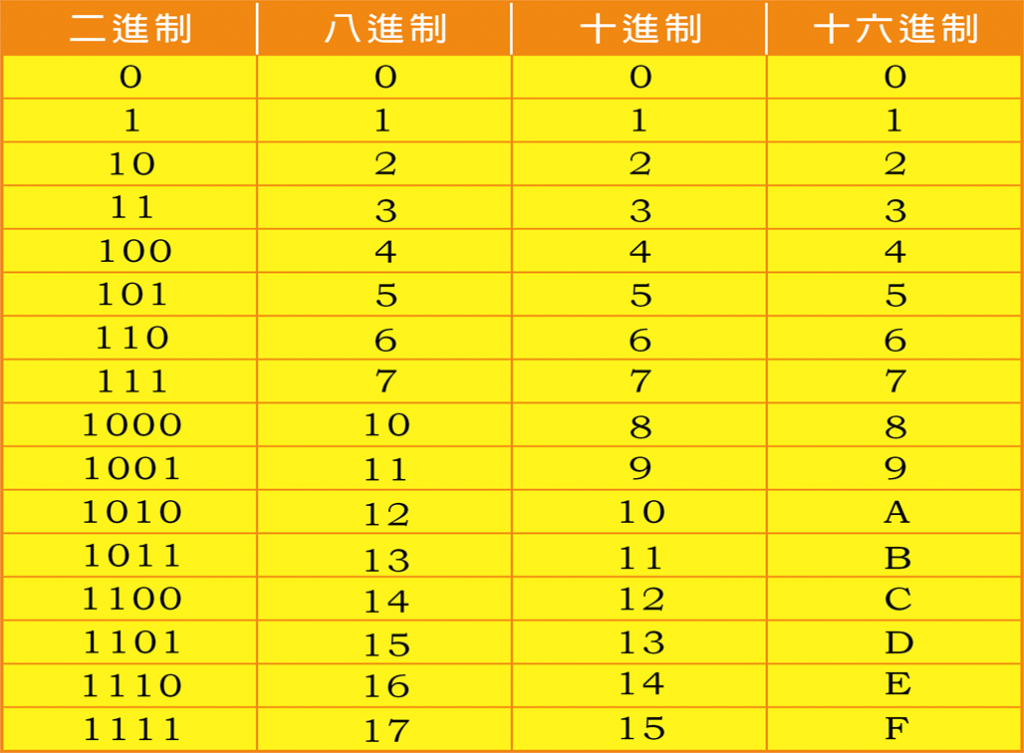

因為 16 為 2 的整數次方，所以二進位數和十六進位數可說是戲出同門啦～ 他們之間的轉換也比較簡單

PS 補充：「十進位」轉「十六進位」可以想成 不斷地 ÷ 16，跟「十進位」轉「二進位」一樣，只是基數從 2 轉為 16而已

可以拆為「整數部分」和「小數部分」來執行
STEP1: 將「整數部分」分組，從小數點往'左'每 4 個位元一組，並換成16進位
STEP2: 將「小數部分」分組，從小數點往'右'每 4 個位元一組，並換成16進位
STEP3: 將上述兩步驟結果合併

範例一： 110110101.11011 轉換為「十六進位」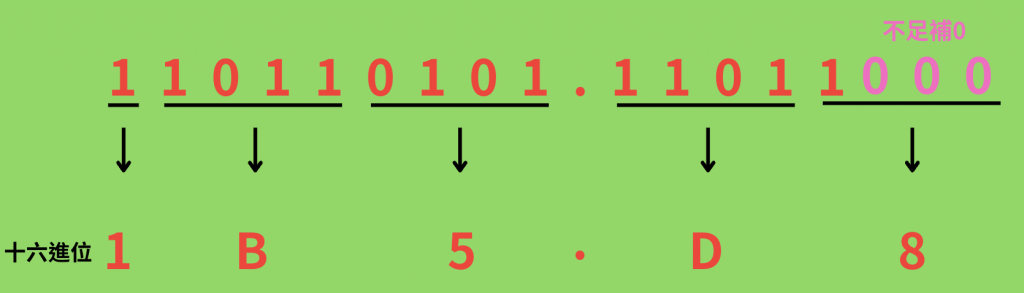

STEP1: 將「整數部分」從小數點往左開始分組，得到 1_1011_0101，換為十六進位為 1B5 (為了易讀，每四位用底線隔開)
STEP2: 將「小數部分」從洗數點往右開始分組，得到 1101_1，換為十六進位為 D8
STEP3: 最後的結果為 1B5.D8

「十六進位」轉「二進位」

範例一： 把剛剛上面的 1B5.D8 轉換為「二進位」，
一樣可以拆為「整數部分」和「小數部分」來執行
STEP1: 整數部分為 1B5.D8 ，先把 B, D 轉成「十進位」，B = 11; D = 13
STEP2: STEP1換成十進位後，就可以再繼續將「十進位」換成「二進位」，整數和小數一樣分開算

把上面的步驟變成下面這張圖，有些轉換的計算因怕版面過於雜亂，所以就沒加上了
圖畫得沒有很好請見諒！！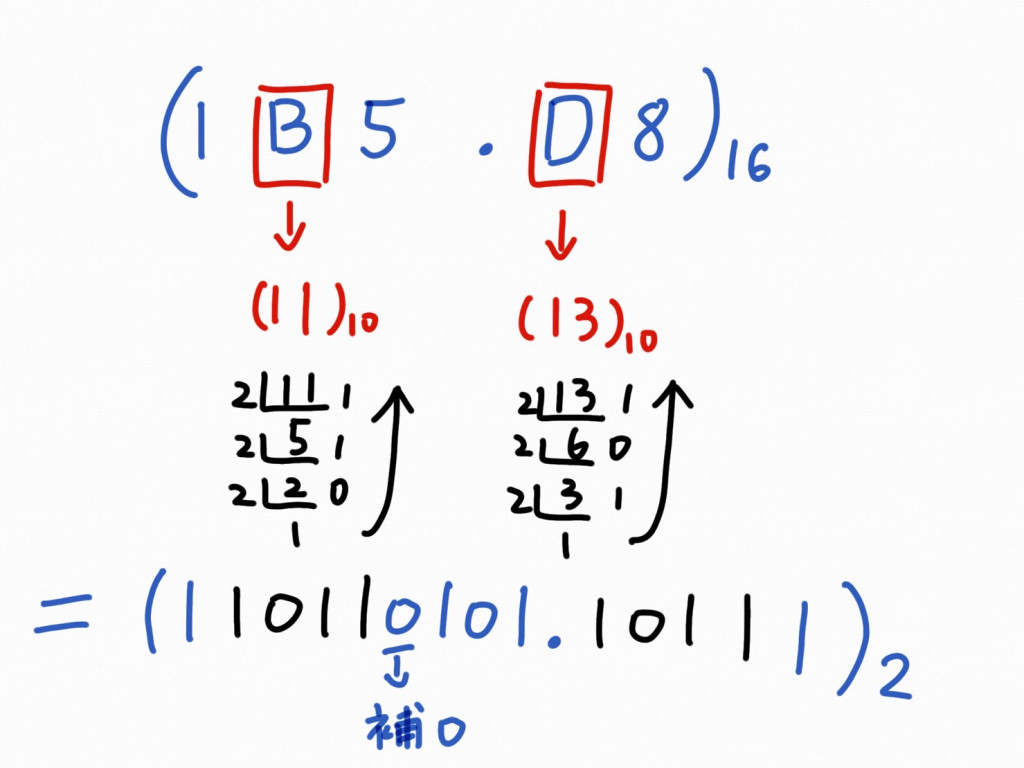

這題答案就是 1_1011_0101.1101_1 5 (為了易讀，每四位用底線隔開)

PS 轉換器：https://tools.yeecord.com/calculator/dec/bin

總結

各種進位法之間所要表達的總數都是一樣的，只是表示方式不一樣，就像下圖中的 12 顆蘋果

如果換成各進位法如下：

十進位: 12
二進位: 1100
十六進位: C

透過例子學習是比較快的方式，希望今天的內容能對你有所幫助，部分圖片因版面關係，所以省略掉了一些計算，有問題也可以在下方討論

參考資料

1. wikipedia
2. 全華 - 計算機概論 資訊素養大補帖