238. Product of Array Except Self

解題程式碼

var productExceptSelf = function (nums) {
  const result = [];
  let right = 1;
  result[0] = 1;

  for (let i = 1; i < nums.length; i++) {
    result[i] = result[i - 1] * nums[i - 1];
  }

  for (let i = nums.length - 1; i >= 0; i--) {
    result[i] = right * result[i];
    right = right * nums[i];
  }

  return result;
};

解題思路、演算法

這題的題目有限制: 時間複雜度須是 O(n) 並且沒有使用到除法，Follow up 還有一個條件是，output 陣列不納入計算的話，空間複雜度為 O(1)，所以這題無法使用"將所有 input 陣列元素都先相乘後得出總合，再對各個元素除法後得出 except self 的總和"。

所以觀看他人解法，得知:

1. 陣列中的一個數，其結果會是左半邊的所有值相乘後，再乘上右半邊的所有值相乘，例如 [1,2,3,4] 中的 3 在結果陣列的對應位置會是 8，因為 1 _ 2(左半邊) _ 4(右半邊) = 8
2. 先從左到右遍歷一次，去記錄累乘結果，res[i] = res[i - 1] * nums[i - 1]

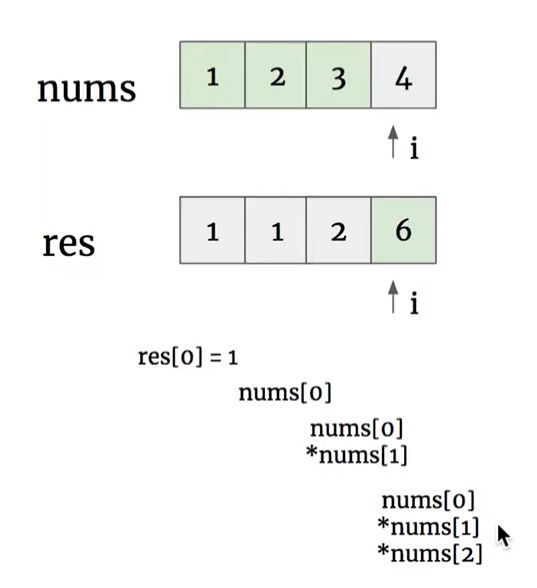
3. 再從右到左遍歷一次，去記錄累乘結果，res[i] = res[i] * right

解法的時間、空間複雜度

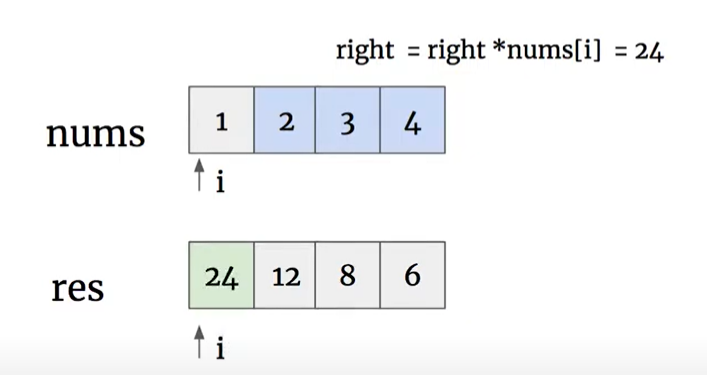
時間複雜度: O(n)
空間複雜度: O(n)，output array 不算則是 O(1)

參考資料

Product of Array Except Self - Leetcode 238 - Python

[LeetCode]238. Product of Array Except Self 中文

39. Combination Sum

解題程式碼

var combinationSum = function (candidates, target) {
  const result = [];

  const tracking = (tempList, curSum, index) => {
    if (curSum === target) {
      result.push([...tempList]);
      return;
    }

    // 解法 1
    // if (curSum > target) return;
    // for (let i = index; i < candidates.length; i++) {
    //     tempList.push(candidates[i]);
    //     tracking(tempList, curSum + candidates[i], i);
    //     tempList.pop();
    // }
    // 解法 1-----------

    // 解法2-----------
    if (index >= candidates.length || curSum > target) return;
    tempList.push(candidates[index]);
    tracking(tempList, curSum + candidates[index], index);
    tempList.pop();
    tracking(tempList, curSum, index + 1);
    // 解法2-----------
  };
  tracking([], 0, 0);

  return result;
};

解題思路、演算法

這題可以使用回溯法處理，回溯法是一種找出問題所有解的演算法，常用遞迴的方式去窮舉各種結果的數值，一旦發現窮舉到和結果要求不符合的數值，就停止往下層窮舉下去，省去繼續往下探索的時間

一個數字只會有兩種情形，選或者不選，而且題目有提到一個數字可以重複選，所以題目的 Example 1 我們可以畫成如下圖，並分成三種情況選數字:

1. 拿現在遍歷的數字，下一次再拿現在遍歷的數字
2. 拿現在遍歷的數字，下一次拿陣列內的下一個數字
3. 不拿現在遍歷的數字，下一次拿陣列內的下一個數字

如果總和超過 target value，該分支就不再搜尋下去。

解法的時間、空間複雜度

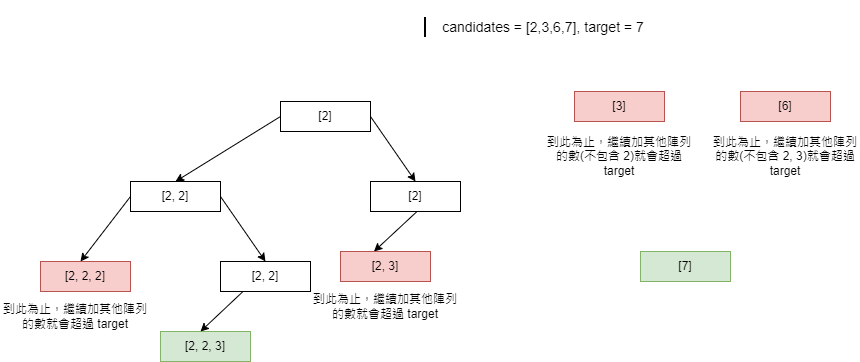
時間複雜度: O(N^(T/M)+1), N: # of candidates; T: target value; M: minimum number in candidates，相當於 dfs 遍歷一個高度為 T/M 的 N-ary tree，節點個數為 N^(T/M)+1
空間複雜度: O(2^T)

參考資料

leetcode 中文 | LeetCode 39. Combination Sum - Python 思路總結

Combination Sum - Backtracking - Leetcode 39 - Python

五大基本算法之回溯算法 backtracking

56. Merge Intervals

解題程式碼

var merge = function(intervals) {
    const out = [];
    intervals = intervals.sort((a, b) => a[0] - b[0]);
    let curInterval = intervals[0];

    for(let i = 1; i < intervals.length; i++) {
        if (curInterval[1] >= intervals[i][0]) {
            curInterval = [Math.min(curInterval[0], intervals[i][0]), Math.max(curInterval[1], intervals[i][1])];
        } else {
            out.push(curInterval);
            curInterval = intervals[i];
        }
    }
    out.push(curInterval);

    return out;
};

解題思路、演算法

這題如果先做過 57. Insert Interval 就很好想出怎麼寫了。

一開始先做排序(如果實際面試可以詢問是否 input 有先排序!?)，之後在做值的比較會比較好處理。

然後用 curInterval 變數記錄當前的區間，接著去遍歷整個 intervals，分成兩個情況來處理:

• 有重疊，就合併當前遍歷的 intervals[i] 陣列和 curInterval，將合併後的值更新到 curInterval
• 沒重疊，就加入最終結果陣列 out，更新 curInterval 為當前遍歷到的 intervals[i]

解法的時間、空間複雜度

時間複雜度: O(n * log n)
空間複雜度: O(n)

參考資料