今天要來分享的是利用了Greedy策略去解決在資料結構中的Graph上某個節點到其餘的節點的最短路徑問題，其中的經典演算法：Dijkstra's Algorithm。
這個演算法需要對Graph和Heap這兩個資料結構有一些認識才比較好理解：）
那我們就開始吧。

Dijkstra's Algorithm 分析

敘述：如果有五個城市分別命名為A~E，如圖所示，我們想從城市Ｃ以最短的路徑到達其他城市。請輸出到達個城市的最短距離。

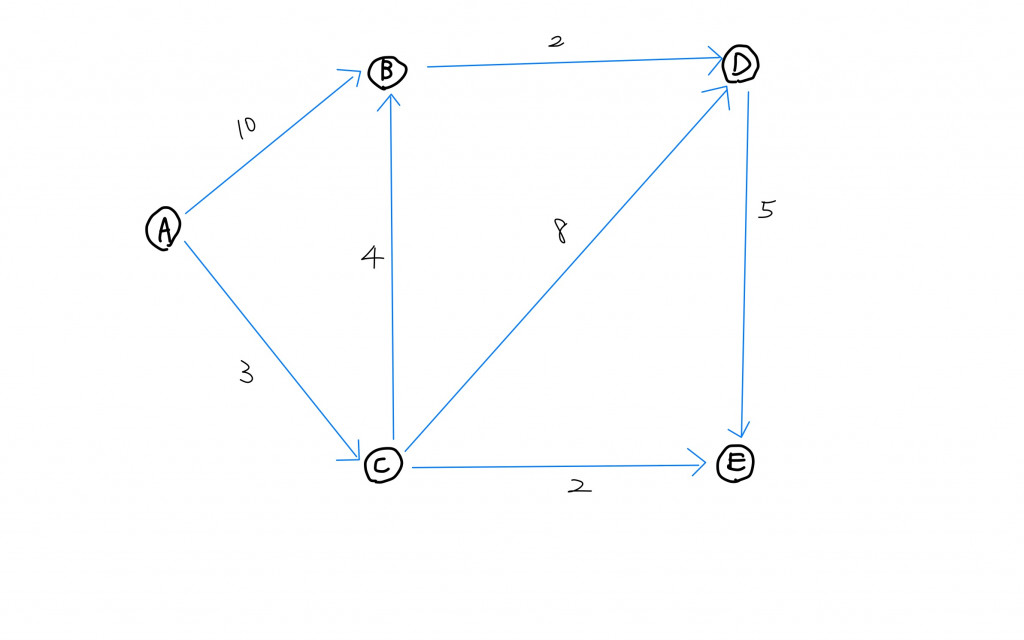
分析：我們打算以greedy的策略去解決這個問題，「永遠都先挑從該節點到達另一個節點的最短累積距離」，其餘的則儲存起來。要以程式碼實作出上述的需求，有一個資料結構非常符合，那就是minimum heap。

為什麼 「永遠都先挑從該節點到達另一個節點的最短累積距離」

起點C共有3條路徑可以走，他們一開始都會被存放到heap中，其中C到E擁有最短的距離所以會被pop出來，我們確信這就是C到E的最短距離所以把他紀錄下來。 接著再將E可以到達別的節點的距離「加上」C到達E的最短距離存放到heap中，因為我們的目標是C到個點的最短距離，所以需要累加。

另外，如果認為C到E有其他更短的距離，所以不應該直接確信當下從heap pop出來的C到E的距離為最短距離就會產生矛盾。因為C到B的距離以及C到D的距離都已經比C到E的距離長了，不可能再走其他節點的路徑到達E會有比C到Ｅ更短的距離了。所以這個greedy策略是可行的。同時這也帶出了這個演算法的限制，「Dijkstra's Algorithm 不可以有negative weight」。

程式實作

1. 首先我們要將圖轉換成Adjacent List去保存
2. 我們需要一個minimum heap在一開始存放[初始距離(0)，起點]這個pair，在python呼叫minimum heap很簡單，只要import heapq就搞定了～
3. 利用回圈去計算到達各個node的最短距離，終止條件為heap變成空的

import heapq

def shortestPath(edges, n, src):
    adj = {}
    for i in range(1, n + 1):
        adj[i] = []

    # s = src, d = dst, w = weight
    for s, d, w in edges:
        adj[s].append([d, w])

    shortest = {}
    minHeap = [[0, src]]
    while minHeap:
        w1, n1 = heapq.heappop(minHeap)
        if n1 in shortest:
            continue
        shortest[n1] = w1

        for n2, w2 in adj[n1]:
            if n2 not in shortest:
                heapq.heappush(minHeap, [w1 + w2, n2])
    return shortest

Question1

為什麼要有：

if n1 in shortest:
    continue

ans:
因為我們是以greedy的策略的解題，所以先被pop出來的節點和距離就是起點到達該節點的最短距離了。再pop出來一樣的節點的距離就應該忽略。

Question2

為什麼要有：

if n2 not in shortest:
    heapq.heappush(minHeap, [w1 + w2, n2])

ans:
如果某個節點已經被記錄過起點到該節點的最短距離了，還是有可能因為有其他節點可以到達這個節點而再次出現，為了加速運算速度：我們的終止條件是heap變成空，所以需要設立條件去filter。

Time Complexity

分析：worst case是所有的節點間連向除了自己以外所有的節點：這樣會有E條路徑被push到heap中。不管是push或是pop，heap的運算都是logn，所以複雜度為O(ElogE)。

我們可以學到什麼

1. 了解Dijkstra's Algorithm的概念
2. 程式實作的pattern，leetcode有很多題目都可以利用類似的pattern來解題

# preprocess with graph
# ...

#initiate a heap
h = []
heapq.heappush(h, (0, src))

while h:
    dis, node = heapq.heappop(h)
    # ...

Leetcode 743. Network Delay Time

敘述：

1. 在網路上有n個節點，以1到n去標記
2. 從某個節點到另外一個節點需要花費時間，以(u, v, w)去紀錄，即節點u到節點v需要花費w
3. 如果從某一個節點發送信號，這個信號傳給所有節點最少要花費多少時間
4. 如果無法傳送給所有節點則回傳-1

Example: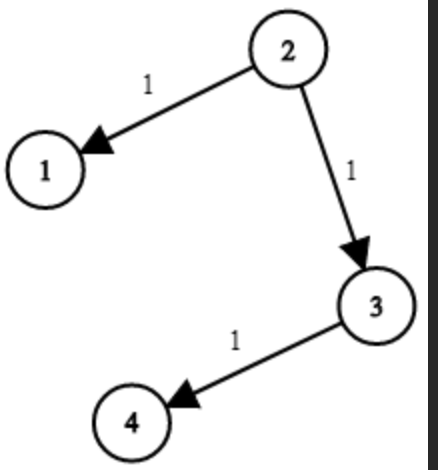

Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
Output: 2

分析：

1. 看到graph, minimum、從某節點到達另一個節點，我們可以試試看greedy策略跟上面的模板
2. 我們還需要一個set去紀錄已經到達過的節點有哪些，避免重複拜訪
3. 現在我們開始去對graph去做前處理，把它轉化成adjacent list
4. 初始化heap，並且存放(到達這個節點要花的時間，節點編號），即(0, k)
5. 在迴圈中，我們要「一口氣將到達時間一樣的節點」都pop出來，代表訊號是同時抵達這些節點的
6. 而這些節點所連接且未被拜訪過的節點，信好抵達的時間為目前累積的時間＋從source到達該節點所需時間

class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        cost = 0
        adjList = defaultdict(list)
        for src, dst, t in times:
            adjList[src].append((dst, t))
        
        h = [(0, k)]
        visit = set()

        while h:
            curTime, node = h[0][0], h[0][1]
            if node in visit:
                heapq.heappop(h)
                continue
            cost = curTime

            while h and h[0][0] == curTime:
                t, nextSrc = heapq.heappop(h)
                visit.add(nextSrc)

                for dst, time in adjList[nextSrc]:
                    if dst not in visit:
                        heapq.heappush(h, (t + time, dst))

        return cost if len(visit) == n else -1

謝謝大家觀看，明天中秋節繼續更新（太血汗啦 ＼(´◓Д◔`)／）