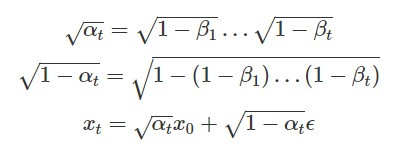在 [Day 18] 淺談 Diffusion Model 的演算法我們留下了兩個疑問：

1. 為什麼在加 noise 的過程（forward process）中，noise 不是一個 step 一個 step 加到影像上，而是一步加到位？
2. 為什麼在生成影像的過程中每次 denoise 後還要再加上 noise？

在今天的文章中，會先解釋第一個疑問，其實一步一步加 noise 的效果，是可以用加一次 noise 等效的！而這部分的內容主要參考李宏毅老師的公開線上課程【生成式AI】Diffusion Model 原理剖析 (3/4) (optional)～

首先來談一下一般性的加 noise 過程，當我們要將 t-1 step 的影像 x_(t-1) 加 noise 得到的 t step 的影像 x_t，這個過程 q(x_t|x_(t-1)) 可以表示如下（用貓貓影像為例）：

其中 β_t 這個參數是由人決定的，每個 step 會有不同對應的 β_1、β_2、...、β_T，它會影響 noise 和影像的佔比。

換個角度想，x_t 其實就是從一個 Gaussian distribution 抽樣的結果，而這個 Gaussian distribution 的 mean 是 (1-β_t)^(1/2)x_(t-1)，sigma 就是 β_t^(1/2)。

那我們可以以此類推每個 step 間的轉換過程，例如從乾淨的影像 x_0 加 noise 得到有點 noise 的影像 x_1，和從有點 noise 的影像 x_1 加 noise 得到有更多 noise 的影像 x_2 的過程如下：

接著可以透過變數代換的方式得到 step 2 的影像 x_2 和乾淨的影像 x_0 的關係：

其實就是乾淨的影像 x_0 加了兩次 Gaussian noise，但這兩次加的 noise 可以用一個 Gaussian noise 代換！

最後，我們就可以用同樣的道理類推從乾淨的影像 x_0 到任意 t step 的影像 x_t 的關係：

這也就代表著我們可以在乾淨影像 x_0 上加一個 Gaussian noise 就直接得到任意 step 的有噪聲的影像。

而如果以 α_t 用以下的方式代換，我們就可以得到 paper 訓練演算法中，含有 noise 的影像的數學形式：