今天又是充滿數學的一天啊

還記得在 [Day 19] Diffusion Model 的數學原理（一）的最後，我們得出了 diffusion model 的學習目標：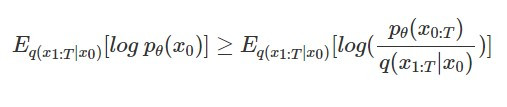

今天我們會從這個學習目標出發，得到最後我們在演算法看到生成過程如何 denoise 的數學形式：

（圖片來源：Denoising Diffusion Probabilistic Models）

那就直接開始吧！

首先，根據 Understanding Diffusion Models: A Unified Perspective 中的推導，我們可以將 diffusion model 要最大化的 lower bound 寫成以下三項：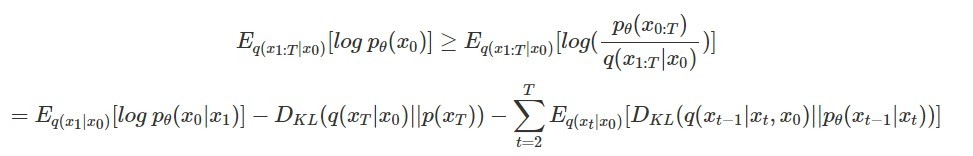

至於中間是如何推導的呢？有興趣的話可以參考這個來自 paper 的截圖，但不看應該也不會影響理解太多：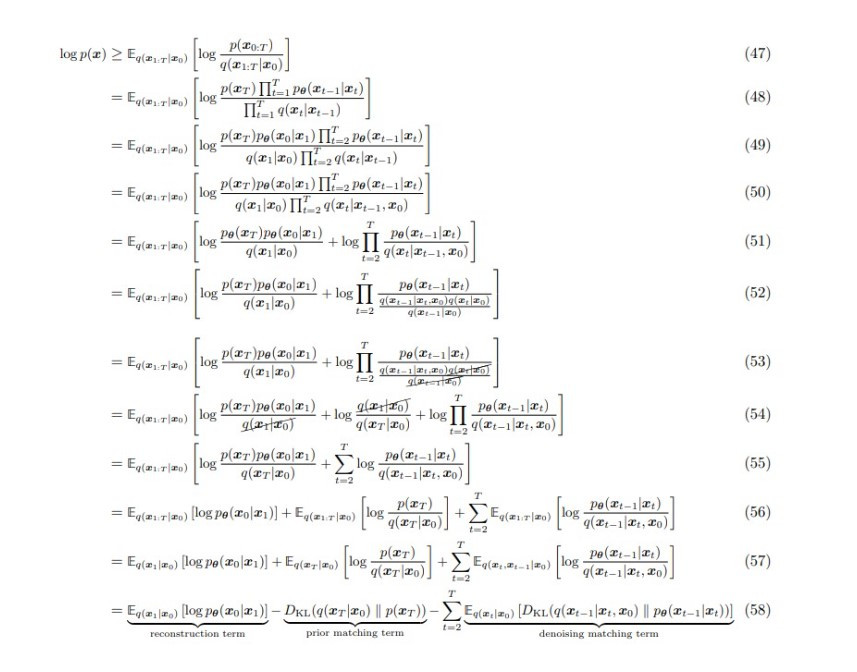

（圖片來源：Understanding Diffusion Models: A Unified Perspective）

那推導出來的這三項分別代表以下的涵義：

1. ：意義接近 VAE 的 reconstruction term，也就是 denoise 後的影像和原本乾淨的影像有多接近
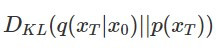2. ：prior matching term，它代表加 noise 的影像最終多接近先驗的 Gaussian distribution，由於加 noise 的部分和模型參數完全無關，因此在後面的計算可以忽略
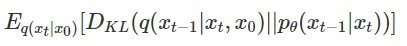3. ：denoising matching term，評估每一步 denoise 的結果和加 noise 前是否接近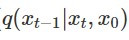，代表的是 ground truth signal，也就是在已知 x_0 和 x_t 的情況下要如何 denoise 得到 x_(t-1)；而 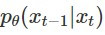則是模型學出來的 denoise 函數

由於和演算法中 denoise 過程有關的是第三項 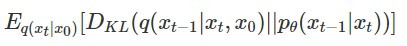，因此接下來會繼續從這一項推導～

其中 ground truth signal 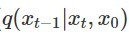經過一連串複雜的推導後，會發現它其實也是一個 Gaussian distribution，mean 是 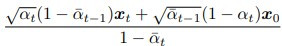，sigma 是 ：

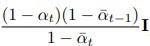（圖片來源：Understanding Diffusion Models: A Unified Perspective）

而 diffusion model 要學出的 denoise 函數 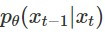也是一個 Gaussian distribution，由於它的 mean 是可以被訓練的，sigma 是固定的，因此要拉近 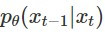和 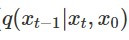兩個機率分布，就是要讓可被訓練的 mean 和 ground truth 的 mean 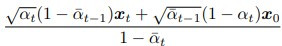越接近越好。

由於我們知道 x_0 和 x_t 的關係：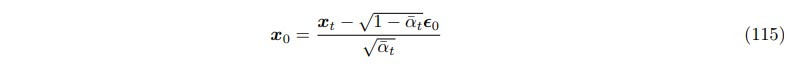

（圖片來源：Understanding Diffusion Models: A Unified Perspective）

我們可以將上面的等式代入 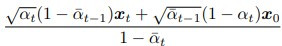，讓它只與 x_t 相關：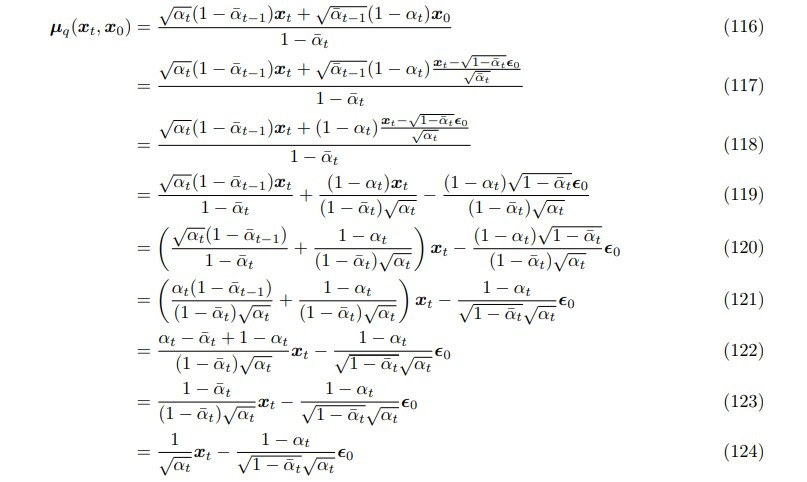

（圖片來源：Understanding Diffusion Models: A Unified Perspective）

最後就得到演算法中 denoise 過程的數學形式 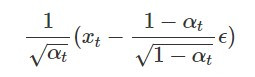了！

不過實際上在 denoise 的時候，我們並不會直接讓模型輸出機率分布最高的值（也就是 Gaussian distribution 的 mean），這樣缺乏隨機性的過程通常反而是對生成結果有害的，取而代之的是我們會從 Gaussian distribution 抽樣，這也就是為什麼演算法中會寫 denoise 過程中還要加上隨機抽樣的 noise：

（圖片來源：Denoising Diffusion Probabilistic Models）